 |
Az S. 32. feladat (2008. január) |
S. 32. Egy nemzeti parkban minden nevezetességhez el lehet jutni kerékpáron is. Egy kemény tél után azonban egyes kerékpárutak megrongálódtak. Minden utat felmértek, és meghatározták annak felújítási értékét, vagyis hogy mennyire lenne fontos azt felújítani.
A park vezetősége úgy döntött, hogy még a nyári csúcsszezon előtt a legfontosabb felújításokat el kell végezni, az viszont nem fordulhat elő, hogy a látogatók a felújítások alatt ne tudjanak minden nevezetességhez kerékpárral is eljutni. Egyszerre tetszőlegesen sok útszakasz újítható fel, ugyanakkor minden útszakasz felújítása az egész tavaszi időszakot igénybe veszi.
Írjunk programot, mely meghatározza, hogy a tavasz során legföljebb hány felújítás végezhető el, és ez alapján mennyi a ténylegesen felújított utak felújítási értékei összegének maximuma.
A program az utak leírását fájlból olvassa, az eredményt fájlba írja. A bemeneti, illetve kimeneti fájlok nevei az első, illetve második parancssori argumentum (az alábbi példában s32 be.txt ki.txt).
A bemenet első sorában egy-egy szóközzel elválasztva a nevezetességek N (legföljebb 100) és az őket összekötő kerékpárutak M (legföljebb 500) száma található. A nevezetességeket az számokkal azonosítjuk. Az ezt követő M sor mindegyike három pozitív egész számot tartalmaz szóközzel elválasztva A B F alakban: egy-egy kerékpárút által (kétirányúan) összekötött nevezetességek A és B sorszámát, valamint annak F>0 felújítási értékét (1 és 1000 közötti egész), illetve F=0, ha az utat nem kell felújítani.
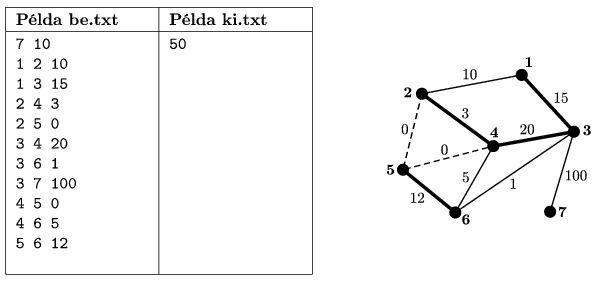
A kimenet egyetlen szám: az optimális felújítás esetén felújított utak felújítási értékeinek összege.
Beküldendő a program forráskódja (s32.pas, s32.cpp, ...), valamint a program rövid dokumentációja (s32.txt, s32.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
A beküldési határidő 2008. február 15-én LEJÁRT.
A feladat megoldása
A feladat hatékony megoldásához azt kellett észrevenni, hogy célszerűbb "visszafelé" dolgozni, azaz nem egy olyan legnagyobb összértékű úthalmazt keresni, melyet elhagyva a teljes úthálózatból az még összefüggő marad, hanem épp ennek komplementerét, azaz az üres úthálózatból kiindulva egy olyan legkisebb értékűt építeni, melyen már el tudunk jutni minden nevezetességhez. Ugyanis így a feladat nem más, mint az úthálózat gráfjában egy minimális költségű feszítő fa keresése, mely probléma megoldására felhasználhatjuk pl. Prim vagy Kruskal algortimusát. Megjegyezzük, hogy a feladat "előrefelé" is megoldható hatékonyan, ehhez azonban az előbbieknél lényegesen bonyolultabb algoritmus(ok), ill. adatstruktúrák szükségesek.
A mintamegoldás Kruskal algoritmusának unió-holvan adatszerkezettel történő megvalósítását mutatja be. Ha az úthálózat éleinek számát e-vel jelöljük, műveletigénye .
Engedy Balázs
Statisztika:
5 dolgozat érkezett. 10 pontot kapott: Szebeni Szilveszter, Véges Márton. 9 pontot kapott: Godó Zita. 8 pontot kapott: 1 versenyző. 5 pontot kapott: 1 versenyző.
A KöMaL 2008. januári informatika feladatai

