Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Az S. 59. feladat (2011. január)

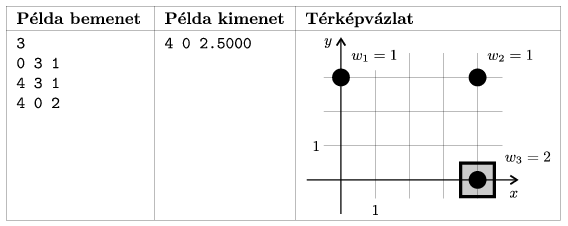
S. 59. Egy befektető Manhattan szívében új luxus bevásárlóközpont építését tervezi. Jól tudja, hogy a legnagyobb látogatottság úgy érhető el, ha a helyszín minél közelebb esik a lehetséges vásárlókhoz.

Ezért részletesen felmérte, hogy a város mely részéből hány vásárlóra lehet számítani, most pedig -- mint legjobb tanácsadóját -- minket kért meg, hogy javasoljunk számára olyan helyszínt, melynek eléréséhez átlagosan a lehető legkevesebbet kell utazniuk a vásárlóknak.

Írjunk programot a feladat megoldására. A megoldás során a hagyományokhoz hűen Manhattan úthálózatát tekintsük egy (kétirányú utakból álló) szabályos rácsnak, melynek kereszteződései az egész koordinátájú pontokban vannak.

Az egyszerűség kedvéért azonosítsuk a hozzájuk legközelebb eső kereszteződéssel mind a bevásárlóközpont, mind a vásárlók lakásainak helyét, a \mathbf{p}_{i}=(x_{i}, y_{i}), \mathbf{p}_{j}=(x_{j}, y_{j}) koordinátájú kereszteződések távolsága pedig rács menti legkisebb távolságuk, azaz a következő legyen:

d(\mathbf{p}_i,\mathbf{p}_j)= |x_j -x_i|+ |y_j -y_i|.

A program a felmérés eredményét a standard bemenetről olvassa. Ennek első sora a felmért kereszteződések 1\le N\le 1\;000\;000 számát tartalmazza, az ezt követő N darab sora pedig egy-egy kereszteződést ír le. Az i+1-edik sorban egy-egy szóközzel elválasztva három egész szám, az i-edik kereszteződés 0\le x_i,y_i \le 1\;000\;000 koordinátái, illetve az onnan várható vásárlók 1\lewi\le1000 száma található.

A fenti jelölésekkel tehát a bevásárlóközpont számára azt az optimális \mathbf{p}_{0} kereszteződést keressük, melytől a felmért kereszteződések -- az egy kereszteződésben lakók számával súlyozott -- átlagos távolsága minimális:

\overline D = \frac{\sum\limits_{i=1}^N d(\mathbf{p}_0,\mathbf{p}_i)\cdot w_i}{\sum\limits_{i=1}^N w_i}, \quad\mbox{ahol}\quad \mathbf{p}_i=(x_i,y_i).

A standard kimenet egyetlen sorába mindössze három, szóközzel elválasztott szám kerüljön: a bevásárlóközpont optimális \mathbf{p}_{0} helyszínének x0, y0 koordinátái, illetve az ehhez tartozó \overline D átlagos távolság, 4 tizedes pontossággal. Több megoldás esetén bármelyik megadható.

Értékelés: a maximális 8 pont eléréséhez a programnak a legnagyobb teszteseteket is egy percen belül meg kell oldania, ugyanakkor már 5 pont szerezhető az N\le1000 feltételnek eleget tevő tesztesetek megoldásával is. További 2 pontot ér a dokumentáció.

Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció (s59.txt, s59.pdf, ...) egy tömörített mappában (s59.zip).

(10 pont)

A beküldési határidő 2011. február 10-én LEJÁRT.

Megoldásvázlat

A megoldáshoz azt kellett észrevenni, hogy az átlagos távolság épp akkor minimális, amikor a súlyozott távolságösszeg minimális (hisz egymás konstansszorosai), ennek pedig függőleges és vízszintes összetevői egymástól teljesen függetlenek, így külön-külön minimalizálhatóak.

Tehát két egydimenziós problémát kaptunk: két, abszolútérték-függvények összegeiből felépített függvény minimumhelyét kell meghatároznunk. Az ilyen függvények konvexek, és egyenes szakaszokra bonthatóak: minimumhelyük tehát ott van, ahol ezen szakaszok meredeksége negatívból pozitívba fordul, amely egy rendezés után lineáris időben meghatározható.

C++ mintamegoldás

Statisztika:

8 dolgozat érkezett.
10 pontot kapott:Borsos 607 Zalán, Nagy 111 Miklós, Szabó 928 Attila.
9 pontot kapott:Nagy Róbert.
8 pontot kapott:1 versenyző.
7 pontot kapott:1 versenyző.
5 pontot kapott:1 versenyző.
4 pontot kapott:1 versenyző.

A KöMaL 2011. januári informatika feladatai