 Problem S. 77. (January 2013)
Problem S. 77. (January 2013)
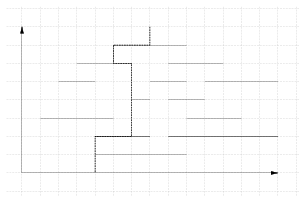
S. 77. Your robot has to navigate through an obstacle course: the goal is to reach the x-axis as soon as possible. However, there are several obstacles on the board, represented as horizontal line segments (without having any thickness in the y-direction) blocking the robot's way: the robot cannot pass through these. The movement of the robot is always parallel to the axes.
Your program should determine the length of the shortest path of the robot reaching the x-axis, provided that the initial position of the robot and the positions of the endpoints of the obstacles are known.
Input: The first line of the standard input contains the number of obstacles (), while the second line contains the x and y coordinates of the initial position of the robot, separated by a space. Then each of the following N lines describes an obstacle by 3 numbers (separated by a space): the first giving the y coordinate of the actual line segment, while the next two numbers specifying the x coordinates of its endpoints. All coordinates are positive integers below 1000000. Obstacles are disjoint and their length cannot be 0.
Output: The single line of the standard output should contain the length of the shortest path.
In the examples below (``Példák''), some input-output (``Bemenet-Kimenet'') pairs are shown.
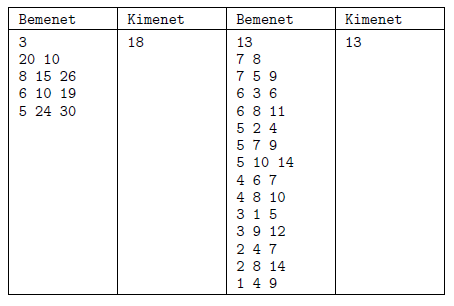
Scoring: You can obtain 2 points for a brief and proper documentation clearly describing your solution. The maximal 8 points for your program can only be obtained if it can solve an arbitrary valid input within 3 seconds of running time. Partial points can be obtained if your program can solve only smaller test cases (for example, when the coordinates are between 0 and 100) within the allotted time.
The source code (s77.pas, s77.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s77.txt, s77.pdf, ...) - also describing which developer environment to use for compiling - should be submitted in a compressed file s77.zip.
Based on the idea of Gábor Gyebnár
(10 pont)
Deadline expired on February 11, 2013.
Sorry, the solution is available only in Hungarian. Google translation
Egy kisebb tesztesetekre működő egyszerű megoldási lehetőség, hogy a rácspontokat egy gráf csúcsainak fogjuk föl, és akkor kötünk össze éllel két csúcsot, ha szomszédosak, és akadály sem választja el őket egymástól. Ekkor egy szélességi bejárással meghatározhatunk egy legrövidebb utat.
Egy megoldást megkönnyítő észrevétel, hogy a robotnak érdemes minden olyan esetben az x tengely felé lépnie, amikor ezt megteheti. (Ez azért teljesül, mert bármikor léphet oldalra, hiszen nincsenek függőleges akadályok, vagyis nem fordulhat elő olyan, hogy valamilyen lehetőséget elveszít az x tengely felé lépéssel.) Emiatt elég, ha csak olyankor hagyunk döntési lehetőséget a robotunknak, amikor elér egy akadályt. Így akár átfogalmazhatjuk a feladatot robot helyett egy labdára, ami zuhan az x tengely felé, és ha ráesik egy "polcra", akkor eldöntheti, hogy a polc jobb vagy bal végéhez gurul el, mielőtt tovább zuhan.
Ezt figyelembe véve találhatunk egy, a fentebbihez képest lényegesen kisebb gráfreprezentációt a feladathoz: legyenek a gráfcsúcsok az akadályvégpontok, és minden u csúcsból vezessen él azon csúcsokba, amelyek megfelelnek annak az akadálynak a végpontjainak, amelyre ráesünk az u csúcsból. Az éleket súlyozzuk az áthaladás közben megtett távolsággal. Élsúlyozott gráfban legrövidebb út keresésére általános esetben a Bellman-Ford, vagy a Dijkstra algoritmust lehet használni, azonban észrevehetjük, hogy ebben a gráfban nincsen irányított kör, vagyis egy egyszerű dinamikus programozás is megteszi: y koordináta szerinti csökkenő sorrendben határozzuk meg a csúcsokra a hozzájuk vezető legrövidebb út hosszát, a következő rekurzív összefüggésből: D(u)=min{D(v)+W(v,u)|v-ből vezet út u-ba }.
A fentebbi gráfot könnyű O(n2) időben fölépíteni, azonban a legnagyobb tesztesetek megoldásához ez nem elég. O(nlog n) időben fölépíthetjük a gráfot egy "söprő egyenes" algoritmussal (ld. Topcoder tutorial). Képzeljük el, hogy egy függőleges egyenest végigtolunk a pályán mondjuk balról jobbra, és közben számon tartjuk, hogy mely akadályokat metszi. Amikor ez az egyenes elér egy u akadályvégpontot, akkor az egyenesen lévő következő (y koordináta szerint csökkenően) akadály lesz az, amelyikre u-ból esik. Ha az egyenest metsző akadályokat egy STL mapben tartjuk, akkor csak meg kell benne keresni az aktuális akadályt, és eggyel odébb kell léptetni az iterátort, ami O(log n) idejű művelet. Ez a megoldás implementálva: S77SweepLine.cpp
Egy másik lehetőség a gráf felépítésére, hogy lentről fölfelé dolgozzuk fel az akadályokat, és egy lazy propagation segment tree-ben tartjuk számon minden x-re a legmagasabb akadály indexét, vagyis hogy mely x koordinátákon mely akadályokra lehet éppen esni. Szilágyi Dániel megoldása ezt a módszert használja: S77SzilagyiDaniel.cpp
Egyébként pl. ebben az IOI feladatban a söprő egyenes módszert és a szegmens fát is be kell vetni: Pyramid Base
Statistics:
7 students sent a solution. 10 points: Szilágyi Dániel. 9 points: Jákli Aida Karolina, Juhász 326 Dániel. 8 points: 2 students. 5 points: 2 students.
Problems in Information Technology of KöMaL, January 2013
