A KöMaL 2019. novemberi fizika feladatai

M-jelű feladatok A beküldési határidő 2019. december 10-én LEJÁRT.

---

M. 390. Vízből készített prizmával, minél egyszerűbb módon bontsuk fel egy LED lámpa fehér fényét színeire! Írjuk le a módszert és az észlelés eredményét!

Közli: Tichy Géza, Budapest

(6 pont)

statisztika

G-jelű feladatok A beküldési határidő 2019. december 10-én LEJÁRT.

---

G. 685. Egy amerikai autó tankjába 15 gallon benzin fér. Hány mérföld utat tud megtenni a tulajdonos a teletankolt autóval, ha az autó európai katalógusa szerint a fogyasztása 6,5 liter/100 km?

(3 pont)

megoldás, statisztika

---

G. 686. Egy 1,5 tonna tömegű személyautó vízszintes úton áll. Mekkora felületen fekszik fel az autó az útra, ha a benzinkútnál beállított keréknyomás (túlnyomás) minden gumiabroncsban 2,5 bar?

(3 pont)

megoldás, statisztika

---

G. 687. Időjárásjelentésekben a hőmérséklet mellett a hőérzetet is fel szokták tüntetni, ami lehet alacsonyabb is, magasabb is, mint a hőmérővel mérhető adat. Ha a zuhanykabinban éppen befejezzük a zuhanyozást, akkor a fürdőszobában mérhetőnél magasabbnak érezzük a hőmérsékletet, ha viszont kinyitjuk a kabin ajtaját, mert kint hagytuk a törülközőnket, akkor a hőérzetünk azonnal sokkal alacsonyabb a fürdőszoba hőmérsékleténél. Magyarázzuk meg, mi az oka, hogy a hőérzetünk pillanatok alatt nagyot változik annak ellenére, hogy a fürdőszoba hőmérséklete közel állandó!

(3 pont)

megoldás, statisztika

---

G. 688. Régen a moziban a diavetítős mesefilmekhez hasonló filmszalagot használtak, csak az otthon vetítetteknél sokkal hosszabbakat. Egy percnyi film 27 méter hosszú szalagra fért rá. A filmszalagot tekercsekben tárolták, a tárolóorsó sugara 5,5 cm, erre 12,5 cm vastagon lehetett a filmet feltekercselni. Vetítés közben a film elhaladt a vetítőlencse előtt, majd egy másik, hasonló segédorsóra tekeredett fel.

$\displaystyle a)$ Mekkora fordulatszámmal forgott a tekercs a film lejátszásakor a vetítés elején és a végén?

$\displaystyle b)$ A vetítés után a segédorsóról visszatekercselték a filmet az eredeti orsóra. Mekkora fordulatszámmal forgott a segédorsó a tekercselés elején és a végén, ha az eredeti orsót végig 3 fordulat/másodperc fordulatszámmal forgatták?

(4 pont)

megoldás, statisztika

P-jelű feladatok A beküldési határidő 2019. december 10-én LEJÁRT.

---

P. 5164. Ugyanannyi idő alatt egy fonálinga 5, egy másik 10 kis amplitúdójú lengést végez. Milyen hosszúak az ingák, ha az egyik inga 120 cm-rel hosszabb a másiknál?

Példatári feladat nyomán

(3 pont)

megoldás, statisztika

---

P. 5165. Egységsugarú, homogén, kör alakú lemezből az ábrán látható módon kivágunk egymást kívülről érintő, rendre $\displaystyle \frac14, \frac18, \frac1{16}, \ldots$ sugarú, középpontjukkal az egyik sugárra illeszkedő köröket. Hol lesz a maradék idom tömegközéppontja, ha

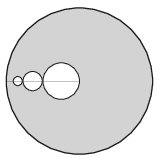
$\displaystyle a)$ csak a legnagyobb kört vágjuk ki;

$\displaystyle b)$ a két legnagyobb kört vágjuk ki;

$\displaystyle c)$ nagyon sok kört vágunk ki?

Közli: Tupi Zoltán, Budapest

(5 pont)

megoldás, statisztika

---

P. 5166. Egy Eötvös-inga $\displaystyle 2r=40$ cm-es rúdjának végeire egy-egy $\displaystyle m=30$ g tömegű, kicsiny testet erősítünk. A rendkívül könnyű rúd egy hajszálvékony fémszálon függ, vízszintes helyzetben. Közepétől mérve $\displaystyle R=3$ m távolságban, vele azonos magasságban egy $\displaystyle m^*=100$ kg tömegű ólomgolyót helyeztek el.

$\displaystyle a)$ Mekkora forgatónyomatékot gyakorol az ólomgolyó az ingára, amikor a golyót és az ingarúd közepét összekötő egyenes $\displaystyle \varphi$ szöget zár be a rúd irányával?

$\displaystyle b)$ Ábrázoljuk a forgatónyomatékot $\displaystyle \varphi$ függvényében! Mekkora szögnél lesz maximális a forgatónyomaték?

Közli: Cserti József, Budapest

(5 pont)

megoldás, statisztika

---

P. 5167. Egy mosogató csapját enyhén megnyitva beállíthatjuk, hogy a víz függőleges, folyamatos sugárban folyjék ki, és így érje el a mosogató vízszintes alját. Egyik alkalommal a vízsugár átmérője becsapódáskor háromnegyed akkora volt, mint 20 cm-rel magasabban.

$\displaystyle a)$ Mekkora volt ekkor a vízsugár becsapódási sebessége?

$\displaystyle b)$ Mekkora nyomást fejt ki a vízsugár a mosogató aljára?

Közli: Radnai Gyula, Budapest

(5 pont)

megoldás, statisztika

---

P. 5168. Egy $\displaystyle A$ alapterületű, $\displaystyle m$ tömegű dugattyúval elzárt hengerben $\displaystyle V_0$ térfogatú héliumgáz van. A dugattyút és a henger alját egy függőleges helyzetű, $\displaystyle D=400$ N/m rugóállandójú, kezdetben nyújtatlan rugó köti össze.

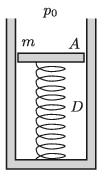
Mennyi hőt kell közölnünk a gázzal ahhoz, hogy a dugattyú $\displaystyle h$ magassággal megemelkedjen, ha a rendszer hőszigetelt?

Adatok: $\displaystyle A=7~\mathrm{dm}^2$, $\displaystyle m=5$ kg, $\displaystyle V_0=4~\mathrm{dm}^3$, $\displaystyle D=400$ N/m, $\displaystyle h=5$ cm és a külső légnyomás $\displaystyle p_0=100$ kPa.

Közli: Kis Tamás, Heves

(4 pont)

megoldás, statisztika

---

P. 5169. Az $\displaystyle L=20$ cm hosszúságú, homogén tömegeloszlású, $\displaystyle m=0{,}4$ kg tömegű rudat az egyik végénél a bal oldali ábra szerint az $\displaystyle A$ pontnál lévő csuklóhoz erősítjük, amely körül minden irányban foroghat. A rúd másik végét egy $\displaystyle D=25$ N/m direkciós erejű, függőleges helyzetű, erőmentes állapotban szintén $\displaystyle L$ hosszúságú rugóhoz rögzítjük. Kezdetben a rugó és a rúd egy egyenesbe esik. Ezt követően a rudat (a jobb oldali ábrán látható módon) $\displaystyle \varphi=60^\circ$-kal kitérítjük, majd elengedjük.

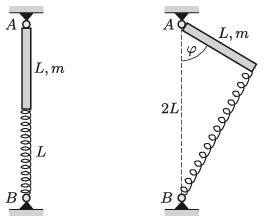
$\displaystyle a)$ Mekkora sebességgel lendül át a rúd vége a függőleges helyzeten?

$\displaystyle b)$ A rudat az egyensúlyi helyzetéből kis szöggel kitérítjük, majd elengedjük. Mennyi idő alatt jut a rúd függőleges helyzetbe?

$\displaystyle c)$ Mekkora szögsebességgel kell a rugó-rúd rendszert a függőleges $\displaystyle AB$ tengely körül forgatni, hogy a rúdnak a függőlegessel bezárt szöge folyamatosan $\displaystyle 60^\circ$ legyen?

(A súrlódás mindenhol elhanyagolható.)

Közli: Zsigri Ferenc, Budapest

(5 pont)

megoldás, statisztika

---

P. 5170. Dörzsöléssel feltöltött, egyforma szívószálak vízszintes síkban, egymással párhuzamosan úgy helyezkednek el, hogy a végeiket összekötő egyenesek merőlegesek a szívószálakra. Feltételezhetjük, hogy a töltések eloszlása a szálakon egyenletes, és mindegyik szívószálnak ugyanakkora a töltése. A két szélső szál rögzített, egymástól való távolságuk jóval kisebb, mint egy szívószál hossza. Közöttük még néhány olyan szívószál helyezkedik el, amelyek szabadon elmozdulhatnak. Hogyan helyezkednek el ezek a szabadon mozgó szálak, ha számuk

$\displaystyle a)$ kettő;

$\displaystyle b)$ három?

Közli: Márki-Zay János, Hódmezővásárhely

(5 pont)

megoldás, statisztika

---

P. 5171. Huzalból egyenlő oldalú háromszöget készítettünk, és két csúcsát az ábra szerint áramforráshoz kapcsoltuk. A hozzá vezető vezetékben 10 A erősségű áram folyik. Mekkora a mágneses indukció a háromszög középpontjában? (Az áramkör távol zárul.)

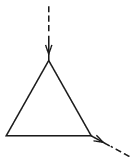
Közli: Holics László, Budapest

(4 pont)

megoldás, statisztika

---

P. 5172. Fényes evőkanalat tartunk 25 cm-re a szemünktől úgy, hogy a kanál szára függőleges. A kanál homorú felét nézve a fejünk fordított állású képét látjuk, míg a domború felét nézve a kép egyenes állású. Melyik képen látjuk a fejünk magasságát (függőleges méretét) nagyobbnak, és ez a kép hányszor nagyobb látószögben látszik a másiknál? A kanál függőleges metszetének görbületi sugara 5 cm.

Közli: Honyek Gyula, Veresegyház

(4 pont)

megoldás, statisztika

---

P. 5173. Egy $\displaystyle N=2000$ menetes, $\displaystyle L=5$ H induktivitású, elhanyagolható ohmos ellenállású körtekercs magja nagy mágneses permeabilitású gyűrű. A tekercs végeihez $\displaystyle R=200~\Omega$-os ellenállás csatlakozik. A tekercs egyik vége és ettől számított $\displaystyle N_1=300$-adik menete közé egy $\displaystyle U_0=1{,}5$ V feszültségű akkumulátor kapcsolható.

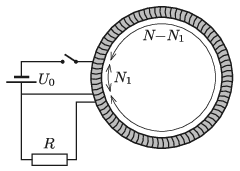
$\displaystyle a)$ Mekkora áram folyik a tekercs két részén $\displaystyle t_0=0{,}1$ s-mal a kapcsoló zárása után?

$\displaystyle b)$ Mekkora energiát ad le az áramforrás $\displaystyle t_0$ idő alatt, és mire fordítódik ez az energia?

A Kvant nyomán

(6 pont)

megoldás, statisztika

---

P. 5174. Egy illegális laboratórium ólomkonténerében olyan sugárzó anyagot találtak, amelyből másodpercenként $\displaystyle 2\cdot 10^{14}$ elektron lép ki. A rendőrségi jegyzőkönyvek szerint 53 évvel ezelőtt eltűnt 221 g cézium a közeli kutatóintézetből. Lehet-e a megtalált anyag az akkor eltűnt preparátum, ha azóta csak raktározták? (A cézium felezési ideje 26,6 év.)

Tematikus feladatgyűjtemény, Szeged

(4 pont)

megoldás, statisztika