A KöMaL 2020. januári matematika feladatai

K-jelű feladatok A beküldési határidő 2020. február 10-én LEJÁRT.

---

K. 644. Egy dobozban kék és zöld kockák vannak, összesen 70 darab. Kiveszünk négyszer annyi kék kockát, mint zöldet, így a dobozban maradt kockák között 7-szer annyi a zöld, mint a kék. Hány kék és hány zöld kocka volt a dobozban eredetileg?

(6 pont)

megoldás, statisztika

---

K. 645. Milyen maradékot kapunk, ha az $\displaystyle 1+4+7+\ldots+2020$ összeget 8-cal elosztjuk?

(6 pont)

megoldás, statisztika

---

K. 646. Van három gépünk, amelyek két-két bemenettel, és egy-egy kimenettel rendelkeznek. A gépek a bemeneteken keresztül megadott számokkal egy meghatározott műveletsort végeznek el, és ennek eredménye jelenik meg a kimeneten. A három gép tehát az ábra szerint néz ki.

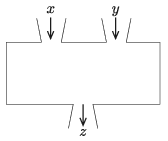
Az A gép kimenetén $\displaystyle x\cdot y$ jelenik meg, a B gép kimenetén $\displaystyle x^2+y$, a C gép kimenetén pedig $\displaystyle 5\cdot x+3\cdot y$ ($\displaystyle x$ és $\displaystyle y$ jelöli az egyik, illetve a másik bemeneten beadott számokat). Összekötjük az A, B és C gépeket olyan módon, hogy az egyik kiválasztott gép egy-egy bemenetére a másik két gép kimenetét kötjük rá. Mennyi lesz az utolsó gépből kijövő lehető legnagyobb eredmény, ha a két első gépbe egyaránt az $\displaystyle x=4$ és $\displaystyle y=7$ értékeket tápláljuk be?

(6 pont)

megoldás, statisztika

---

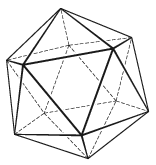
K. 647. Egy papírból készült ikozaédert néhány él mentén felvágunk úgy, hogy széthajtva a test valamelyik (síkban fekvő) hálójához jussunk. Hány élt kell felvágni ehhez?

(6 pont)

megoldás, statisztika

---

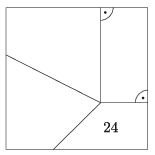
K. 648. Egy négyzet belső pontját összekötöttük minden oldalon az egyik oldalharmadoló ponttal az ábra szerint, és így négy négyszöget kaptunk. Ismerjük az egyik ilyen négyszög területét (lásd az ábrát). Határozzuk meg a többi négyszög területét.

(6 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2020. február 10-én LEJÁRT.

---

C. 1581. Adjuk meg $\displaystyle n$ azon pozitív egész értékeit, amelyekre $\displaystyle n!$ pontosan $\displaystyle 19\,531$ darab $\displaystyle 0$-ra végződik.

(5 pont)

megoldás, statisztika

---

C. 1582. Az $\displaystyle ABCD$ paralelogramma oldalaira kifelé az $\displaystyle ABP$, $\displaystyle BCQ$, $\displaystyle CDR$, $\displaystyle DAS$ szabályos háromszögeket rajzoltuk. Milyen feltételnek kell teljesülnie a paralelogrammára ahhoz, hogy $\displaystyle PQRS$ négyzet legyen?

(5 pont)

megoldás, statisztika

---

C. 1583. Ábrázoljuk a derékszögű koordinátarendszerben azokat a pontokat, melyeknek koordinátái kielégítik az alábbi egyenlőtlenséget:

$\displaystyle |x|+|y|+|x+y|\le 2.$

Mekkora területű síkidomot kaptunk?

(Horvát feladat)

(5 pont)

megoldás, statisztika

---

C. 1584. Legfeljebb mekkora területű négyzetet lehet legfeljebb három egyenes vágással kivágni egy háromszög alakú papírlapból, amelynek oldalai 3 cm, 4 cm és 5 cm hosszúak?

(5 pont)

megoldás, statisztika

---

C. 1585. Melyek azok a $\displaystyle p$ és $\displaystyle q$ egymástól különböző pozitív prímszámok, melyekre $\displaystyle p-4p^2+p^3=q-4q^2+q^3$?

(5 pont)

megoldás, statisztika

---

C. 1586. Az $\displaystyle ABC$ háromszög $\displaystyle AB$ oldalának harmadolópontjai $\displaystyle D$ és $\displaystyle E$. A $\displaystyle DE$ szakasz egy tetszőleges belső pontja $\displaystyle P$. Húzzunk párhuzamost a $\displaystyle PC$ egyenessel a $\displaystyle D$, illetve $\displaystyle E$ pontokon keresztül. Ezek az egyenesek az $\displaystyle AC$ és $\displaystyle BC$ oldalakat rendre a $\displaystyle Q$ és $\displaystyle R$ pontokban metszik.

Mutassuk meg, hogy a $\displaystyle PRCQ$ négyszög területe az $\displaystyle APQ$ háromszög területével egyenlő nagyságú.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1587. Oldjuk meg az

$\displaystyle \frac{x-1}{\sqrt x}-\frac{\sqrt x}{x-2}=\frac{\sqrt x}{2x-1}$

egyenletet a valós számok halmazán.

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2020. február 10-én LEJÁRT.

---

B. 5070. Egy szigeten kétféle ember él. Az igazmondók mindig igazat mondanak, a hazudósok mindig hazudnak. Tíz szigetlakó között kiosztottuk az $\displaystyle 1,2,\ldots,10$ számokat. Mindenki egy-egy különböző számot kapott. Ezután mindenkinek feltették a következő három kérdést: ,,A te számod páros?'', ,,A te számod osztható 4-gyel?'', ,,A te számod osztható 5-tel?''. Az első kérdésre hárman, a másodikra hatan, a harmadikra pedig ketten válaszoltak igennel. Mely számok vannak hazudósoknál?

Javasolta: Róka Sándor (Nyíregyháza)

(4 pont)

megoldás, statisztika

---

B. 5071. Legyen az $\displaystyle ABC$ háromszög $\displaystyle BC$ oldalának $\displaystyle B$-hez közelebbi harmadolópontja $\displaystyle A_1$, a $\displaystyle C$-hez közelebbi harmadolópontja $\displaystyle A_2$, a $\displaystyle CA$ oldal $\displaystyle C$-hez közelebbi harmadolópontja $\displaystyle B_1$, az $\displaystyle A$-hoz közelebbi harmadolópontja $\displaystyle B_2$, végül az $\displaystyle AB$ oldal $\displaystyle A$-hoz közelebbi harmadolópontja $\displaystyle C_1$, a $\displaystyle B$-hez közelebbi harmadolópontja $\displaystyle C_2$. Bizonyítsuk be, hogy az $\displaystyle A_1B_1C_1$ és $\displaystyle B_2C_2A_2$ háromszögek egybevágók és területük az $\displaystyle ABC$ háromszög területének harmadával egyenlő.

Javasolta: Bíró Bálint (Eger)

(3 pont)

megoldás, statisztika

---

B. 5072. Igazoljuk, hogy $\displaystyle \big[\sqrt n+\sqrt{n+3}\,\big]=\big[\sqrt{4n+5}\,\big]$ bármely pozitív egész $\displaystyle n$ esetén.

Javasolta: Imre Tamás (Marosvásárhely)

(3 pont)

megoldás, statisztika

---

B. 5073. Az $\displaystyle ABC$ háromszögbe írt körnek a háromszögoldalakkal párhuzamos érintői a háromszögből három kis háromszöget vágnak le, az ezekbe írt körök sugara 2, 3 és 10 egység. Mutassuk meg, hogy az $\displaystyle ABC$ háromszög derékszögű.

Javasolta: Róka Sándor (Nyíregyháza)

(4 pont)

megoldás, statisztika

---

B. 5074. Mely pozitív egész $\displaystyle n$-ekre és különböző (pozitív) $\displaystyle p$, $\displaystyle q$, $\displaystyle r$ prímszámokra teljesül, hogy

$\displaystyle \frac1{pq}+\frac1{pr^3}+\frac1{qr^2}=\frac1n ?$

Javasolta: Holló Gábor (Budapest)

(5 pont)

megoldás, statisztika

---

B. 5075. Az $\displaystyle ABCD$ konvex négyszög $\displaystyle AD$ és $\displaystyle BC$ oldalainak felezőpontja $\displaystyle E$, illetve $\displaystyle F$. Az $\displaystyle EF$ szakasz az $\displaystyle AC$ átlót a $\displaystyle P$ pontban, a $\displaystyle BD$ átlót $\displaystyle Q$-ban metszi. Bizonyítsuk be, hogy az $\displaystyle AEP$ és $\displaystyle BFQ$ körök az $\displaystyle AB$ egyenesen metszik egymást.

Javasolta: Holló Gábor (Budapest)

(5 pont)

megoldás, statisztika

---

B. 5076. Oldjuk meg az

$$\begin{align*} x+y+z+v & =0, \\ x^2+y^2+z^2+v^2 & = 12, \\ x^3+y^3+z^3+v^3 & = 24 \end{align*}$$

egyenletrendszert a valós számnégyesek halmazán.

(6 pont)

megoldás, statisztika

---

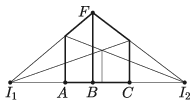
B. 5077. Egy kocka két iránypontos perspektív képét szeretnénk elkészíteni az ábra szerint. A két iránypont $\displaystyle I_1=(-9;0)$ és $\displaystyle I_2=(10;0)$; a kocka három csúcsának képe $\displaystyle A=(-3;0)$, $\displaystyle B=(0;0)$ és $\displaystyle C=(4;0)$. Mekkora legyen az $\displaystyle F$ pont $\displaystyle y$-koordinátája?

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2020. február 10-én LEJÁRT.

---

A. 767. Egy $\displaystyle n\times n$-es táblázat mezői mind különböző színűre vannak színezve. Egy lépés abból áll, hogy kiválasztunk egy sort, abban minden mezőt eggyel jobbra tolunk, a sor jobb szélső mezőjét pedig berakjuk a sor bal szélén lévő mező helyére; vagy kiválasztunk egy oszlopot, abban minden mezőt eggyel lefelé tolunk, és az oszlop legalsó mezőjét berakjuk az oszlop tetején lévő mező helyére. Milyen $\displaystyle n$ esetén lehet ilyen lépésekkel az $\displaystyle n^2$ darab mező összes lehetséges elrendezését megkapni?

Javasolta: Schweitzer Ádám

(7 pont)

statisztika

---

A. 768. Legyen $\displaystyle S$ egy olyan síkbeli alakzat, melyet néhány (véges sok) egységnégyzet uniójaként állítottunk elő. Bizonyítandó, hogy $\displaystyle S$ kerületének és területének az aránya legfeljebb 8.

(7 pont)

statisztika