A KöMaL 2020. májusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2020. június 10-én LEJÁRT. |
I. 511. Andi és Bandi a szorzás gyakorlására kitaláltak egy játékot. A játékban először választottak egy pozitív egész számot 1 és 1000 között. Ezután felváltva mondtak pozitív egész számokat, de csak olyat, amit korábban még nem mondott egyikük sem és nem nagyobb a választott számnál. A játék addig tartott, amíg valaki olyan számot nem mondott, amivel megszorozva bármelyik korábban elhangzott számot a szorzat a játék elején választott szám lett. Az veszített, aki az utolsó számot mondta.
Sokat játszottak, majd elkezdtek gondolkodni azon, hogy vajon mi lehet a kezdő vagy a másodiknak számot mondó játékos számára a nyerő stratégia. Rájöttek a módszerre, és arra is, hogy a választott számtól függ, hogy kinek kedvez a játék, de ezt nem nézték meg mind az 1000 esetre.
Találjuk ki, hogy mi lehet a nyerő stratégia, majd készítsünk programot, amely megadja, hogy adott választott szám esetén a kezdő vagy a második játékos tud-e nyerni, ha a stratégiát a játék során végig alkalmazza. A program bemenete a választott szám. A kimenetre írjunk 1-est, ha az első, és 2-est, ha a második játékosnak van nyerő stratégiája.
| Bemenet | Kimenet |
| 10 | 2 |
Beküldendő egy tömörített i511.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 512. A járványok az élővilág kialakulásával egyidősek. Az ilyen típusú populációbiológia rendszerek legtöbb átalakulása több egymás után következő lépésben megy végbe. Ezek a lépések tipikusan sorozatot alkotnak.
A járványterjedés modellezéséhez több-kevesebb paramétert vesznek figyelembe. Az egyik legegyszerűbb modellt, az SEIR-t vizsgáljuk meg táblázatkezelővel. Ebben a modellben a járványterjedés szempontjából négy csoportra osztjuk a populációt:
- \(\displaystyle S\) susceptible, azaz fogékonyak, még nem estek át a betegségen;
- \(\displaystyle E\) exposed, azaz lappangó, de még nem fertőző egyedek;
- \(\displaystyle I\) infectious, azaz fertőzöttek, betegek;
- \(\displaystyle R\) recovered, azaz gyógyultak.
Az osztályok közötti átalakulás: \(\displaystyle S \to E \to I \to R\).
Az emberek megfertőződnek és maguk is fertőzővé válnak, majd meggyógyulnak, vagy sajnos meghalnak. Az utóbbi tragédiával ez az egyszerű modell nem foglalkozik.
A betűk jelöljék, hogy hány egyed tartozik az egyes osztályokba. Vizsgáljuk meg, hogy az osztályok létszáma hogyan változik az időben néhány kezdeti paraméter mellett. Legyen a teljes populáció száma \(\displaystyle N\), így ekkor minden időpontban teljesül, hogy \(\displaystyle N=S+E+I+R\).
Egy új kórokozó esetén feltételezhetjük, hogy kezdetben a teljes populáció fogékony rá, azaz \(\displaystyle S\approx N\). Legyen
- \(\displaystyle \beta\) a kórokozó átadási valószínűsége egy fertőző és egy fogékony egyed között;
- \(\displaystyle \sigma\) a lappangók fertőzővé válásának sebessége;
- \(\displaystyle \gamma\) a betegek meggyógyulásának sebessége.
Ekkor a fogékony egyedek számának változása \(\displaystyle \Delta S=-\beta \cdot \frac{I}{N} \cdot S\), ahol az \(\displaystyle \frac{I}{N}\) hányados a fertőzöttek aránya a teljes populációhoz képest. Minél nagyobb ez az érték, annál gyorsabb a járvány terjedése.
A lappangó esetek száma éppen ennyivel növekszik, miközben egy részük beteggé válik:
\(\displaystyle \Delta E=\beta \cdot \frac{I}{N}\cdot S-\sigma \cdot E. \)
A fertőzöttek száma \(\displaystyle \sigma \cdot \)E-vel növekszik, és a meggyógyulókkal csökken:
\(\displaystyle \Delta I=\sigma \cdot E-\gamma \cdot I. \)
A gyógyultak számának változása
\(\displaystyle \Delta R=\gamma \cdot I. \)
Szimuláljuk a járvány kialakulását időegységenként (naponta). Minden lépésben számítsuk ki a jelenlegi adatok alapján a változásokat, majd a következő napon a megváltozott értékekkel dolgozzunk:
$$\begin{align*} S(n+1) & \leftarrow S(n)+\Delta S(n), &&& E(n+1)&\leftarrow E(n)+\Delta E(n),\\ I(n+1) & \leftarrow I(n)+\Delta I(n) & \text{és}&& R(n+1)&\leftarrow R(n)+\Delta R(n). \end{align*}$$A szimulációt legalább 150 napra végezzük el az alábbiak szerint:
- Az induló paramétereket a táblázat első néhány sorában lehessen megadni, helyüket feliratokkal jelezzük. Példaként \(\displaystyle N=10\,000\,000\); \(\displaystyle \beta =0{,}9\); \(\displaystyle \sigma =0{,}1\); \(\displaystyle {\gamma =0{,}2}\).
- Határozzuk meg a táblázat két cellájában, hogy hányadik nap lesz a fertőző betegek száma maximális és mekkora ez az érték.
- Ábrázoljuk az \(\displaystyle S\), \(\displaystyle E\), \(\displaystyle I\), \(\displaystyle R\) osztályok létszámát az idő függvényében. A diagram értelmezését feliratokkal segítsük.
Beküldendő egy tömörített i512.zip állományban a munkafüzet, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott táblázatkezelő neve és verziószáma.
(10 pont)
I. 513. (É). A sejtautomata elnevezés Neumann Jánostól származik az 1940-es évek elejéről, aki az önmagát reprodukáló gép logikáját, létrehozásának lehetőségeit vizsgálta. A leghíresebb sejtautomata a John Horton Conway által kitalált életjáték. Conway egy hónappal ezelőtt, 2020 áprilisában halt meg, így ezzel a feladattal rá is emlékezünk.
A Conway-féle életjátékban sejtek élnek egy kétdimenziós világban. A sejtek egy képzeletbeli táblázat egy-egy cellájában találhatók. Viselkedésüket az határozza meg, hogy az őket tartalmazó cella 8 szomszédja közül hányban található sejt. Ha egy sejt szomszédos cellái közül kettőnél kevesebb vagy háromnál több tartalmaz sejtet, akkor a sejt elpusztul, egyébként életben marad. Ha egy cella üres, de a szomszédos cellák közül pontosan háromban van sejt, akkor az üres cellában új sejt születik. A leírt változások nem folyamatosan, hanem lépésekben (generációkban) történnek. Kezdetben az élettér bizonyos celláiban vannak sejtek, míg a többi cellában nincsenek.
Például egy \(\displaystyle 6\times 6\)-os élettér hat egymást követő állapota (a szürke cellákban vannak sejtek, a sötétebbek új sejtek helyét mutatják):

Készítsünk programot sejtautomata néven egy \(\displaystyle 50\times 50\)-es négyzethálós életjátékhoz és oldjuk meg a következő feladatokat. A megoldások során a mintához hasonlóan valósítsuk meg a felhasználóval történő kommunikációt (az ékezetmentes kiírás is elfogadott).
1. Olvassuk be az élettér kezdeti állapotát a conway.txt szöveges állományból és tároljuk el az adatokat úgy, hogy a szimulációhoz használni tudjuk őket. A szöveges állomány 50 sorból áll, melyek mindegyikében 50 karakter található. Az állomány \(\displaystyle i\)-edik sorának \(\displaystyle k\)-adik karaktere az élettér \(\displaystyle i\)-edik sorának \(\displaystyle k\)-adik oszlopában lévő cella kezdeti tartalmát mutatja: szóköz esetén a cella üres, s betű esetén a cellában sejt van.
2. Adjuk meg, hogy összesen hány sejt található az élettérben.
3. Készítsünk függvényt szomszed néven, amelynek bemeneti paramétere \(\displaystyle i\) és \(\displaystyle k\), amelyek az élettér \(\displaystyle i\)-edik sorát és \(\displaystyle k\)-adik oszlopát jelentik. A függvény számítsa ki és adja vissza a megfelelő cella szomszédjaiban található sejtek számát. Kérjük be a felhasználótól egy oszlop és egy sor értékét, és adjuk meg, hogy az adott cellában van-e sejt, illetve azt, hogy a cella szomszédjaiban hány sejt található.
4. Készítsünk eljárást egylepes néven, amely elvégez egy szimulációs lépést. Vegyünk fel az eredeti élettér mellé még egy átmeneti tárolót, amely az élettér állapotát mutatja majd a következő generációban. Vizsgáljuk meg az élettér celláit a fenti leírásnak megfelelően, majd ez alapján adjunk értéket a most létrehozott átmeneti tárolónak. Az eljárás végén a kiszámított új élettér értékei kerüljenek a tárolóból az eredeti élettérbe.
5. Számítsuk ki, hogy hány olyan sejt van az élettérben, amely életben marad egy szimulációs lépés megtétele után, majd az eredményt jelenítsük meg.
6. Végezzük el a szimuláció \(\displaystyle n\) lépését az egylepes alprogram meghívásával, ahol \(\displaystyle n\) értékét a felhasználótól kérjük be.
7. Adjuk meg, hogy az eddig elvégzett \(\displaystyle n\) lépés után most hány sejt fog születni a következő szimulációs lépésben.
8. Adjunk statisztikát a szimuláció következő 100 lépésében az élettér állapotáról. Írjuk a statisztika.txt szöveges állomány egy-egy sorába az élettérben lévő sejtek, a következő szimulációs lépésben elpusztuló és születő sejtek számát egy-egy szóközzel elválasztva. Ha az élettér üres, tehát a sejtek kihalnak, akkor az állományba 0 0 0 tartalmú sorokat ne írjunk, hanem helyette a következő sor jelenjen meg: ,,A szimuláció 34. lépése után az élettér már nem tartalmaz sejteket.'' A szimulációs lépések közé a 6. feladatban végrehajtott \(\displaystyle n\) lépés is beleszámít.
Példa a be/kimenetre:

Letölthető állomány: conway.txt
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2020. június 10-én LEJÁRT. |
I/S. 45. Jenő az Alföld tengersík vidékéről felköltözött a Budai-hegyekbe. Hogy minél inkább otthon érezze magát, szeretné a kertjét átrendezni, hogy kevésbé legyen hegyes-völgyes. A kert \(\displaystyle N\) parcellából áll, az \(\displaystyle i\)-edik parcella tengerszint feletti magassága \(\displaystyle A_{i}\) méter. Jenőnek egy órába telik egy parcella tetejéről egy réteg 1 méter magasságú földet áthordani egy másik parcella tetejére (ekkor az egyik parcella magassága 1 méterrel csökken, a másiké 1 méterrel nő). Jenő akkor fogja magát otthonosan érezni, ha a kertben bármely két parcella magasságának eltérése nem nagyobb, mint \(\displaystyle K\) méter. Írjunk programot, amely megmondja, hogy minimum hány órát kell dolgoznia Jenőnek, hogy elégedett legyen a kertjével és otthonosan érezze magát új lakóhelyén.
Bemenet: az első sor tartalmazza a parcellák \(\displaystyle N\) számát és \(\displaystyle K\) értékét. A második sor \(\displaystyle N\) darab számot: az \(\displaystyle i\)-edik szám az \(\displaystyle i\)-edik parcella \(\displaystyle A_{i}\) tengerszint feletti magassága méterben.
Kimenet: egyetlen szám, amely megadja, hogy minimum hány órát kell dolgoznia Jenőnek, hogy bármely két parcella magasságának eltérése legfeljebb \(\displaystyle K\) legyen.
Példa:
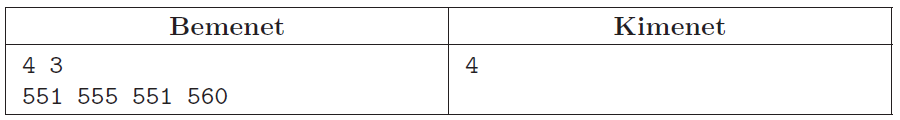
Korlátok: \(\displaystyle 1\le N,K,A_{i}\le 10^{5}\), egész számok. Időkorlát: 0,3 mp.
Értékelés: a pontok 50%-a kapható, ha \(\displaystyle N,K,A_{i}\le 1000\).
Beküldendő egy is45.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2020. június 10-én LEJÁRT. |
S. 144. Az asztalon \(\displaystyle N\) kockát találunk, az \(\displaystyle n\)-edik kocka élének hossza \(\displaystyle a_{n}\) egész szám, térfogata \(\displaystyle V_{n}\) (a kockákat 0-tól indexeljük). A kockákkal \(\displaystyle Q\) műveletet hajtunk végre egymás után. Az \(\displaystyle i\)-edik műveletben megváltoztatjuk az összes kocka élének hosszát az \(\displaystyle [l_{i},r_{i}]\) tartományban \(\displaystyle b_{i}\)-vel. Minden művelet után adjuk meg a kockák térfogatainak összegét modulo \(\displaystyle {10}^{9}\mathbf{+}7\).
Bemenet: az első sor tartalmazza az \(\displaystyle N\) és \(\displaystyle Q\) számot. A következő sor \(\displaystyle N\) pozitív számot tartalmaz: a kockák éleinek hosszát sorrendben, ezek legfeljebb \(\displaystyle {10}^{9}\) nagyságúak. A következő \(\displaystyle Q\) sor mindegyike tartalmaz egy \(\displaystyle l_{i}\), \(\displaystyle r_{i}\) és \(\displaystyle b_{i}\) egész számot (\(\displaystyle 0\le l_{i}\le r_{i}<N\), \(\displaystyle |b_{i}|\le {10}^{9}\)). A változtatások során a kockák éle mindig pozitív marad.
Kimenet: adjuk meg minden változtatás után a \(\displaystyle \bigg(\sum\limits_{n=0}^{N-1} V_{n}\bigg)\) modulo \(\displaystyle 10^{9}+7\) értéket.
Példa:
| Bemenet (a / jel sörtérést helyettesít) | Kiment |
| 5 2 1 1 1 1 2 0 1 1 / 4 4 -1 | 26 19 |
Korlátok: \(\displaystyle 1\le N, Q\le {10}^{5}\). Időkorlát: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha \(\displaystyle N, Q\le 100\).
Beküldendő egy s144.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.
