A KöMaL 2022. szeptemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2022. október 17-én LEJÁRT. |
I. 568. Az öreg király összehívta tanácskozásra férfi leszármazottjait. Így eljöttek a fiai, unokái, dédunokái stb. A király memóriája már nem a legjobb, és a tanácskozás elején szeretné tudni mindenkiről, hogy hány generációs távolságban van tőle. Készítsünk programot, amely az \(\displaystyle N\) tagú család minden jelenlévőjéről megadja, hogy hány generációra van a királytól az írnok feljegyzései alapján.
A standard bemenet (az írnok adatai) első sorában a jelenlévők \(\displaystyle N\) (\(\displaystyle 2\le N\le 50\)) száma van. Az ezt követő \(\displaystyle N-1\) sor mindegyike egy számpárt tartalmaz: az \(\displaystyle A\) apa és \(\displaystyle F\) fia (\(\displaystyle 1\le A, F\le N\)) sorszámát szóközzel elválasztva.
A standard kimenetre két sort írjunk ki: az elsőbe a király sorszámát, a másodikba pedig emelkedő sorszám szerint mindenkinek a generációs távolságát a királytól.
| Példa bemenet | Kimenet |
|---|---|
9 3 1 3 2 7 3 5 6 4 5 7 4 8 9 7 8 | 7 2 2 1 1 2 3 0 1 2 |
Beküldendő egy tömörített i568.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 569. Az egyik nap Piroska néni, a matektanár egy dobozzal a kezében lépett be a 9.a osztálytermébe. A tanóra elején megszokott események után felnyitotta a korábban a tanári asztalra letett dobozt.
– Nézzétek csak, micsoda csodás valamit hoztam! – emelt ki a dobozból egy dodekaédert. – Ez az öt szabályos test egyike, 12 darab szabályos ötszöglapja van, dodekaédernek hívják. Ha a lapokra felírjuk a számokat 1-től 12-ig, akkor a dobókocka kétszeresét készíthetjük el. Mivel harmincan vagytok, hoztam is 60 dobókockát és 30 dobódodekaédert. Andris, ha elmondtam a feladatot, segíts kiosztani, légy szíves. Mindhárom testtel maximum 100 alkalommal kell dobnotok. A füzetbe jegyezzétek fel minden dobásnál a kockákkal dobott számok összegét, mellé a dodekaéderrel dobott értéket! A két kockával és a dodekaéderrel dobást csak addig kell ismételgetni, amíg a két kockán kapott összeg, vagy a dodekaéderen kijött érték 12 nem lesz. Aztán már csak a másik fajta dobást kell tovább ismételnetek, amíg az is 12 nem lesz, de ne felejtsétek, csak 100 kísérletet végezhettek. Végül csak két adatra lesz szükségünk, a dobódodekaéderrel és a dobókockapárral végzett kísérletek számára. Remélem, minden világos, Andris, gyere, segíts az eszközöket kiosztani. Közben lehet tippelni arra, hogy mekkora lesz a dobásszámok átlagának aránya.
– Nyilván azonos lesz nagyjából, hisz a dodekaéder pont olyan, mint a két dobókocka – kiabált be Miki. Sokan helyeslően bólogattak.
– No, majd kiderül – válaszolta Piroska néni. – Kezdjétek a kísérleteket!
Segítsünk a 9.a osztálynak!
1. Hozzuk létre a dodekaéder munkafüzetet a táblázatkezelő alapértelmezett fájlformátumában.
2. Készítsük fel a munkalapot a 30 tanuló legfeljebb 100 kísérletének dokumentálására:

3. A C1:CX1 tartományt töltsük fel az \(\displaystyle \mathtt{1, 2, \ldots, 99, 100}\) értékekkel. Az A2:A61 tartományt pedig egyetlen, másolható függvény segítségével az \(\displaystyle \mathtt{1, 1, 2, 2, \ldots, 29, 29, 30, 30}\) értékekkel. A B2:B61 tartományt felváltva a ,,két dobókocka'' és a ,,dobódodekaéder'' szövegekkel töltsük fel. Végül készítsük el az A1:CX1 tartomány szegélyezését a minta szerint.
4. Ezek után modellezzük a kísérletet.
\(\displaystyle a\). A C2 cellába kerüljön a véletlenszám-generátort használó olyan függvény, amely a két független kockadobás összegének értékét jeleníti meg a cellában.
\(\displaystyle b\). A C3 cellába kerüljön hasonló függvény, amely a dobódodekaéderrel végzett dobás értékét jeleníti meg a cellában.
\(\displaystyle c\). A C2:C3 tartomány képleteit másoljuk le a C4:C61 tartományra.
\(\displaystyle d\). A D2 cellába kerüljön a C2 celláéhoz hasonló függvény, de, ha a C2 cella értéke 12, akkor a D2 cella legyen üres. Járjunk el hasonlóan a \(\displaystyle \mathtt{D3, C3}\) cellapárral.
\(\displaystyle e\). A D2:D3 tartomány képleteit másoljuk le a D4:D61 tartományra.
\(\displaystyle f\). Az E2 cellába kerüljön a D2 celláéhoz hasonló függvény, de, ha a D2 cella értéke üres vagy 12, akkor az E2 cella legyen üres. Járjunk el hasonlóan az \(\displaystyle \mathtt{E3, D3}\) cellapárral.
\(\displaystyle g\). A D2:D3 tartomány képleteit másoljuk le a D2:CX61 tartományra.
5. A CY2:CY61 tartomány celláiba kerüljön olyan függvény, amely megadja az adott sor dobásainak számát a 12-es érték eléréséig.
6. A C62 és a C63 cellákba kerüljön a dobókockával, illetve dobódodekaéderrel tanulónként végzett dobások átlaga egészre kerekítve.
7. Vizsgáljuk meg a kapott értékpárt, és írjunk a tapasztaltakról magyarázatot a dokumentációba.
A megoldásban saját függvény vagy makró nem használható!
Beküldendő egy tömörített i569.zip állományban a táblázatkezelő munkafüzet (dobódodekaéder.xlsx, dobódodekaéder.ods, ...), illetve egy rövid dokumentáció (dobódodekaéder.txt, dobódodekaéder.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma és a válasz a 7. feladatra.
(10 pont)
I. 570. (É.) Tavaly ősszel Paolo Panzani megházasodott, elvette magyar barátnőjét, Budapesten folytatják életüket. Paolo pizzasütő mester, így 2022 áprilisában beindult a Pizza Panzani – online pizzaműhely. A finom pizzák híre gyorsan terjedt a neten, nyárra már közel ezer vásárló regisztrált oldalukon. Rendelést leadni 10 órától este 22 óráig lehet. A belvárosban álló műhelyükből kizárólag a belső kerületekbe szállítanak a műhely saját futárával. A rendelési rendszert úgy alkották meg, hogy amennyiben egy rendeléskor többféle (akár méret, akár fajta szerint) pizzát is rendelnek, azokat a rendszer külön rendelésként kezeli, a megrendelő azonosítója és a dátum árulkodik a többféle tétel rendelésről.
Erika, Paolo felesége a júliusi rendelések alapján szeretné a vállalkozást továbbfejleszteni akciók bevezetésével (akciós ár; egyet fizet, kettőt kap; boldog óra; a hónap minden negyedik rendelése féláron). Az informatikában jártas bátyja, Alex egy adatbázist készített, a következő táblákkal:
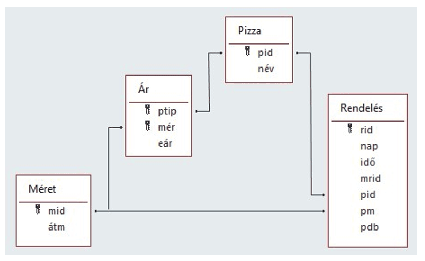
Pizza (pid, név)
pid a pizzafajta azonosítója (számláló) ez a kulcs;
név a pizzafajta megnevezése.
Méret (mid, átm)
mid a méret azonosítója (számláló) ez a kulcs;
átm a pizza átmérője cm-ben (szám).
Ár (ptip, mér, ár)
ptip a pizzafajta azonosítója (szám) ez az összetett kulcs része;
mér a pizza méretének azonosítója (szám) ez az összetett kulcs része;
eár a pizza egységára Ft-ban (szám).
Rendelés (rid, nap, idő, mrid, pit, pm, pdb)
rid a rendelés azonosítója (számláló) ez a kulcs;
nap a hónap napja (szám);
idő a rendelés napon belüli ideje [10:00–22:00] (idő);
mrid a rendelést leadó azonosítója (szám);
pit a pizzafajta azonosítója (szám);
pm a pizza méretének azonosítója (szám);
pdb a rendelt darabszám (szám).
Hozzuk létre adatbázist panzani néven! Importáljuk az adatbázisba a szövegfájlok nevével megegyező táblákba a pizza.txt, a méret.txt, az ár.txt és a rendelés.txt szövegfájlok tartalmát! A fájlok UTF-8 kódolásúak, tabulátorral tagoltak, első sorukban a mezőnevek szerepelnek.
A táblák kapcsolatát a következő ábra mutatja:
A következő kérdések megválaszolásakor és feladatok megoldásánál a lekérdezéseket és a jelentést a zárójelben olvasható néven mentsük. Ügyeljünk arra, hogy a megoldásban pontosan a kívánt mezők szerepeljenek. Gondoskodjunk arról, hogy a lekérdezések értelmes mezőnevei a mező tartalmára utaljanak és hogy az adatok értékei mindenhol teljes szélességükben legyenek olvashatók.
1. Jelenítsük meg a 24 cm-es pizzák nevét és egységárát növekvő egységár, azon beül a pizza neve szerint alfabetikus rend szerint. (1árak24)
2. Melyik a hat legnépszerűbb pizza, azaz amelyekből a legtöbbet rendeltek? A pizza nevét és a rendelt darabszámot szeretnénk látni. (2nyero)
3. Kik azok a visszatérő vásárlók, akik több, mint három napon is rendeltek a hónapban? (3tobb_szor)
4. Melyik napon kapták a legtöbb darabra a megrendelést? Feltehetjük, hogy egy ilyen nap volt. (4maxdb)
5. Melyik pizzákból hányszor rendeltek egyszerre több darabot? (5tobbdb)
6. Átlagosan melyik órában érkezett a hónapban a legtöbb rendelés? (6ora)
7. Mekkora volt a bevétel az egyes pizzafajtákból? A lekérdezés sorai bevétel szerint csökkenő sorrendben legyenek rendezettek. (7bevetel)
8. Melyik méretű pizzából mennyi fogyott a hónap során? (8meret)
9. Készítsük jelentést, amely megadja, hogy aznap, amikor a legtöbb rendelést kapták, melyik pizzából mennyit rendeltek az egyes méretekből. A jelentés az alábbi minta elrendezését kövesse. (9legjobbnap)

Beküldendő egy tömörített i570.zip állományban a panzani adatbázis, vagy az adatbázis tábláit létrehozó, valamint a feladatok megoldását adó SQL-parancsok egy szöveges állományban, és egy rövid dokumentáció, amely tartalmazza az alkalmazott adatbázis-kezelő program nevét és verziószámát.
Letölthető állományok egy tömörített mappában: panzani-forras.zip
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2022. október 17-én LEJÁRT. |
I/S. 64. Budapest belvárosában innovatív futárcéget alapítottak. A belvárost a cég egy \(\displaystyle N\) sorból és \(\displaystyle M\) oszlopból álló négyzetrácsként képzeli el. A négyzetrács \(\displaystyle n\)-edik sorában és \(\displaystyle m\)-edik oszlopában található egységnégyzetet \(\displaystyle T[n][m]\)-el jelöljük. A cég székhelye a \(\displaystyle T[a][b]\) mezőn helyezkedik el. A sorokat és oszlopokat 1-től indexeljük.
Egy nap rendelést kapnak a \(\displaystyle T[p][q]\) mezőről, ahova a futár szeretne a lehető leggyorsabban eljutni. Sajnos a futár még csak pályakezdő, ezért csak a sakkjáték futóra vonatkozó szabályai szerint tud mozogni Budapest belvárosában (csak átlósan mozoghat, de egy irányban tetszőlegesen sokat, ha a belvárosban marad).
Adjuk meg, hogy legkevesebb hány lépés alatt juthat el a futár a \(\displaystyle T[a][b]\) mezőről a \(\displaystyle T[p][q]\) mezőig, ha egy lépésben átlósan léphet tetszőlegesen sokat (a belvárosban maradva). Ha a futár sehogy sem tudja elérni a \(\displaystyle T[a][b]\) mezőt, akkor írjunk ki \(\displaystyle -1\)-et.
A bemenet első sorában az \(\displaystyle N\) és \(\displaystyle M\) számok szerepelnek szóközzel elválasztva. A második sorban az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle p\), \(\displaystyle q\) számok szerepelnek szóközzel elválasztva.
A kimenet egyetlen sorában egy szám szerepeljen, a minimális lépésszám (vagy \(\displaystyle - 1\), ha nem lehetséges elérni a célmezőt).
Példák:
| Példa bemenet | Kimenet |
|---|---|
5 4 2 2 4 4 | 1 |
12 4 1 1 11 3 | 4 |
Beküldendő egy tömörített s64.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Korlátok: \(\displaystyle 2 \le N,M \le 10^{9}\), \(\displaystyle 1 \le a, p \le N\), \(\displaystyle 1 \le b,q \le M\). Időkorlát: 0,4 mp.
Értékelés: a pontok 50%-a kapható, ha a program az \(\displaystyle N,M \le 1000\) tesztesetekre helyes megoldást ad.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2022. október 17-én LEJÁRT. |
S. 163. Manapság több olyan sakkmotor (sakkozó robot) létezik, mely képes a legjobb sakknagymestereket is legyőzni. A probléma nehézségét szeretnénk illusztrálni ezzel a feladattal, melyben jelentősen könnyítünk a feltételeken.
Adott egy hagyományos sakktábla, melyen egy világos gyalog és a két király található. Az esetek nagyjából 2/3-ában világos mattot tud adni a sötét királynak, a figurák elhelyezkedésétől függően azonban a kimenetel döntetlen is lehet (sötét nem nyerhet). Készítsünk számítógépes programot, amely megadja, hogy mi lesz a játék kimenetele egy ilyen állás esetén.
Bemenet: a bemenet első és egyetlen sora egy sakkállást tartalmaz a Forsyth–Edwards jelölés (FEN) szerint. Ez egy standard sakkállások jelölésére. Figyelem! A standard azt is megadja, hogy melyik játékosnak kell lépni. Ez befolyásolhatja a kimenetet. Feltételezhetjük, hogy az 50 lépés számlálója nulláról indul, így a lépésszám miatt nem lesz döntetlen az eredmény, ha világos nyerni tud.
Kimenet: a kimenet első és egyetlen sorába a W karaktert kell írni, ha világos nyerhet, és a B karaktert, ha sötét kikényszerítheti a döntetlent (mindkét fél optimálisan játszik).
Példa:
| Bemenet | Kimenet |
|---|---|
7k/4PK2/8/8/8/8/8/8 b - - 0 0 | W |
Magyarázat: ebben az állásban sötét lép, majd fehér három lépésben mattot ad.
Időkorlát: 1 mp.
Értékelés: A pontok 50%-a kapható, ha a program helyes eredményt ad olyan bemenetre, amikor a gyalog a 7. sorban van.
Segítség: játékállásokat kipróbálhatunk és tesztelhetünk például a https://www.chess.com/analysis és a https://syzygy-tables.info/ oldalakon.
Beküldendő egy s163.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

