A KöMaL 2022. novemberi informatika feladatai

I-jelű feladatok A beküldési határidő 2022. december 15-én LEJÁRT.

I. 574. Egy hosszú polcon dobozok helyezkednek el sorban egymás mellett, melyeket pozitív egész számok azonosítanak. Egy robot képes arra, hogy a polcról levegyen egy dobozt, képes arra, hogy magánál tartson egy dobozt, és képes arra, hogy a polcon egy üres helyre elhelyezze a magánál tartott dobozt. Ezenkívül a robot a polc elejétől a végéig tud mozogni előre és vissza, akár úgy is, hogy dobozt hoz magával, valamint képes arra, hogy mozgás közben egy polcon lévő dobozt egy szomszédos üres helyre toljon át. A robot rendező algoritmusa a következők szerint vezérli a robotot:

1. Elindul a polc elejétől, és ha van olyan doboz, amely nagyobb azonosító számmal rendelkezik, mint az utána következő doboz, akkor azt leveszi a polcról.

2. Mozog tovább a polc vége felé, miközben tartja a kivett dobozt, és minden olyan dobozt a polc eleje felé tol a szomszédos üres helyre, amely kisebb azonosító számú, mint az a doboz, amit a kezében tart.

3. Ha talál olyan dobozt, amely nagyobb azonosító számú, mint a kezében tartott doboz, akkor azt már nem tolja a polc eleje felé, hanem az azt megelőző üres helyre leteszi a magánál tartott dobozt. Ezután visszatér a polc elejére, ahol az 1. pont szerint kezdi ismét a működését.

4. Ha a polc elejétől indulva nem talál olyan dobozt, amely nagyobb azonosító számmal rendelkezne, mint a következő doboz, akkor abbahagyja a rendezést, mivel a dobozok az azonosító számok szerint növekvő sorrendben vannak.

Készítsünk programot, amely adott dobozok esetén megadja, hogy a robotnak hányszor kell levennie dobozt a polcról, illetve hányszor kell egy hellyel odébb tolnia dobozt!

A program a standard bemenet első sorából olvassa be a dobozok \(\displaystyle N\) számát (\(\displaystyle 2\le N\le 20\)), majd a második sorából a dobozok azonosító számát, \(\displaystyle N\) darab különböző pozitív egészet. A program a standard kimenet egyetlen sorába írja ki, hogy hányszor kellett a robotnak a rendezés során levennie egy dobozt, illetve hányszor kellett egy szomszédos helyre odébb tolnia egy dobozt.

Példák:

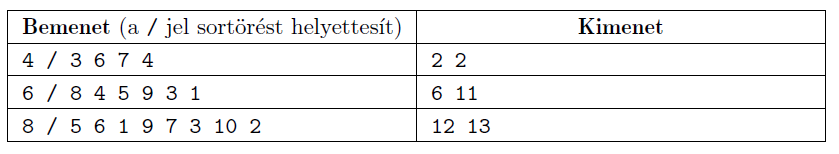
Beküldendő egy tömörített i574.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

I. 575. Egy kiszámolóban tíz ember áll körben, és a következő szabályok szerint játszanak:

1. Először mindenki gondol egy négyjegyű egész számra. Ezután a játék menetekből áll addig, amíg valakinek 0 nem lesz a száma. Ekkor ő a kiszámoló nyertese.

2. Az első menet előtt véletlenszerűen kisorsolnak egy játékost a 10-ből, ő lesz az első menetben a ,,számoló''.

3. A ,,számoló'' megnézi a számának utolsó számjegyét (legyen ez \(\displaystyle k\)), és számol saját magától indulva k lépést a körben előre, így kiszámolja a következő körben ,,számoló'' játékost. Ha \(\displaystyle k\) értéke 0, akkor ismét ő lesz a számoló. Ezután elhagyja a saját számának utolsó jegyét, és az így kapott szám az ő száma.



4. A játék minden menetében a 3. pontban leírtak szerint jár el a számláló, kivéve akkor, ha az ő száma már egyjegyű. Ebben az esetben a játék véget ér, ő a nyertes.

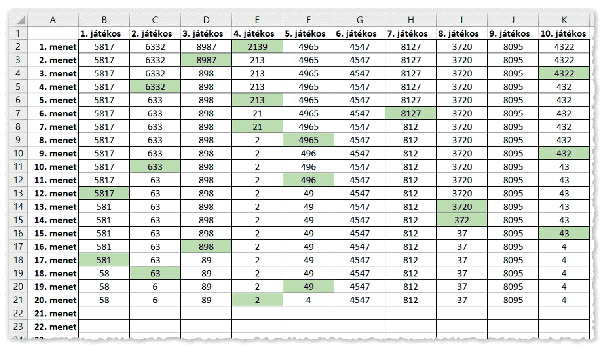
Szimuláljuk a játékot táblázatkezelő segítségével az alábbi mintát felhasználva. Minden sorban számítsuk ki az egyes játékosok számát, illetve jelezzük feltételes formázással, hogy ki a számoló játékos. A táblázatban csak az utolsó menetig jelenjenek meg adatok, de a munkafüzet legyen felkészítve a lehető leghosszabb, azaz legtöbb menetből álló játékra is.

A megoldást a táblázatkezelő beépített függvényeivel készítsünk el, az L oszloptól jobbra segédcellákat használhatunk, de saját függvényt vagy makrót ne alkalmazzunk. A táblázat formázását a mintához hasonlóan alakítsuk ki.

Beküldendő egy tömörített i575.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.

(10 pont)

megoldás, statisztika

I. 576. (É). A digitális kultúra emelt szintű érettségi vizsga gyakorlati feladatsorában az adatbázis-kezelési feladatot az XAMPP nyílt forráskódú webszerver és adatbázis-kezelő rendszerrel kell megoldani. A vizsgázó SQL-parancsok formájában kapja meg az adatbázist, a táblákat létrehozó és adatfeltöltő eljárásokat. Ebben a feladatban az érettségihez hasonló feladatokat kell megoldani, illetve az adatbázis létrehozását is nekünk kell elvégezni.

A Nemzet Művésze díj a legmagasabb művészi elismerés, amelyet 2014 óta osztanak ki. A jelenlegi és a már elhunyt díjazottakról a magyar nyelvű Wikipédia oldalán adatok állnak rendelkezésre, amit forrásként használhatunk:
https://hu.wikipedia.org/wiki/A_Nemzet_Művésze.

Az itt található adatok segítségével hozzuk létre azt a nemzetmuvesze.sql állományt, amelyet végrehajtva létrejön az adatbázis, a szükséges táblák a megfelelő számú, típusú, beállítású mezőkkel és az adatok feltöltése is megtörténik a táblákba. Ügyeljünk arra, hogy kiszámítható, felesleges adatokat ne tároljunk.

A következő feladatok megoldó SQL parancsokat rögzítsük a feladatok végén zárójelben megadott nevű és .sql kiterjesztésű szöveges állományokban. A lekérdezésekben pontosan a kívánt mezők szerepeljenek, felesleges mezőt ne jelenítsünk meg.

1. Mentsük le a megadott webcímről a Nemzet Művésze-díj adatait.

Tetszőleges alkalmazással rendezzük át, töröljük ki a felesleges, illetve egészítsük ki a szükséges adatokkal a táblákat. Használhatunk például szövegszerkesztőt, táblázatkezelőt vagy készíthetünk saját programot is. Az átalakítás egyes lépéseit más-más programmal is végezhetjük. A rendezett adatokat utolsó lépésként TXT típusú, tabulátorokkal tagolt UTF-8 kódolású egyszerű szöveges állományokként mentsük, amelyek neve a táblanevekkel egyezzen meg. Az állományok első sora tartalmazza a mezőneveket az azonosításhoz.

2. Készítsünk új adatbázist nemzetmuvesze néven. Készítsük el az adattáblákat az adatbázisban. A létrehozás során állítsuk be a megfelelő típusokat és elsődleges kulcsokat! (2nemzet)

3. Töltsük be az adattáblákba az adatokat a szöveges állományokból!

4. Lekérdezés segítségével írassuk ki, hogy Rubik Ernő milyen művészeti ágban és hány évesen nyerte el a címet. (4rubik)

5. Készítsünk lekérdezést, amely meghatározza, hogy melyik évben adták ki utoljára a Nemzet Művésze díjat. (5utolso)

6. Lekérdezés segítségével adjuk meg, hogy ki a legfiatalabb díjazott és mennyi idős a lekérdezés futtatásának pillanatában. (6fiatal)

7. Lekérdezés segítségével adjuk meg, hogy a jelenlegi díjazottak közül hányan tartoznak az egyes művészeti ágakhoz. A létszám mellett a művészeti ágak nevei jelenjenek meg. (7stat)

8. Soroljuk fel lekérdezés segítségével Varga Imrével együtt azoknak a nevét, akik vele azonos évben kapták meg a kitüntetést. (8varga)

9. Listázzuk ki azon díjazottak nevét és művészeti ágát, akiknek a művészeti tevékenysége ebben a körben ritka, azaz kevesebb, mint 5 személynél szerepel az adatbázisban. (9ritka)

Beküldendő egy tömörített i576.zip állományban az adatbázist létrehozó szöveges állomány és a feladatok megoldását adó lekérdezések.

(10 pont)

statisztika

I/S-jelű feladatok A beküldési határidő 2022. december 15-én LEJÁRT.

I/S. 66. Bábel tornyát több évszázada folyamatosan építik, és (a földszinten kívül) már \(\displaystyle N\) emelettel rendelkezik. Hillalum (egy kőműves, akit most vettek fel, hogy segítsen az építkezésen) a földszinten áll és felkészül az akár több hétig tartó lépcsőzésre, mire feljut a torony legfelső emeletére.

Mivel a torony minden emeletén más-más turisztikai látványosság kapott helyet, Hillalum tudja, hogy egy nap csak \(\displaystyle D\) emeletet fog feljebb mászni. Sőt, minden \(\displaystyle T\)-edik nap pihenőt tart, és egyáltalán nem lépcsőzik aznap. Hillalum csak nappal mászik felfelé, éjszaka azonban a kőművesek mindig hozzáépítenek még \(\displaystyle X\) darab emeletet a toronyhoz.

Adjuk meg, hogy Hillalumnak hány napba telik, mire feljut a torony legfelső emeletére.

A bemenet egyetlen sorában az \(\displaystyle N\), \(\displaystyle D\), \(\displaystyle T\) és \(\displaystyle X\) számok szerepelnek szóközzel elválasztva.

A kimenet egyetlen sorában egy szám szerepeljen, hogy hány nap alatt jut fel Hillalum a torony tetejére (vagy -1, ha sosem ér fel a legfelső emeletre).

Példák:

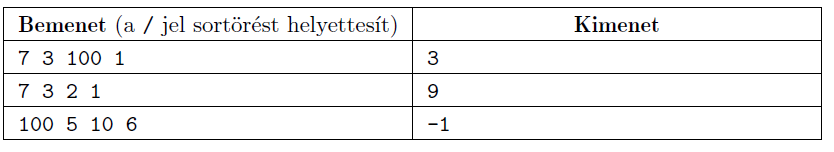
Korlátok: \(\displaystyle N,D,T, X \le 10^{9}\); \(\displaystyle 0 \le X\); \(\displaystyle 1 \le N,D\); \(\displaystyle 2 \le T\). Időlimit: 0,4 mp.

Értékelés: a pontok 50%-a kapható, ha a program helyes kimenetet ad \(\displaystyle N,D,T,X \le 100\) esetén.

Beküldendő egy is66.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2022. december 15-én LEJÁRT.

S. 165. Egy gyorsétteremlánc két különböző étteremben dolgozó alkalmazottja rájött, hogy ha a jelenlegi munkahelyük helyett egymás munkahelyére járnának dolgozni, akkor mindkettőjüknek kevesebbet kellene utazni. Szeretnének javaslatot tenni a felettesüknek a munkahelyek újraosztására, de a probléma sajnos túl bonyolultnak bizonyult, hogy papíron kiszámolják.

Adott egy város úthálózata, mely csúcsokból és az őket összekötő súlyozott élekből áll. Van továbbá valahány éttermünk és \(\displaystyle D\) alkalmazottunk, akikről tudjuk, honnan és hova járnak dolgozni. A feladatunk úgy újraosztani a munkahelyeket, hogy az alkalmazottak munkahelytől vett távolságának összege a lehető legkisebb legyen. (Tegyük fel, hogy a dolgozóknak egyéb preferenciája nincs.)

A bemenet első sorában a csúcsok \(\displaystyle N\) és az élek \(\displaystyle M\) száma található. A következő \(\displaystyle M\) sor egy-egy utat ír le, a két végpontjának sorszámával és az él súlyával (az út hosszával). Ezután az alkalmazottak \(\displaystyle D\) száma, majd \(\displaystyle D\) sorban az alkalmazottak lakhelyének és munkahelyének csúcsszáma található. Mindent 0-tól indexelünk és egy csúcsban legfeljebb egy étterem van.

A kimenet egyetlen sorában az elérhető legkisebb távolságösszeg szerepeljen, ha az újraosztás után minden étteremben ugyanannyian dolgoznak, mint előtte.

Példa:

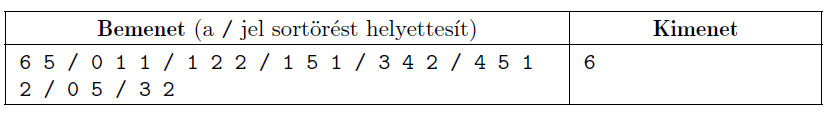
Megjegyzés: Mint ahogy a példa is mutatja, előfordulhat, hogy valaki így többet fog utazni.

Korlátok: \(\displaystyle N \le 500\), \(\displaystyle M \le 1000\), \(\displaystyle D \le 100\). Időlimit: 1 mp.

Értékelés: A pontok 50%-a kapható, ha a program helyes kimenetet ad a \(\displaystyle {D \le 10}\) esetekre.

Beküldendő egy s165.zip tömörített állományban a megfelelően dokumentált és kommentezett forrásprogram, amely tartalmazza a megoldás lépéseit, valamint megadja, hogy a program melyik fejlesztői környezetben futtatható. A dokumentáció tartalmazza a megoldás elméleti hátterét, az esetleg felhasznált forrásokat. Ne tartalmazzon kódrészleteket, azok magyarázata kódkommentek formájában a forrásprogramban szerepeljen.

(10 pont)

statisztika