A KöMaL 2024. januári matematika feladatai

K-jelű feladatok A beküldési határidő 2024. február 12-én LEJÁRT.

---

K. 794. \(\displaystyle 10\,000\) €-t befektettünk egy évre, ebből \(\displaystyle 4000\) €-t évi \(\displaystyle 5\%\)-os, \(\displaystyle 3500\) €-t évi \(\displaystyle 4\%\)-os kamatra. Hány százalékos kamatot kapunk a maradék összegre, ha a befektetésünk összesen \(\displaystyle 500\) € hasznot hoz?

(5 pont)

megoldás, statisztika

---

K. 795. Négy különböző pozitív prímszám szorzata \(\displaystyle n\). Hányféle különböző, \(\displaystyle n\) db kiskockából álló téglatestet lehetne összeállítani?

(5 pont)

megoldás, statisztika

---

K. 796. Melyik síkidom területe a nagyobb?

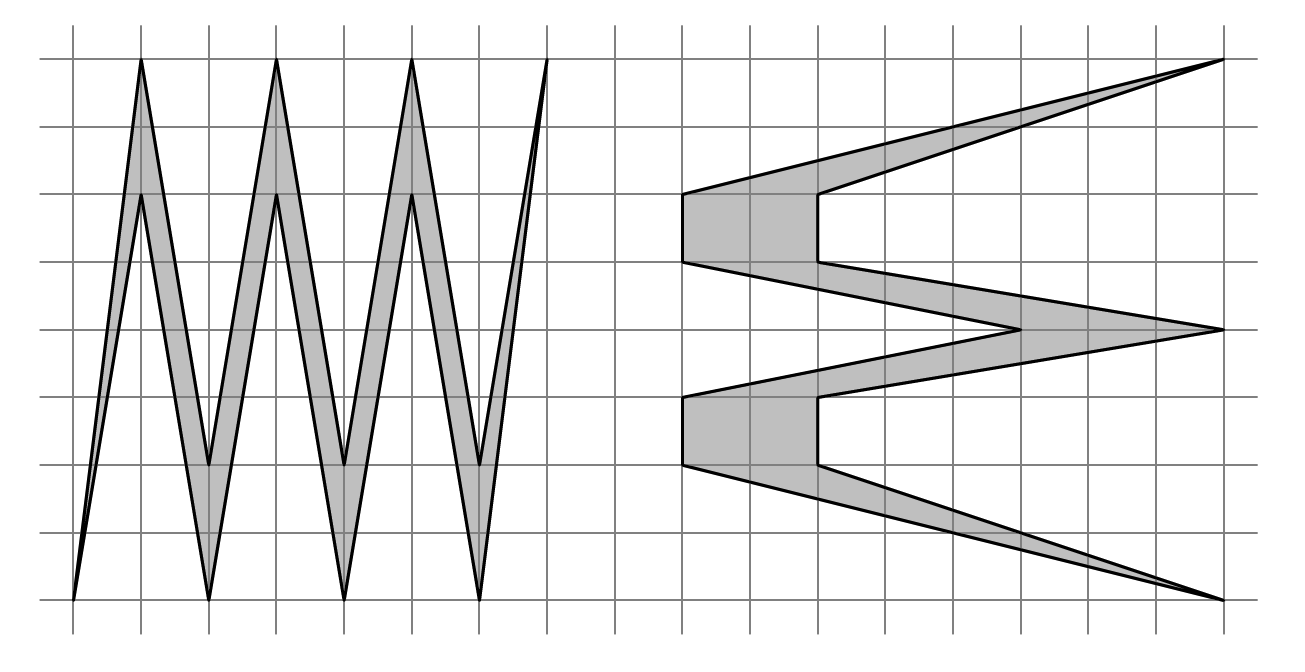
(5 pont)

megoldás, statisztika

K/C-jelű feladatok A beküldési határidő 2024. február 12-én LEJÁRT.

---

K/C. 797. Egy 10 cm befogójú, egyenlő szárú derékszögű háromszög befogói és átfogói mint átmérők fölé rajzolunk egy-egy kört. Az egyik körlapot kiszínezzük pirosra, a másikat kékre, a harmadikat zöldre. Mennyi a területe a legalább két színnel színezett síkrésznek?

(5 pont)

megoldás, statisztika

---

K/C. 798. Kovácsék bejárati ajtaja \(\displaystyle 2\) méter magas és \(\displaystyle 1\) méter széles. Az ajtó fölött a padlótól számított \(\displaystyle 3\) méteres magasságban egy \(\displaystyle 1\) méterre kinyúló vízszintes, téglalap alakú előtető van, amely pont olyan széles, mint az ajtó. Ennek az előtetőnek az ajtótól távolabbi szélén középre rögzítettek egy minden irányba világító lámpát. Mekkora területű részt világít meg a padlón a lámpa az ajtónyíláson keresztül, ha az ajtót teljesen kinyitják? (Az előszoba, melybe az ajtó nyílik, elegendően széles és hosszú ahhoz, hogy az ajtónyílás képe teljes egészében a padlón legyen.)

(5 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2024. február 12-én LEJÁRT.

---

C. 1793. A valós számok halmazán értelmezett \(\displaystyle f\) függvényre az alábbi két feltétel mindegyike teljesül (bármely \(\displaystyle x \in \mathbb{R}\)-re):

\(\displaystyle (1) \)

\(\displaystyle f(x)=f(147-x),\)

\(\displaystyle (2) \)

\(\displaystyle f(x+100)=f(46-x).\)

Határozzuk meg \(\displaystyle f(200)+f(201)+f(202)\) értékét, ha tudjuk, hogy

\(\displaystyle f(50)+f(51)+f(52)+f(53)=2024. \)

Javasolta: Kozma Katalin Abigél (Győr)

(5 pont)

megoldás, statisztika

---

C. 1794. A \(\displaystyle k_1\) és \(\displaystyle k_2\) körök az \(\displaystyle A\), a \(\displaystyle k_2\) és \(\displaystyle k_3\) körök a \(\displaystyle B\), végül a \(\displaystyle k_3\) és \(\displaystyle k_1\) körök a \(\displaystyle C\) pontban páronként kívülről érintik egymást. Az \(\displaystyle AB\) egyenes a \(\displaystyle k_3\) kört másodszor a \(\displaystyle D\) pontban metszi. Bizonyítsuk be, hogy \(\displaystyle AC\) és \(\displaystyle CD\) merőlegesek egymásra.

(Német versenyfeladat)

(5 pont)

megoldás, statisztika

---

C. 1795. Legyen \(\displaystyle p\) valós paraméter. A \(\displaystyle p\) értékeitől függően hány megoldása van az alábbi egyenletnek?

\(\displaystyle |x^2-6x+5|=px^2-6px+9p+4. \)

Javasolta: Szmerka Gergely (Budapest)

(5 pont)

megoldás, statisztika

---

C. 1796. Egy egységnyi élű szabályos oktaédert az egyik háromszöglapjával a lap síkjára helyezünk. Mekkora távolságra vannak ettől a síktól az oktaédernek a síkra nem illeszkedő csúcsai?

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

---

C. 1797. Melyik az a legnagyobb \(\displaystyle x\) egész szám, amelyre \(\displaystyle x>2\), és \(\displaystyle \log_2(x)\), \(\displaystyle \log_4(2x)\) és \(\displaystyle \log_8(3x)\) egy háromszög oldalhosszai lehetnek?

Javasolta: Bíró Bálint (Eger)

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2024. február 12-én LEJÁRT.

---

B. 5358. Legfeljebb hány különböző egész számot lehet megadni úgy, hogy közülük bármely kettő összege kettőhatvány (a 2-nek nemnegatív egész kivetős hatványa) legyen?

Javasolta: Hujter Bálint (Budapest)

(3 pont)

megoldás, statisztika

---

B. 5359. \(\displaystyle a)\) Van-e olyan háromszög, amelyben minden oldal hossza egész, és a területe kisebb, mint \(\displaystyle 1/10\)?

\(\displaystyle b)\) Van-e olyan négyszög, amelyben minden oldal hossza egész, és a területe kisebb, mint \(\displaystyle 1/10\)?

Javasolta: Vígh Viktor (Sándorfalva)

(3 pont)

megoldás, statisztika

---

B. 5360. A nem egyenlő szárú \(\displaystyle ABC\) háromszög legnagyobb szöge \(\displaystyle C\)-nél van. Jelölje a \(\displaystyle C\)-ből induló magasság talppontját \(\displaystyle T\), míg az \(\displaystyle C\)-ből induló belső szögfelező messe az \(\displaystyle AB\) oldalt az \(\displaystyle F\) pontban. Bizonyítsuk be, hogy \(\displaystyle \dfrac{AT}{TB}=\left(\dfrac{AF}{FB}\right)^2\) akkor és csak akkor teljesül, ha \(\displaystyle ACB\sphericalangle=90^\circ\).

Javasolta: Hujter Mihály (Budapest) ötlete alapján

(4 pont)

megoldás, statisztika

---

B. 5361. Jelölje \(\displaystyle a_n\) azt, hogy \(\displaystyle 2n\) hányféleképpen áll elő két pozitív prím összegeként. Igaz-e, hogy az \(\displaystyle (a_n)\) sorozat valahonnan kezdve szigorúan monoton növekedő?

Javasolta: Pach Péter Pál (Budapest)

(4 pont)

megoldás, statisztika

---

B. 5362. Az \(\displaystyle ABC\) háromszögben \(\displaystyle BAC\sphericalangle=50^\circ\) és \(\displaystyle ABC\sphericalangle=70^\circ\). Az \(\displaystyle AC\) és \(\displaystyle BC\) oldalakon felvesszük az \(\displaystyle E\) és \(\displaystyle D\) pontokat úgy, hogy \(\displaystyle ABE\sphericalangle=BAD\sphericalangle= 30^\circ\). Az \(\displaystyle AD\) és \(\displaystyle BE\) szakaszok metszéspontja \(\displaystyle M\). Számítsuk ki az \(\displaystyle ACM\sphericalangle\) és a \(\displaystyle BED\sphericalangle\) szögeket.

Javasolta: Róka Sándor (Nyíregyháza)

(4 pont)

megoldás, statisztika

---

B. 5363. Egy szabályos négyoldalú gúla alaplapja az \(\displaystyle ABCD\) négyzet, a gúla csúcsa az \(\displaystyle E\) pont. Legyen a \(\displaystyle CE\) oldalél felezőpontja az \(\displaystyle F\), a \(\displaystyle BE\) oldalél \(\displaystyle B\)-hez közelebbi harmadolópontja pedig a \(\displaystyle H\) pont. Milyen arányban osztja ketté az \(\displaystyle ABCDE\) gúla térfogatát az \(\displaystyle AHF\) sík?

Javasolta: Kiss Géza (Csömör)

(5 pont)

megoldás, statisztika

---

B. 5364. Egy érme két oldalára az 1, 2, egy kocka lapjaira pedig az 1, 2, 3, 4, 5, 6 számokat írjuk. Határozzuk meg az érme és a kocka összes olyan cinkelését, hogy azokat egyszerre feldobva a 2, \(\displaystyle \ldots\), 8 dobásösszegek mindegyike ugyanolyan valószínűséggel forduljon elő, mint két olyan szabályos tetraéderrel történő dobás esetén, amelyek lapjaira az 1, 2, 3, 4 számokat írjuk. (Tetraéderrel való dobás eredményén az alsó lapon lévő számot értjük; cinkelés alatt pedig azt, hogy egy tárgy súlyozását megváltoztathatjuk úgy, hogy ne feltétlenül egyenlő eséllyel essen a különböző oldalakra.)

Javasolta: Barczy Mátyás (Szeged) és Nyul Gábor (Debrecen)

(6 pont)

megoldás, statisztika

---

B. 5365. Határozzuk meg a legkisebb \(\displaystyle \alpha\) valós számot, amelyhez végtelen sok olyan \(\displaystyle n\) pozitív egész számot lehet találni, amelyre \(\displaystyle \sqrt{13}\cdot n\) és a hozzá legközelebbi egész szám különbsége kisebb, mint \(\displaystyle \alpha /n\).

Javasolta: Somogyi Ákos (London)

(6 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2024. február 12-én LEJÁRT.

---

A. 869. Legyenek \(\displaystyle A\) és \(\displaystyle B\) adott valós számok. A \(\displaystyle 0\le x_1\le x_2\le\dots\le x_n\) valós számok összege \(\displaystyle A\), a \(\displaystyle 0\le y_1\le y_2\le\dots\le y_n\) valós számok összege \(\displaystyle B\).

Mi \(\displaystyle {\sum_{i=1}^n (x_i-y_i)^2}\) lehetséges legnagyobb értéke?

Javasolta: Csikvári Péter (Budapest)

(7 pont)

megoldás, statisztika

---

A. 870. Egy egyszerű gráf minden élére ráírjuk az él két végpontja fokszámainak különbségét. Egy \(\displaystyle N\) csúcsú gráfban legfeljebb mennyi lehet az élekre írt számok összege?

Javasolta: Lenger Dániel és Szűcs Gábor (Budapest)

(7 pont)

megoldás, statisztika

---

A. 871. Az \(\displaystyle ABC\) tompaszögű háromszögnek \(\displaystyle H\) a magasságpontja. Jelölje \(\displaystyle \omega_A\) az \(\displaystyle A\) középpontú, \(\displaystyle AH\) sugarú kört, \(\displaystyle \omega_B\) és \(\displaystyle \omega_C\) hasonlóan vannak definiálva. Az \(\displaystyle ABC\) háromszög síkjának minden \(\displaystyle X\) pontjára definiáljuk az \(\displaystyle \Omega(X)\) kört a következőképpen (ha értelmezhető): vegyük \(\displaystyle X\) polárisait az \(\displaystyle \omega_A\), \(\displaystyle \omega_B\) és \(\displaystyle \omega_C\) körökre nézve, és legyen \(\displaystyle \Omega(X)\) a három egyenes által alkotott háromszög körülírt köre.

Keressük meg (esetleg véges sok kivétellel) azoknak az \(\displaystyle X\) pontoknak a halmazát a síkon, amelyekre \(\displaystyle X\) rajta van \(\displaystyle \Omega(X)\)-en.

Javasolta: Molnár-Szabó Vilmos (Budapest)

(7 pont)

megoldás, statisztika