A KöMaL 2024. áprilisi matematika feladatai

K-jelű feladatok A beküldési határidő: 2024. május 10.. 24:00 (UTC+02:00).

K. 809. Legyen \(\displaystyle a_1\) egy pozitív egész szám, amelyből létrehozunk egy sorozatot a következő szabály szerint. A sorozat első tagját (\(\displaystyle a_1\)) felírjuk – a tízes számrendszerbeli alakját felhasználva – \(\displaystyle a_1=10A_1+b_1\) alakban, ahol \(\displaystyle b_1\) az egyesek helyén álló számjegy. Ebből kiindulva képezzük a sorozat további tagjait az \(\displaystyle a_{n+1}={A_n+6b_n}\) szabály szerint. Igazoljuk, hogy az így képzett sorozatra teljesül, hogy vagy mindegyik tagja osztható \(\displaystyle 59\)-cel, vagy egyik sem.

Urbán János (Budapest) (1939–2012) feladata alapján

(5 pont)

Ezt a feladatot csak 9. osztályosok küldhetik be.

K. 810. Az \(\displaystyle ABCD\) trapézban \(\displaystyle AB\parallel CD\) és \(\displaystyle AB=3CD\), valamint \(\displaystyle CD=DA\). Határozzuk meg a trapéz szögeit, ha tudjuk, hogy \(\displaystyle CDA\sphericalangle=120^{\circ}\).

német versenyfeladat

(5 pont)

Ezt a feladatot csak 9. osztályosok küldhetik be.

K. 811. Egy \(\displaystyle 8\times8\)-as sakktáblára ráírtuk a pozitív egész számokat \(\displaystyle 1\)-től \(\displaystyle 64\)-ig növekvő sorrendben, a bal felső sarokban kezdve és soronként haladva. Lehetséges-e két egymással élben vagy csúcsban szomszédos mezőn álló számot a tábláról törölnünk úgy, hogy a fennmaradó számok összege éppen \(\displaystyle 2024\) legyen?

Javasolta: Bíró Bálint (Eger)

(5 pont)

Ezt a feladatot csak 9. osztályosok küldhetik be.

K/C-jelű feladatok A beküldési határidő: 2024. május 10.. 24:00 (UTC+02:00).

K/C. 812. A \(\displaystyle 2024\)-nek pontosan egy olyan számjegye van (nevezetesen a 0), amely minden számjegyének többszöröse. Hány olyan négyjegyű, pozitív egész szám van, amelynek legalább két ilyen számjegye van?

Javasolta: Kozma Katalin Abigél (Győr)

(5 pont)

Ezt a feladatot csak 1–10. osztályosok küldhetik be.

K/C. 813. Az \(\displaystyle ABCD\) négyzet mellé rajzoltuk az \(\displaystyle EBFG\) négyzetet, mellé pedig több, vele egybevágó négyzetet az alábbi ábra szerint.

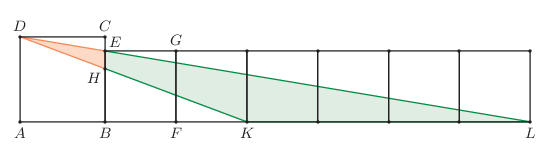
Határozzuk meg a \(\displaystyle DHE\) háromszög és \(\displaystyle HKLE\) négyszög területének arányát.

Deres János (Csurgó) ötletéből

(5 pont)

Ezt a feladatot csak 1–10. osztályosok küldhetik be.

C-jelű feladatok A beküldési határidő: 2024. május 10.. 24:00 (UTC+02:00).

C. 1808. Boglárka egy 4-szer 4-es négyzetháló minden négyzetébe beír a \(\displaystyle 2023\), \(\displaystyle 2024\), \(\displaystyle 2025\) számok közül pontosan egyet. Hány különböző módon teheti ezt meg úgy, hogy minden sorban és minden oszlopban az oda beírt négy darab szám összege osztható legyen \(\displaystyle 3\)-mal?

Javasolta: Kozma Katalin Abigél (Győr)

(5 pont)

C. 1809. Legyen az \(\displaystyle AC\) szakasz belső pontja \(\displaystyle B\), és az \(\displaystyle ABS_1\), a \(\displaystyle BCS_2\) és az \(\displaystyle CAS_3\) olyan egyenlő szárú háromszögek, amelyek közül semelyik kettőnek nincs közös belső pontja, és amelyeknek alapjai az \(\displaystyle AB\), a \(\displaystyle BC\) és az \(\displaystyle CA\), és az alapon fekvő szögeik mind \(\displaystyle 30^{\circ}\)-osak.

Bizonyítsuk be, hogy az \(\displaystyle S_1S_2S_3\) háromszög szabályos.

német versenyfeladat

(5 pont)

C. 1810. Határozzuk meg az \(\displaystyle (x+2)^6+(x^2-4x-4)^3=8x^6\) egyenlet valós megoldásait.

Javasolta: Bíró Bálint (Eger)

(5 pont)

C. 1811. Legyen \(\displaystyle f(x)=x^2\) és \(\displaystyle g(x)=x^2-2x+2\). Határozzuk meg a két függvénygrafikon közös érintőjének egyenletét.

Javasolta: Sándor Csaba (Budapest)

(5 pont)

Ezt a feladatot csak 11–12. osztályosok küldhetik be.

C. 1812. Legyenek egy háromszög oldalhosszai \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), amelyekre teljesül, hogy \(\displaystyle a+b=3c\). Az \(\displaystyle a\), illetve \(\displaystyle b\) oldalakkal szemközti szögek \(\displaystyle \alpha\), illetve \(\displaystyle \beta\). Bizonyítsuk be, hogy \(\displaystyle \ctg{\frac{\alpha}{2}}\cdot{\ctg{\frac{\beta}{2}}}=2.\)

horvát versenyfeladat

(5 pont)

Ezt a feladatot csak 11–12. osztályosok küldhetik be.

B-jelű feladatok A beküldési határidő: 2024. május 10.. 24:00 (UTC+02:00).

B. 5382. Döntsük el, hogy vannak-e olyan \(\displaystyle 2<p<q\) prímszámok, amelyekre a \(\displaystyle \{{p+1}, {p+2}, \ldots, {q-1}\}\) halmaz elemeinek több mint egyharmadrésze prímszám.

Javasolta: Hujter Bálint (Budapest)

(3 pont)

B. 5383. Az \(\displaystyle ABCD\) húrnégyszögben \(\displaystyle BAD\sphericalangle = 90^{\circ}\), \(\displaystyle BC = CD\) és \(\displaystyle AC = 1\). Kiszámítandó a húrnégyszög területe.

Javasolta: Hujter Mihály (Budapest)

(3 pont)

B. 5384. Bizonyítsuk be, hogy ha \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c>0\) és \(\displaystyle a^2+b^2+c^2=abc\), akkor

\(\displaystyle 2(a+b+c)+\dfrac{a^3}{bc}+\dfrac{b^3}{ca}+\dfrac{c^3}{ab} \le abc. \)

Javasolta: Bencze Mihály (Brassó)

(4 pont)

B. 5385. Az \(\displaystyle ABC\) hegyesszögű háromszögben jelölje \(\displaystyle F\) a Feuerbach-kör középpontját. Bizonyítsuk be, hogy \(\displaystyle AF^2-BF^2=Rc\sin(\beta-\alpha)\), ahol \(\displaystyle R\) a köréírt kör sugarát, \(\displaystyle c\) az \(\displaystyle AB\) oldal hosszát, míg \(\displaystyle \alpha\) és \(\displaystyle \beta\) az \(\displaystyle A\) és \(\displaystyle B\) csúcsoknál levő belső szöget jelöli.

Javasolta: Bencze Mihály (Brassó)

(4 pont)

B. 5386. Anna és Balázs a következő játékot játssza. Anna 101-szer, míg Balázs 10-szer dob fel egy szabályos pénzérmét. Anna győz, ha több, mint 10-szer annyi fejet dobott, mint Balázs, különben Balázs nyer. Kinek kedvezőbb ez a játék?

Javasolta: Sztranyák Attila (Budapest)

(5 pont)

B. 5387. A sík véges sok pontját megjelöltük a piros, kék és zöld színek valamelyikével úgy, hogy nincs három kollineáris, azonos színű pont, de bármely két azonos színű pontot összekötő szakaszon van olyan megjelölt pont, amelynek színe különbözik a végpontok színétől. Legfeljebb hány pontot vehettünk fel?

Javasolta: Róka Sándor (Nyíregyháza)

(5 pont)

B. 5388. Mutassuk meg, hogy bármely \(\displaystyle 2n\) egymást követő pozitív egész számot legalább \(\displaystyle n!\)-féleképpen lehet \(\displaystyle n\) párba állítani úgy, hogy semelyik párban ne legyen a számok szorzata négyzetszám.

Javasolta: Róka Sándor (Nyíregyháza)

(6 pont)

B. 5389. Az \(\displaystyle ABC\) hegyesszögű háromszög beírt körének középpontja \(\displaystyle I\), a \(\displaystyle BC\) és \(\displaystyle AC\) oldalakkal vett érintési pontjai \(\displaystyle D\), illetve \(\displaystyle E\), továbbá jelölje \(\displaystyle H\) a háromszög magasságpontját. Igazoljuk, hogy ha \(\displaystyle H\) a \(\displaystyle DE\) szakaszon van, akkor a \(\displaystyle HI\) egyenes felezi az \(\displaystyle AB\) oldalt.

Javasolta: Varga Boldizsár (Budapest)

(6 pont)

A-jelű feladatok A beküldési határidő: 2024. május 10.. 24:00 (UTC+02:00).

A. 878. Legyen \(\displaystyle A\) a \(\displaystyle c\) és \(\displaystyle k\) körök egyik metszéspontja. Legyen \(\displaystyle X_1\) és \(\displaystyle X_2\) tetszőleges pont a \(\displaystyle c\) körön. Jelölje \(\displaystyle Y_i\) az \(\displaystyle AX_i\) egyenes második metszéspontját a \(\displaystyle k\) körrel \(\displaystyle i=1,2\) esetén. Legyen \(\displaystyle P_1\), \(\displaystyle P_2\) és \(\displaystyle P_3\) tetszőleges pont a \(\displaystyle k\) körön, és jelölje \(\displaystyle O\) a \(\displaystyle k\) kör középpontját.

Jelölje \(\displaystyle K_{ij}\) az \(\displaystyle X_iY_iP_j\) háromszög körülírt körének középpontját \(\displaystyle i=1\), \(\displaystyle 2\) és \(\displaystyle {j=1}\), \(\displaystyle 2\), \(\displaystyle 3\) esetén. Legyen \(\displaystyle L_j\) az \(\displaystyle OK_{1j}K_{2j}\) háromszög körülírt körének középpontja \(\displaystyle j=1\), \(\displaystyle 2\), \(\displaystyle 3\) esetén. Bizonyítsuk be, hogy \(\displaystyle L_1\), \(\displaystyle L_2\) és \(\displaystyle L_3\) egy egyenesre esik.

Javasolta: Molnár-Szabó Vilmos (Budapest)

(7 pont)

A. 879. Adott egy \(\displaystyle k>2\) egész szám. Xavér és Yvett a következő játékot játssza. Eredetileg a táblán egy \(\displaystyle n>k\) egész szám szerepel. Ezt követően felváltva lépnek, Xavér kezd. Egy lépés abból áll, hogy a táblán szereplő \(\displaystyle m\) számot kicserélik egy olyan \(\displaystyle m'\) számra, amelyre \(\displaystyle k\le m'<m\) és \(\displaystyle (m',m)=1\). Aki először nem tud lépni, veszít.

Azt mondjuk, hogy egy \(\displaystyle n>k\) egész szám jó, ha Yvettnek van nyerő stratégiája. Mutassuk meg, hogy ha \(\displaystyle n\), \(\displaystyle n'>k\) olyanok, hogy minden \(\displaystyle p\le k\) prímre \(\displaystyle p\) akkor és csak akkor osztja \(\displaystyle n\)-et, ha \(\displaystyle n'\)-t, akkor \(\displaystyle n\) akkor és csak akkor jó, ha \(\displaystyle n'\) jó.

(7 pont)

A. 880. Határozzuk meg az összes \(\displaystyle (a,b,c)\) valós számokból álló számhármast, amelyre létezik olyan \(\displaystyle f\colon\mathbb{Z}^+ \to \mathbb{Z}^+\) függvény, hogy

\(\displaystyle af(n)+bf(n+1)+cf(n+2)<0 \)

minden \(\displaystyle n \in \mathbb{Z}^+\) számra (\(\displaystyle \mathbb{Z}^+\) a pozitív egész számok halmazát jelöli).

Javasolta: Imolay András (Budapest)

(7 pont)