A KöMaL 2024. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2024. június 17-én LEJÁRT. |
M. 432. Készítsünk két, szájával összefordított PET palackból és búzadarából ,,homokórát''. A palackok közé helyezzünk különböző szűkítőket, amelyekkel a kör alakú nyílás \(\displaystyle d\) átmérőjét tudjuk változtatni. Mérjük meg a búzadara \(\displaystyle T\) lepergési idejét a \(\displaystyle d\) átmérő függvényében! Az elméleti várakozás szerint \(\displaystyle T\sim d^\gamma\). Milyen \(\displaystyle \gamma\) kitevő adódik a mérésből?
Közli: Széchenyi Gábor, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2024. június 17-én LEJÁRT. |
G. 853. Egy rendőrautó az autópályán halad. Sebességét a számítógépes rendszer rögzítette, ez alapján készült az alábbi \(\displaystyle v_\mathrm{r}(t)\) grafikon. Egy motoros egyszer csak megelőzi a rendőrautót, a rendőrautó méri a motoros sebességét. Az \(\displaystyle u_\mathrm{m}(t)\) grafikon azt mutatja, hogy mekkora a motoros sebessége a rendőrautóhoz viszonyítva.


\(\displaystyle a)\) Rajzoljuk meg a motoros földhöz viszonyított sebességének \(\displaystyle v_\mathrm{m}(t)\) grafikonját!
\(\displaystyle b)\) A grafikonokon ábrázolt időtartam alatt mikor volt a legtávolabb egymástól a két jármű? Mekkora ez a távolság?
\(\displaystyle c)\) A 60. másodperc után állandó sebességgel haladnak tovább. Mikor előzi vissza a rendőrautó a motorost?
Közli: Baranyai Klára, Veresegyház
(4 pont)
G. 854. Egy gömb alakú léggömbbe a levegőnél kisebb sűrűségű gázt töltöttek. A léggömbről lelógó spárgának a végére gemkapcsokat akasztgatunk abból a célból, hogy a léggömb a teremben egy adott magasságban lebegjen. A lebegést nem sikerült megvalósítani, mert a léggömb, ha 7 gemkapcsot akasztottunk a spárga végére, felemelkedett, de ha 8-at, akkor lesüllyedt. Mekkora lehet a léggömbben lévő gáz sűrűsége? A teremben a levegő sűrűsége \(\displaystyle 1{,}20~\tfrac{\mathrm{kg}}{\mathrm{m}^3}\). A léggömb átmérője \(\displaystyle 26~\mathrm{cm}\), tömege felfújatlan állapotban \(\displaystyle 3~\mathrm{g}\). A spárga tömege \(\displaystyle 2~\mathrm{g}\), egy gemkapocs tömege \(\displaystyle 0{,}6~\mathrm{g}\). A léggömb anyagának vastagságától, a spárga és a gemkapcsok térfogatától eltekinthetünk!
Tarján Imre Országos Emlékverseny, Szolnok
(4 pont)
G. 855. Newton nem a szokásos alakjában \(\displaystyle \left(\tfrac{1}{t}+\tfrac{1}{k}=\tfrac{1}{f}\right)\) írta fel a leképezési törvényt. Ő a tárgyoldali fókuszponttól mérte az \(\displaystyle x_\mathrm{t}\) fókuszontúli tárgytávolságot, illetve a képoldali fókuszponttól mérte az \(\displaystyle x_\mathrm{k}\) fókuszontúli képtávolságot, ahogy ez az ábrán látható.
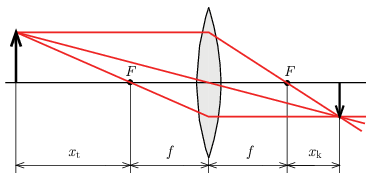
\(\displaystyle a)\) Adjuk meg a legegyszerűbb alakban a leképezési törvényt ezekkel a paraméterekkel!
\(\displaystyle b)\) Hogyan alkalmazható ez a képlet szórólencsékre?
(4 pont)
G. 856. Budapesten mikor delel magasabban a Hold, egy decemberi vagy egy júniusi holdtölte idején?
(4 pont)
 |
P-jelű feladatokA beküldési határidő 2024. június 17-én LEJÁRT. |
P. 5571. Egy \(\displaystyle h\) magasságú asztal sarka felett ugyancsak \(\displaystyle h\) magasságból egy kicsiny golyót ejtünk el. Az asztal sarkától legfeljebb milyen távol érkezhet a golyó a talajra? Az ütközést tekintsük tökéletesen rugalmasnak.
Közli: Simon Péter, Pécs
(5 pont)
P. 5572. A 60 kg tömegű Aladár egy (a vízszinttől számítva) 50 m magas hídról ,,halálugrásra'' (bungee jumping ugrásra) vállalkozik. A kötél hosszát úgy állították be, hogy Aladár az ugrás során éppen érintse a vízfelszínt. Így az igen könnyű, de kellőképpen rugalmas kötelének direkciós állandója 72 N/m. A 80 kg-os Bendegúz is vállalkozik egy hasonló ugrásra. Az ő kötele is ugyanolyan minőségű, mint Aladáré, de rövidebb annál.
\(\displaystyle a)\) Milyen hosszú Aladár, illetve Bendegúz kötele? Mekkora Bendegúz kötelének direkciós állandója?
\(\displaystyle b)\) Mekkora Aladár, illetve Bendegúz maximális gyorsulása?
\(\displaystyle c)\) Melyikük éri el hamarabb a vízfelszínt, ha egyszerre ugranak le a hídról?
Feltételezhetjük, hogy a kötelek megnyúlása egyenesen arányos a nyújtóerővel. Az ugrók testmagasságát és a közegellenállást ne vegyük számításba.
Közli: Szabó Endre, Vágfüzes, Szlovákia
(5 pont)
P. 5573. Egy \(\displaystyle 30^\circ\)-os hajlásszögű lejtőre homogén hengert helyeztünk, amelyet a tömegközéppontja feletti legmagasabb pontjánál egy vízszintes fonállal az ábrán látható módon a lejtőhöz kötöttünk. Legalább mekkora legyen a henger és a lejtő között a súrlódási együttható, hogy a henger ebben a helyzetben nyugalomban maradhasson?
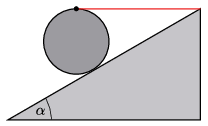
Közli: Holics László, Budapest
(4 pont)
P. 5574. Alul zárt, függőleges, hőszigetelt hengerben lévő dugattyúk azonos hőmérsékletű és térfogatú nitrogént zárnak el. Kezdetben a hőmérséklet \(\displaystyle T_1=300~\mathrm{K}\). A felső dugattyú súrlódásmentesen mozoghat, a tömege \(\displaystyle m=40~\mathrm{kg}\), az alsó jó hővezető anyagból készült és rögzített, a felső hőszigetelt. A külső légnyomás \(\displaystyle 10^5~\mathrm{Pa}\), az alsó gáz nyomása \(\displaystyle 1{,}2\cdot 10^5~\mathrm{Pa}\), a henger alapterülete \(\displaystyle A=1~\mathrm{dm^2}\), \(\displaystyle h=0{,}5~\mathrm{m}\).
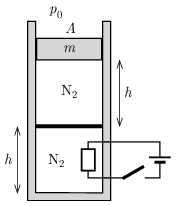
\(\displaystyle a)\) Mennyi a felső és az alsó részben lévő nitrogén tömege?
A fűtőszál \(\displaystyle Q=1580~\mathrm{J}\) hőt közöl a rendszerrel.
\(\displaystyle b)\) Mennyivel változik meg a felső és az alsó gáz belső energiája?
\(\displaystyle c)\) Mennyivel változik meg a felső gáz térfogata?
Közli: Veres Dénes, Szolnok
(4 pont)
P. 5575. Nagy méretű, földelt fémlap felett \(\displaystyle h\) magasságban egy kicsiny elektromos dipólust helyezünk el. Mindezt úgy tesszük, hogy annak \(\displaystyle \boldsymbol{p}\) dipólmomentuma az ábrán látott módon felfelé mutasson.
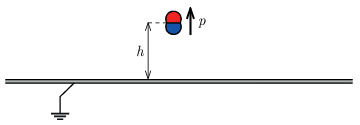
Határozzuk meg a fémlapon azon pontok helyét, ahol a felületi töltéssűrűség zérus!
Közli: Németh Róbert, Budapest
(5 pont)
P. 5576. Tegyük fel, hogy rendelkezünk olyan mérőműszerekkel, amelyek nemcsak szinuszos váltóáram, illetve váltófeszültség effektív értékét mérik, hanem tetszőleges periodikus jelekét is.
\(\displaystyle a)\) Csatlakoztassunk egy \(\displaystyle f=1/T\) frekvenciájú, szimmetrikus négyszögjelet szolgáltató feszültséggenerátorra egy ideális induktivitást, amelynek önindukciós együtthatója \(\displaystyle L\). Ideális feszültség- és árammérő műszerekkel megmérjük az induktivitás áramának effektív értékét, illetve a feszültséggenerátor feszültségének effektív értékét. Mit mutatnak a műszerek, ha a négyszögjel lefutását a következő ábra mutatja, továbbá tudjuk, hogy a \(\displaystyle t=0\) időpillanatban az induktivitás árama zérus?
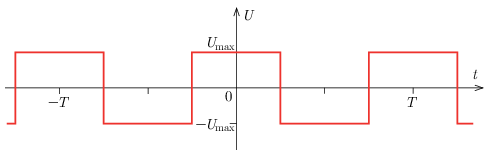
\(\displaystyle b)\) Csatlakoztassunk egy \(\displaystyle f=1/T\) frekvenciájú, szimmetrikus négyszögjelet szolgáltató áramgenerátorra egy ideális kondenzátort, amelynek kapacitása \(\displaystyle C\). Ideális feszültség- és árammérő műszerekkel megmérjük a kondenzátor áramának effektív értékét, illetve a áramgenerátor kimeneti feszültségének effektív értékét. Mit mutatnak a műszerek, ha a négyszögjel lefutását a következő ábra mutatja, továbbá tudjuk, hogy a kondenzátor feszültsége a \(\displaystyle t=0\) időpillanatban zérus?
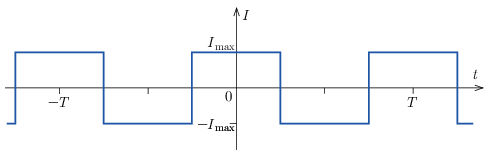
Mit mutatnak a műszerek az \(\displaystyle a)\) és a \(\displaystyle b)\) esetben? A válaszokat \(\displaystyle I_\mathrm{max}\), \(\displaystyle U_\mathrm{max}\), \(\displaystyle L\), \(\displaystyle C\) és \(\displaystyle f\) segítségével adjuk meg.
Közli: Honyek Gyula, Veresegyház
(5 pont)
P. 5577. Egy gyűjtőlencse bal oldalára egy pontszerű tárgyat helyeztünk, amelyből kiinduló két sugarat ábrázoltunk a lencsén történő áthaladás után. Az egyik sugár éppen a lencse fókuszpontján halad át. Az ábra alapján szerkesszük meg (körzővel, vonalzóval) a fényforrás helyét! Írjuk le a szerkesztés lépéseit!
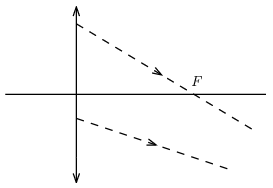
Példatári feladat nyomán
(4 pont)
P. 5578. Az előreláthatóan 2024-ben tetőző, fokozott naptevékenység következtében 2023. november 5-én este rendkívül látványos sarki fényt figyelhettünk meg Magyarországon, amely azonban a sarkvidéken rendszeresen látható égi jelenséggel ellentétben a domináns zöld szín helyett főképp vöröses színben pompázott. Látható fényt feltételezve legfeljebb hány fényjelenséget okozó ütközésre elegendő a napszéllel 2000 km/s sebességgel érkező egyetlen elektron energiája?
Közli: Kenderes Anett, Budapest
(3 pont)
P. 5579. Helsinkiben karácsonykor kicsit több mint 6 és fél perc alatt kel fel a Nap. Mikor lesz ugyanott az év során a legrövidebb ez az időtartam? Hány percig tart Helsinkiben a leggyorsabb napfelkelte?
Helsinki az északi szélesség 60. fokán fekszik, sík területen. A Nap látszólagos átmérője körülbelül fél fok. A földpálya excentricitásából származó kicsiny eltérésekkel és a légkör hatásával ebben a feladatban ne foglalkozzunk.
Közli: Vankó Péter, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
