A KöMaL 2023. márciusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2023. április 11-én LEJÁRT. |
K. 759. Egy kilencfős társaságról tudjuk, hogy mindenki pontosan négy másik embert ismer a társaság tagjai közül. (Az ismeretség kölcsönös.)
\(\displaystyle a)\) Lehetséges-e, hogy a társaság tagjai között bármely két embernek van közös ismerőse?
\(\displaystyle b)\) Igaz-e, hogy egy ilyen társaság tagjai között bármely két ember vagy ismeri egymást, vagy van közös ismerősük?
(5 pont)
K. 760. Az \(\displaystyle A(2;4)\), \(\displaystyle B(6;4)\), \(\displaystyle C(4;10)\) háromszöget az \(\displaystyle x = a\), majd az \(\displaystyle y = 2\) egyenesre tükrözzük.
\(\displaystyle a)\) Mennyi a két tükrözés után kapott csúcsok második koordinátáinak összege?
\(\displaystyle b)\) Mennyi \(\displaystyle a\) értéke, ha a két tükrözés után kapott csúcsok első koordinátáinak összege 36?
(5 pont)
K. 761. Jancsi a 3/5 számlálójához és nevezőjéhez is hozzáírja – vagy elé, vagy mögé – ugyanazt a számjegyet úgy, hogy a számlálóban és a nevezőben is kétjegyű szám szerepeljen. Mekkora a legnagyobb eltérés az így kapható számok között?
(5 pont)
 |
K/C-jelű feladatokA beküldési határidő 2023. április 11-én LEJÁRT. |
K/C. 762. Egy \(\displaystyle 5\times5\)-ös táblázat huszonöt mezőjét valamilyen sorrendben kiválasztjuk, és egy számot írunk rá. Az aktuálisan választott mezőre azt a számot írjuk, amely megmutatja, hogy annak a mezőnek addig hány olyan oldalszomszédja van már, amelyre írtunk számot.
(Ezt a táblázatot pl. az alábbi sorrendben tölthettük ki: a5, b5, c5, d5, e5, e4, e3, e2, a4, a3, a2, a1, b1, c1, d1, e1, \(\displaystyle \ldots\,\).)
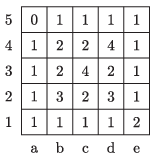
Készítsünk még két ilyen kitöltést. Adjuk össze a kitöltésben lévő számokat.
Bizonyítsuk be, hogy akárhogyan töltjük ki a szabálynak megfelelően a táblázatot, a számok összege minden esetben 40 lesz.
(5 pont)
K/C. 763. Egy egységnyi sugarú félkörbe két olyan, az átmérőre illeszkedő négyzetet írunk, melyeknek van közös oldalszakasza, és egy-egy csúcsuk a körvonalra illeszkedik.
Tudjuk, hogy a kör középpontjából a két négyzet körön lévő csúcsaihoz húzott sugarak egymásra merőlegesek. Igazoljuk, hogy a két, ilyen módon megrajzolt négyzet területének összege állandó.
(5 pont)
 |
C-jelű feladatokA beküldési határidő 2023. április 11-én LEJÁRT. |
C. 1758. Ádám az egyik rejtvényújságban talált egy bűvös négyzetet (tehát olyan \(\displaystyle 3\times3\)-as számnégyzetet, amelyben az egyes sorokban, oszlopokban, illetve a két átlóban található számok összege megegyezik), melyet ki is töltött helyesen, majd találomra kiválasztott egy sort vagy egy oszlopot a táblázatból, és felírta a benne szereplő számokat balról jobbra vagy fentről lefele olvasva. Ezeket a számokat jelölik az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) betűk az így keletkező \(\displaystyle ax^2 + bx + c = 0\) egyenletben. Ádám nagy örömmel vette tudomásul, hogy az egyenletnek két valós gyöke is van. Ezek után kiszámolta az egyenlet gyökeinek négyzetösszegét. Milyen számot kaphatott?
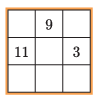
Javasolta: Teleki Olivér (Tököl)
(5 pont)
C. 1759. Egymás mellé helyeztük az \(\displaystyle ABC\) és \(\displaystyle EDC\) derékszögű háromszögeket az ábra szerint.
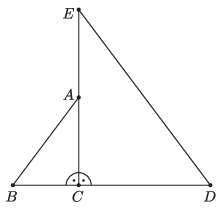
Az \(\displaystyle ABC\) háromszögben \(\displaystyle BC=3\), \(\displaystyle {CA=4}\), az \(\displaystyle EDC\) háromszögben \(\displaystyle DC=6\), \(\displaystyle CE=8\). Az \(\displaystyle ABE\) háromszög körülírt köre a \(\displaystyle DE\) egyenest másodszor a \(\displaystyle P\), a \(\displaystyle DB\) egyenest másodszor a \(\displaystyle Q\) pontban metszi. Határozzuk meg az \(\displaystyle ABDE\) négyszög és az \(\displaystyle AEPQB\) ötszög területe arányának pontos értékét.
Javasolta: Bíró Bálint (Eger)
(5 pont)
C. 1760. Adjuk meg az összes olyan pozitív egész számot, amelyhez a faktoriálisát hozzáadva a szám köbét kapjuk.
(5 pont)
C. 1761. Egy szabályos háromszöget az egyik oldallal párhuzamos egyenessel elvágunk. Megrajzoljuk a keletkező háromszög és a trapéz köré írható két kört. Lehet-e a trapéz és a háromszög köré írt sugarának aránya \(\displaystyle \frac{\sqrt{3}}{3}\)?
Javasolta: Tatár Zsuzsanna Mária (Esztergom)
(5 pont)
C. 1762. Létezik-e olyan pozitív \(\displaystyle p\) prímszám, amelyre teljesül, hogy
\(\displaystyle \log_{p-2}(4p-11)=m, \)
ha az \(\displaystyle m\) paraméter a \(\displaystyle 2023\) valamelyik számjegye?
Javasolta: Bíró Bálint (Eger)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2023. április 11-én LEJÁRT. |
B. 5302. Egy \(\displaystyle 8 \times 8\)-as táblázat minden mezőjébe \(\displaystyle +1\)-et vagy \(\displaystyle -1\)-et írtunk úgy, hogy az összes szám összege 0. Minden sorban és oszlopban kiszámoljuk a számok összegét. Legfeljebb hány pozitív szám lehet ezen 16 összeg között?
Gáspár Merse Előd (Budapest) ötlete nyomán
(3 pont)
B. 5303. Az \(\displaystyle ABC\) egyenlő szárú derékszögű háromszögnek \(\displaystyle C\)-nél van a derékszöge. Vegyünk fel a \(\displaystyle BC\) oldal belsejében egy \(\displaystyle D\) pontot úgy, hogy a \(\displaystyle CDA\) szög \(\displaystyle 75^\circ\) legyen. Tegyük fel, hogy az \(\displaystyle ADC\) háromszög területe egységnyi. Bizonyítsuk be, hogy \(\displaystyle BD = 2\).
Javasolta: Hujter Mihály (Budapest)
(4 pont)
B. 5304. \(\displaystyle a)\) Vannak-e olyan \(\displaystyle a\) és \(\displaystyle b\) pozitív egész számok, amelyekre
\(\displaystyle a+b \mid a^2+b^2, \quad\text{de}\quad a+b \nmid a^4 + b^4? \)
\(\displaystyle b)\) Vannak-e olyan \(\displaystyle a\) és \(\displaystyle b\) pozitív egész számok, amelyekre
\(\displaystyle a+b \mid a^4+b^4, \quad\text{de}\quad a+b \nmid a^2+b^2? \)
Javasolta: Hujter Bálint (Budapest)
(4 pont)
B. 5305. Legyen az \(\displaystyle ABC\) háromszög \(\displaystyle BC\) oldalának \(\displaystyle B\)-hez közelebbi harmadolópontja \(\displaystyle A_1\), \(\displaystyle C\)-hez közelebbi harmadolópontja pedig \(\displaystyle A_2\). A \(\displaystyle CA\) oldalon hasonlóképpen jelöljük ki a \(\displaystyle B_1\) és \(\displaystyle B_2\), végül az \(\displaystyle AB\) oldalon a \(\displaystyle C_1\) és \(\displaystyle C_2\) harmadolópontokat. Bizonyítsuk be, hogy az \(\displaystyle ABC\) háromszög súlypontja illeszkedik az \(\displaystyle A_1B_1C_1\) és \(\displaystyle A_2B_2C_2\) háromszögek körülírt köreinek közös pontjait összekötő egyenesre.
Javasolta: Bíró Bálint (Eger)
(4 pont)
B. 5306. Van egy cinkelt dobókockánk és egy cinkelt érménk, amelynek egyik oldalán egy pötty van, a másik oldalán pedig kettő. Tudjuk, hogy a dobott pöttyök számának várható értéke ugyanannyi a kocka és az érme esetén. Mutassuk meg, hogy egyszerre dobva a kockával és az érmével, annak a valószínűsége, hogy az érmével több pöttyöt dobunk, mint a kockával nagyobb, mint annak a valószínűsége, hogy a kockával dobunk több pöttyöt, mint az érmével.
Javasolta: Vígh Viktor (Sándorfalva)
(5 pont)
B. 5307. Egy hegyesszögű háromszög területe \(\displaystyle T\), beírt körének sugara \(\displaystyle r\), körülírt körének sugara \(\displaystyle R\). Mutassuk meg, hogy
\(\displaystyle \sqrt{3}\,T \le {(r+R)}^2. \)
Javasolta: Simon László Bence (Budapest)
(5 pont)
B. 5308. Jelölje \(\displaystyle a_n\) az \(\displaystyle n+1,n+2,\ldots,n+10\) pozitív egész számok legkisebb közös többszörösét. Határozzuk meg a legnagyobb olyan \(\displaystyle \lambda\) valós számot, melyre \(\displaystyle \lambda a_{n}\le a_{n+1}\) mindig teljesül.
Javasolta: Pach Péter Pál (Budapest)
(6 pont)
B. 5309. Szerkesszük meg a parabola fókuszpontját és vezéregyenesét, ha adott a tengelye és két pontja.
Javasolta: Holló Gábor (Budapest)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2023. április 11-én LEJÁRT. |
A. 848. Legyen \(\displaystyle G\) egy síkgráf, amely egyben páros gráf is. Igaz-e mindig, hogy minden lapjához hozzárendelhetjük egy csúcsát úgy, hogy semelyik két laphoz ne rendeljük ugyanazt a csúcsot?
Javasolta: Matolcsi Dávid (Budapest)
(7 pont)
A. 849. Az \(\displaystyle r\) valós szám esetén jelölje \(\displaystyle f(r)\) az \(\displaystyle r\) számhoz legközelebbi egész számot (ha \(\displaystyle r\) törtrésze \(\displaystyle 1/2\), \(\displaystyle f(r)\) legyen \(\displaystyle r-1/2\)). Legyenek \(\displaystyle a>b>c\) racionális számok úgy, hogy minden \(\displaystyle n\) egészre \(\displaystyle f(na)+f(nb)+f(nc)=n\) teljesüljön. Mi lehet \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle c\) értéke?
Javasolta: Damásdi Gábor (Budapest)
(7 pont)
A. 850. Igazoljuk, hogy létezik egy olyan \(\displaystyle N\) pozitív valós szám, melyre tetszőleges \(\displaystyle a,b>N\) valós számok esetén az \(\displaystyle a\) és \(\displaystyle b\) hosszúságú oldalakkal rendelkező téglalap kerülete lefedhető egymásba nem nyúló egység sugarú körlapokkal (a körlapok érinthetik egymást).
Javasolta: Váli Benedek (Budapest)
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)