A KöMaL 2024. szeptemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2024. október 10-én LEJÁRT. |
K. 819. Kati a táblára felírt \(\displaystyle 10\) darab \(\displaystyle +1\)-et. Egyszerre megváltoztathatja tetszőleges \(\displaystyle 5\) számnak az előjelét (nevezzük ezt egy ,,lépés''-nek). Ezt a változtatást az aktuálisan a táblán levő számok közül tetszőlegesen kiválasztott \(\displaystyle 5\) számmal akárhányszor megteheti. El tudja-e érni azt, hogy a táblán \(\displaystyle 9\) darab \(\displaystyle +1\) és \(\displaystyle 1\) darab \(\displaystyle -1\) szerepeljen? Ha igen, akkor mennyi az ehhez szükséges minimális lépésszám?
(5 pont)
K. 820. A Tóth családban \(\displaystyle 6\) gyerek van. A fiúk átlagéletkora \(\displaystyle 20\) év, a lányoké \(\displaystyle 12\) év, az összes gyereké pedig \(\displaystyle 16\) év. Tudjuk továbbá, hogy minden gyereknek van azonos nemű ikertestvére. Hány évesek a gyerekek külön-külön?
(5 pont)
K. 821. Egy \(\displaystyle 1~\mathrm{m}\) élhosszúságú, kocka alakú, felül nyitott edény aljába egy henger alakú, felül nyitott edényt helyeztek, és azt a kocka alakú edény aljához rögzítették. A kocka alakú edénybe egy csapból egyenletesen folyik a víz a hengeren kívüli részbe. Azt tapasztaljuk, hogy a vízszint a kocka falán \(\displaystyle 10\) percig egyenletesen emelkedik, aztán \(\displaystyle 10\) percre megáll az emelkedése, majd amikor ismét elkezd emelkedni, onnan számítva \(\displaystyle 20\) perc alatt telik meg teljesen a kocka alakú edény. Mekkora a henger alakú edény alapkörének sugara, és mekkora a magassága?
(5 pont)
 |
K/C-jelű feladatokA beküldési határidő 2024. október 10-én LEJÁRT. |
K/C. 822. Kati azt a feladatot kapta, hogy számítsa ki a mellékelt ábrán látható körbe rajzolt ötszög területét. Az oldalak hosszát cm-ben mérve az ábrán jelölték. Kati elvégezte a számításokat, és \(\displaystyle {30+10{,}5\sqrt{30}~\mathrm{cm}^2}\) jött ki neki eredményül. Jól számolt-e Kati?
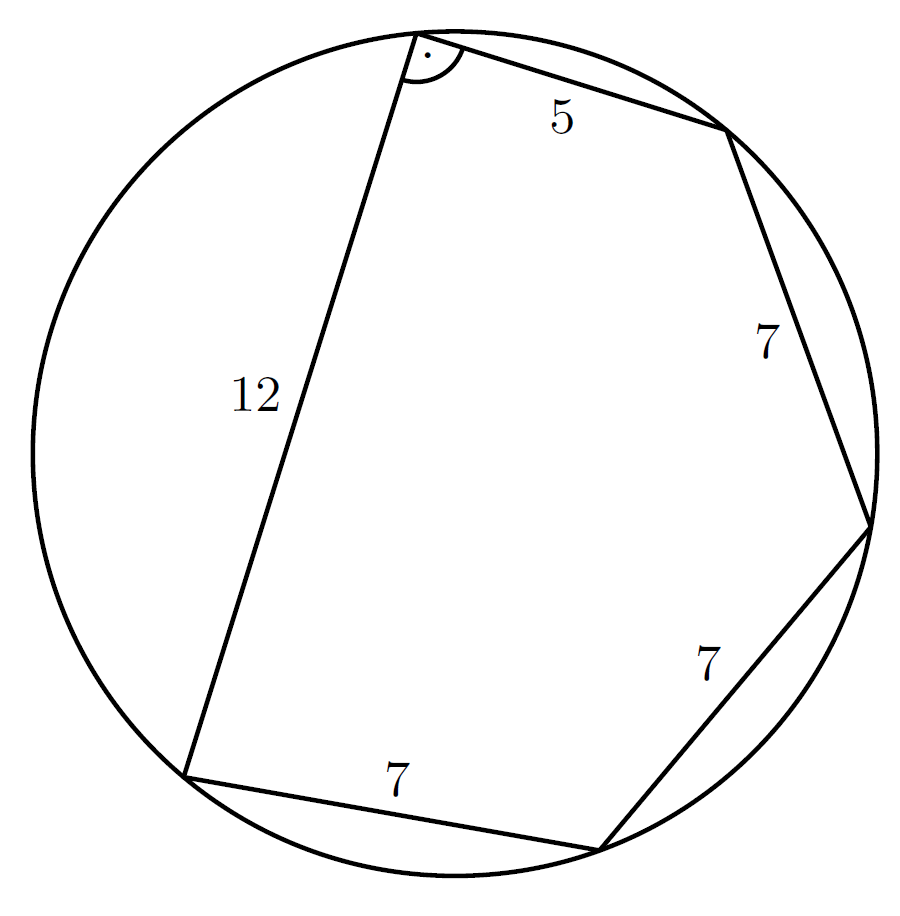
(5 pont)
K/C. 823. Egy konvex \(\displaystyle 2024\)-szög minden oldalegyenesét az adott oldalegyenesre merőleges irányban \(\displaystyle 4\) egységgel eltoljuk kifelé. Így kapunk egy újabb konvex \(\displaystyle 2024\)-szöget. Mutassuk meg, hogy a kapott konvex \(\displaystyle 2024\)-szög kerülete legalább \(\displaystyle 25\) egységnyivel nagyobb, mint az eredeti sokszögé.
(5 pont)
 |
C-jelű feladatokA beküldési határidő 2024. október 10-én LEJÁRT. |
C. 1818. Hány olyan egész számokból álló számötös van, amelyre a
\(\displaystyle \textit{k} \cdot \textit{ö}\cdot \textit{m}\cdot \textit{a}\cdot \textit{l}=-130 \)
egyenlőség teljesül, ha a számok sorrendje is számít?
Javasolta: Kozma Katalin Abigél, Győr
(5 pont)
C. 1819. Legyen \(\displaystyle ABCD\) egységoldalú négyzet, és legyen az \(\displaystyle A\) középpontú \(\displaystyle AC\) sugarú kör \(\displaystyle k\). Legyen \(\displaystyle k\)-nak az \(\displaystyle AB\) félegyenessel \(\displaystyle B\)-n túl vett metszéspontja \(\displaystyle E\), míg az \(\displaystyle AD\) félegyenessel \(\displaystyle D\)-n túl vett metszéspontja \(\displaystyle F\). Messe az \(\displaystyle EF\) egyenes \(\displaystyle BC\)-t \(\displaystyle G\)-ben, és tükrözzük \(\displaystyle B\)-t \(\displaystyle AG\) egyenesre, legyen a tükörkép \(\displaystyle H\). Hány egység hosszú a \(\displaystyle HE\) szakasz?
Javasolta: Hegedűs Dániel, Gyöngyös
(5 pont)
C. 1820. Bizonyítsuk be, hogy ha \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c>0\) és \(\displaystyle a+b+c=1\), akkor
\(\displaystyle a)\) \(\displaystyle \displaystyle{\frac{1-a^2}{b+c}+\frac{1-b^2}{c+a}+\frac{1-c^2}{a+b}=4}\),
\(\displaystyle b)\) \(\displaystyle \displaystyle{\frac{1-a^3}{b+c}+\frac{1-b^3}{c+a}+\frac{1-c^3}{a+b}\geq \frac{13}{3}}\).
Javasolta: Bencze Mihály, Brassó
(5 pont)
C. 1821. Gyula és Gil egy szabályos dobókockával játszik. Ha a dobás eredménye összetett szám, akkor Gil kap egy pontot, egyébként pedig Gyula kap egy pontot. Amikor valamelyikük eléri a hat pontot, a játék befejeződik. Mekkora a valószínűsége, hogy valamelyikük javára éppen \(\displaystyle 6:3\) lesz a végeredmény?
Javasolta: Kozma Katalin Abigél, Győr
(5 pont)
C. 1822. Az \(\displaystyle ABCD\) konvex négyszög \(\displaystyle AC\) és \(\displaystyle BD\) átlói az \(\displaystyle M\) pontban metszik egymást. Az átlók által létrehozott \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\) és \(\displaystyle DAM\) háromszögek területének számértékei rendre az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) pozitív egész számok.
\(\displaystyle a)\) Bizonyítsuk be, hogy \(\displaystyle a\cdot b\cdot c\cdot d\) négyzetszám.
\(\displaystyle b)\) Tegyük fel, hogy az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) számok között pontosan két, egymástól különböző páratlan prímszám van. Határozzuk meg az \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) számokat úgy, hogy az \(\displaystyle ABCD\) négyszög területe a lehető legkisebb négyzetszám legyen.
Javasolta: Bíró Bálint, Eger
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2024. október 10-én LEJÁRT. |
B. 5398. Az \(\displaystyle ABCD\) trapézban \(\displaystyle AB \parallel CD\) és \(\displaystyle ADC \sphericalangle - CBA \sphericalangle = 90^{\circ}\). Igazoljuk, hogy a szárak négyzetének összege egyenlő az alapok különbségének négyzetével.
Javasolta: Oláh Miklós, Szilágykraszna
(3 pont)
B. 5399. Egy ötjegyű négyzetszámnak nincs \(\displaystyle 9\)-es számjegye. Mindegyik számjegyéhez \(\displaystyle 1\)-et hozzáadva ismét négyzetszámot kapunk. Melyik lehet ez a négyzetszám?
Javasolta: Kiss Géza, Csömör
(3 pont)
B. 5400. Egy \(\displaystyle 3\times3\)-as bűvös négyzetben az egyik számot \(\displaystyle 1\)-gyel megnöveltük. Legalább hány számot kell még megváltoztatnunk ahhoz, hogy ismét bűvös négyzetet kapjunk? (A \(\displaystyle 3\times3\)-as bűvös négyzet olyan \(\displaystyle 3\times 3\)-as számtáblázat, amelynek minden sorában, oszlopában és átlójában szereplő három-három szám összege ugyanannyi.)
Javasolta: Juhász Máté
(4 pont)
B. 5401. Legfeljebb mennyi lehet az \(\displaystyle mn\) szorzat értéke, ha \(\displaystyle m\), \(\displaystyle n\) és
\(\displaystyle \sqrt{25+\sqrt{n+\sqrt{m}}}+\sqrt{25-\sqrt{n+\sqrt{m}}} \)
is pozitív egész számok?
Javasolta: Sztranyák Attila, Budapest
(4 pont)
B. 5402. Egy háromszög oldalainak hosszúsága \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\). Tegyük fel, hogy fennáll
\(\displaystyle a^2+b^2+c^2 = a^2b^2c^2. \)
Bizonyítandó, hogy a háromszög területe legfeljebb \(\displaystyle \frac34\), és egyenlőség csak az egyenlő oldalú háromszög esetében lehetséges.
Javasolta: Hujter Mihály, Budapest
(5 pont)
B. 5403. Tegyük fel, hogy egy egyszerű, összefüggő \(\displaystyle k\)-reguláris (\(\displaystyle k \ge 2\)) \(\displaystyle G\) gráf éleit ki lehet színezni \(\displaystyle k\) színnel úgy, hogy minden csúcsban csupa különböző színű él találkozzon. Bizonyítsuk be, hogy \(\displaystyle G\) bármelyik élét törölve a kapott gráf is összefüggő.
Javasolta: Hujter Bálint, Budapest
(5 pont)
B. 5404. Az \(\displaystyle ABC\) hegyesszögű háromszög magasságainak talppontjai \(\displaystyle T_A\), \(\displaystyle T_B\), \(\displaystyle T_C\), továbbá a \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) oldalak felezőpontjai rendre \(\displaystyle F_A\), \(\displaystyle F_B\) és \(\displaystyle F_C\). Jelölje \(\displaystyle r\) a beírt kör sugarát. Legyen \(\displaystyle P_A\) az \(\displaystyle AT_A\) szakasz azon pontja, amelyre \(\displaystyle AP_A = r\). Hasonló módon kapjuk a \(\displaystyle P_B\) és \(\displaystyle P_C\) pontokat. Mutassuk meg, hogy az \(\displaystyle F_AP_A\), \(\displaystyle F_BP_B\), \(\displaystyle F_CP_C\) szakaszok egy pontban metszik egymást.
Javasolta: Kiss Géza, Csömör
(6 pont)
B. 5405. Az \(\displaystyle a_1\), \(\displaystyle a_2\), \(\displaystyle \ldots\), \(\displaystyle a_n\) és \(\displaystyle b_1\), \(\displaystyle b_2\), \(\displaystyle \ldots\), \(\displaystyle b_n\) pozitív egész számokra teljesül, hogy bármely \(\displaystyle i<j\leq n\) indexekre \(\displaystyle b_i\) és \(\displaystyle b_j\) legnagyobb közös osztója nem osztója \(\displaystyle (a_i-a_j)\)-nek. Mutassuk meg, hogy \(\displaystyle \displaystyle \sum_{i=1}^n \frac1{b_i} \leq 1\).
Javasolta: Varga Boldizsár, Budapest
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2024. október 10-én LEJÁRT. |
A. 884. Egy \(\displaystyle n\times n\)-es táblázatot kitöltünk valós számokkal úgy, hogy minden sorban és minden oszlopban 1 legyen a számok összege. \(\displaystyle K\) mely értékeire igaz a következő állítás: ha a táblázatban szereplő negatív számok abszolút értékeinek összege legfeljebb \(\displaystyle K\), akkor biztosan ki lehet választani \(\displaystyle n\) pozitív számot a táblázatból úgy, hogy minden sorból és minden oszlopból pontosan egy számot válasszunk.
Javasolta: Bencsik Dávid, Budapest
(7 pont)
A. 885. Legyen adva egy hegyesszögű nem egyenlőszárú \(\displaystyle ABC\) háromszög. Legyen \(\displaystyle BE\) és \(\displaystyle CF\) a háromszög két magassága, \(\displaystyle D\) pedig jelölje a háromszög beírt körének érintési pontját a \(\displaystyle BC\) oldalon. A \(\displaystyle BDE\) háromszög körülírt köre messe az \(\displaystyle AB\) egyenest másodszor a \(\displaystyle K\) pontban, a \(\displaystyle CDF\) háromszög körülírt köre messe az \(\displaystyle AC\) egyenest másodszor az \(\displaystyle L\) pontban. A \(\displaystyle BDE\) és a \(\displaystyle CDF\) háromszögek körülírt körei a \(\displaystyle KL\) egyenest másodszor rendre az \(\displaystyle X\) és az \(\displaystyle Y\) pontban metszik. Bizonyítandó, hogy a \(\displaystyle DXY\) háromszög beírt körének középpontja az \(\displaystyle ABC\) háromszög beírt körére esik.
Javasolta: Luu Dong, Vietnam
(7 pont)
A. 886. Adottak a \(\displaystyle k\) és \(\displaystyle n\) 1-nél nagyobb különbözô pozitív egész számok, továbbá véges sok (nem feltétlenül különböző) egész szám felírva a táblára. Kázmér egy lépésben letörölheti egy \(\displaystyle k\)-val nem osztható differenciájú számtani sorozat \(\displaystyle k\) egymást követő elemét, míg Nándor letörölheti egy \(\displaystyle n\)-nel nem osztható differenciájú számtani sorozat \(\displaystyle n\) egymást követő elemét. Tudjuk, hogy a kiindulási számok olyanok, hogy Kázmér és Nándor is le tudja törölni az összes számot véges sok lépésben (külön-külön). Bizonyítsuk be, hogy ekkor a táblán szereplő legnagyobb és legkisebb szám különbsége legalább \(\displaystyle \varphi(n)+\varphi(k)\), ahol \(\displaystyle \varphi\) az Euler-féle fí-függvényt jelöli, vagyis \(\displaystyle \varphi(n)\) az \(\displaystyle n\)-nél nem nagyobb, \(\displaystyle n\)-hez relatív prím pozitív egészek száma.
Javasolta: Varga Boldizsár, Budapest
(7 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)