|
| [31] PAL | 2011-09-25 20:15:20 |
 Ha már Tesla neve említésre került, ezúttal az elektronikában jártas(!) kísérletező kedvű szakik kedvében szeretnék járni néhány nekik való, (de természetesen látványos) fizikai jelenségen alapuló kísérlettel: Ezek közül az első Tesla tekercse. (1. kép) A jelenség fizikai leírása pedig elolvasható itt!
Az igazán profik pedig megépíthetik a LIFTER-t (2. kép), ami szintén - az előbbihez hasonló módon - egy nagy feszültségű(!) tartományban működő (repülő)eszköz, egyébként ez a felvétel egy mozgó alkatrész nélküli, zajmentes, elektromos VTOL kísérleti demonstrációja, melynek működése a fizikában viszonylag "fiatal" és ritkán vizsgált jelenséggel, a Biefeld-Brown effektus -sal írható le.
(Kísérletező kedvűek FIGYELEM! Ahogy az előbbivel, úgy a Lifterrel való kísérletezés is KOMOLY SZAKÉRTELMET ÉS ÓVATOSSÁGOT igényel, mert az áramütés ÉLETVESZÉLYES!)
De a kevésbé gyakorlottak is építhetnek például ilyet, ahol szabályozható magasságú a régebbi videókon is látható elektromágneses-lebegtetés. (3.kép) (a Maglev-vasút fizikájától egyébként alapvetően eltérő működési elvű ez a kapcsolás, ráadásul ez (az előzőekhez képest) házilag is viszonylag egyszerűen kivitelezhető és megérthető:ITT!)
Aki pedig igazi látványosságot szeretne összedrótozni... annak itt van a doki kedvence, mely a közismert stroboszkóp-hatást emeli már-már művészi szintre: Emlékezzük Dr. Emmett Brown-ra, aki EZT látván biztosan a szivéhez kapna, miközben azt kiabálná: "...Felborult a tér-idő kontinuum! Te magasságos egek!" :-))
|
 |
| Előzmény: [29] lorantfy, 2011-09-09 22:51:06 |
|
|
|
| [28] lorantfy | 2011-09-05 19:03:18 |
 Nagyon jó ez a giroszkópos videó! Az egyik legérdekesebb alkalmazása a segway.
Volt szerencsém már kipróbálni, nagyon király kis jármű, bár én személy szerint szívesebben gyalogolok vagy futok, de nagy élvezet vele közlekedni.
Egy japán továbbfejlesztés, bár ennek aztán semmi értelme a közlekedést tekintve. Érdekes, hogy csak egy kereke van és mégis képes oldalazó mozgásra.
|
| Előzmény: [25] Hajba Károly, 2011-09-01 00:28:39 |
|
| [27] jonas | 2011-09-04 21:54:53 |
 Most ugyan nyár van, de téli kiránduláskor talán más is látta, hogy ha egy jégtábla teljesen a patak vize alá merül, akkor láthatatlan.
|
| Előzmény: [26] PAL, 2011-09-02 23:10:45 |
|
| [26] PAL | 2011-09-02 23:10:45 |
 A láthatlan üveg
A fenti - talán sokak által ismert - videó nekem egyszerűségénél fogva vált az egyik kedvencemmé (remélem még nem szerepelt korábban a fórumban, ha mégis, előre is elnézést kérek az ismétlésért).
Két kis fejtörőt is csatolok hozzá, elsősorban ezeket a fiatalabb tanulóknak szánom, de természetesen fizikában járatosak könnyűszerrel megválaszolhatják őket (persze kipróbálni nyilván izgalmasabb dolog), és bár eldöntendő kérdésekről van szó, azért egy "Igen.", vagy egy "Nem." mellé legalább egy-két mondatnyi magyarázatot illik fűzni.
1. Vajon tetszőleges alakú/falvastagságú üveggel kísérletezve ugyanezt az eredményt kapnánk?
2. Vajon ha az üvegfúvó hibát ejt, és kisebb/nagyobb légbuborék kerül az üveg falába, észrevesszük?
|
|
|
|
| [23] Bütyök | 2011-08-31 00:29:51 |
 Azért kérdeztem meg, nekikezdjünk vagy nem. Mert ez valóban egyetemi tananyag. Tényleg az Euler egyenleteket írják fel. A kísérleteket a mellékelt videók jól mutatják. A tojást forgásfelületként modellezve, a súlyponti tehetetlenségi főnyomatékok közül kettő egyenlő és nagyobb, mint a harmadikra vonatkozó, ami egyúttal a test egyetlen szimmetriatengelye. Dinamikai értelemben véve is szimmetriatengely, mert a hozzá tartozó tehetetlenségi ellipszoid forgás ellipszoid. Ennek a forgástengelye a dinamikai szimmetriatengely. A tojás egyetlen pontban érintkezik a kényszer felülettel (egyszerűen vegyük a síkon megpörgetett tojást). Ez a pont biztos a forgástengely pontja. Pillanatnyilag akkor dinamikai értelemben vett forgástest, ha az érintkezési ponthoz tartozó tehetetlenségi ellipszoid forgási ellipszoid. Ennek forgástengelye a pillanatnyi dinamikai szimmetriatengely. Tehát az érintkezési pontra vonatkozó tehetetlenségi tenzort kell használni. Az Euler egyenleteket is erre a pontra vonatkozóan kell felírni.
A kérdés tehát annyi, hogy a pillanatnyi dinamikai szimmetriatengely egybeeső e a pillanatnyi forgástengellyel a mozgás folyamán, vagy nem. Ha már igen, akkor kettő kérdés van.
A tanár úr példájában vett egy forgási ellipszoidot. Ennek forgástengelyre eső végeit piros és kék színnel megjelölöm. Milyen kezdeti feltételek esetén fog a piros vagy a kék végére felállni a test? Induláskor felülnézetben legyen mindig a kék a bal kéz felől.
Ugyan így megjelölöm a tojás végeit. (Talp és hegy.) A talpa mindig jobb kéz felé esik induláskor.
Persze esélye sincs a tojásnak nem a hegyére felállni, ha a hegyében gömbcsuklóval megfogatjuk és állványhoz kötjük. És megpörgetjük.
Az eredeti kísérletben persze a tojás szabad mozgást végez. Az a kérdés,hogy megpörgethető e a tojás úgy, hogy a hegyére álljon fel? Erre még ugyan példát nem láttunk.
De a legutolsó videón a csapos gömbsüveg mutatja, hogy van ilyen.
Több videó van és általában ilyen hegyben végződő érintkezési pont felé keskenyedő forgástestet használnak, tehát inkább a hegyén pörgő tojás a kedveltebb forma.
Ez a probléma térbeli vektorszámítási gyakorlatként és az abból a fizikai mondanivaló kiolvasásának módja szempontjából talán nem túlzás itt.
Tehát az előző rajz szerinti K vektor az függőleges, az érintkezési pontból a súlypontba mutató vektor térbeli, és a szögsebesség vektorról is csak annyi bizonyos, hogy térbeli vektor egyelőre, de hatásvonalát meg kell határozni.
Az Euler egyenlet a perdületet használja. Ez az impulzusvektor nyomatéka a pillanatnyi forgáspontra. Ez időben változó nagyságú és irányú (térbeli) vektor a mozgás folyamán. Kezdőpontja ismert, az érintkezési pont.
Továbbá a test súlypontjának gyorsulása miatt van még egy erő Newton II. szerint F=ma. Ez is egy térbeli vektor, aminek kezdőpontja a súlypont. A súlypont gyorsulásvektora pedig a szögsebesség és a szöggyorsulás vektorból számítható. Végül az érintkezési pontra számított nyomatékvektor az kifejezhető az érintkezési pontban számolt tehetetlenségi nyomaték tenzor és a szöggyorsulásvektor illetve szögsebesség vektorral.
Amennyiben igaz a mozgásra, hogy minden pillanatban a nyomaték vektor egyenlő a perdület derivált vektorral ugyanarra a pontra számolva (tehát vagy az van, hogy az a pont amire felírom nyugvó pont, vagy a súlypont sebesség vektora párhuzamos a pont sebességvektorával), akkor írhatók fel az Euler egyenletek, arra a pontra vonatkoztatva.
Végül Alexander mondott még sokféle modellt. Ebből szögsebesség nagyságára és az energiára tett megfontolások a tárgyhoz tartoznak. Mert az állandó perdülethez tartozó felületek is forgási ellipszoidon lehetnek. Végül pedig az állandó mozgási energia nívófelületei is lehetnek forgási ellipszoidon. A szögsebesség növelésével a mozgási energia nő. Végül pedig ezeken az ellipszoidokon természetesen mindig egy felületi pontba mutató vektor a tényleges szögsebesség vektor. Ezen az ellipszoidok középpontja a pillanatnyi érintkezési pont. A kettő felület között a kapcsolat az invariábilis sík. Most ez párhuzamos azzal a síkkal amin a tojás mozog. Ezen gördül az ellipszoid, úgy hogy középpontja a pillanatnyi forgáspont, a síkon leírt görbe és az ellipszoidon leírt görbe pontjait a szögsebesség vektor, mint hely vektor rendeli össze. A mozgási energia arányos tehát a síktól vett távolságával az invariábilis síknak.
|
|
|
| [21] lorantfy | 2011-08-30 18:50:55 |
 Szerintem is kár rögtön ágyúval lőni a kisegérre. (Elég lesz akkor, ha majd elefánttá dagad). Igyekezzünk egyszerűsíteni a problémát, amennyire ez lehetséges anélkül, hogy elveszne a lényeg.
A homogén forgási ellipszoid közelítés szerintem megfelelő. A kísérlet remélhetőleg egy szabályos műanyag forgási ellipszoiddal is hasonlóan játszódna le. (Azért ki kéne próbálni!) Ennek két stabil forgási állapota van. Most már csak azt kell megmagyarázni miért tér át a kistengely körüli forgásról a nagytengely körülire, ha egy bizonyos fordulatszámnál gyorsabban pörgetjük meg a kistengelye körül.
Az Euler-egyenlet is az energia megmaradást fogalmazza meg, csak teljesen általánosan. Mi lenne, ha itt csak a tojás helyzeti és forgási energiáját figyelnénk. A levegő és az asztallal való súrlódás fékező hatásától eltekinthetünk.
A tojásra a súrlódási erőn kívül két külső erő hat: a gravitációs erő és az asztal nyomóereje. A gravitációs erőt képzelhetjük a tömegközéppontba, ami itt a geometriai középpont. Az asztal nyomóereje pedig az érintkezési pontban hat. Ezek az erők függőleges irányúak, a mozgás kezdő (kistengely körüli forgás) és végállapotában (nagytengely körüli forgás) során nincs forgatónyomatékuk.
A felágaskodáskor ez a két erő erőpárként működik egy vízszintes forgástengelyre nézve és ekkor figyelembe kell még vennünk a súrlódási erő forgatónyomatékát is.
A függőleges tengelyre nézve ezeknek az erőknek nincs forgatónyomatéka, így erre a tengelyre vonatkozó perdület megmarad.
Felágaskodáskor a tömegközéppont magasabbra kerül, így a megforgatáskor kapott forgási energia egy része helyzeti energiává alakul.
A forgási ellipszoid tehetetlenségi nyomatéka a nagytengelyre nézve kisebb mint a kistengelyre.
|
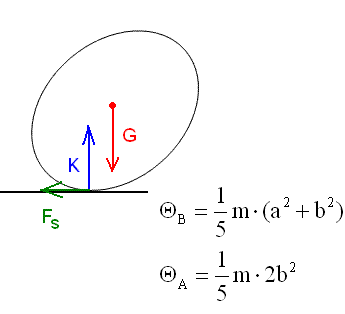 |
| Előzmény: [20] Alekszandrov, 2011-08-29 23:20:01 |
|
| [20] Alekszandrov | 2011-08-29 23:20:01 |
 A következőképpen látom a jelenség magyarázatát! Gyakorlatilag közelítsünk a problémához. A gőzmozdonyok rudazattal kapcsolt hajtott kerékpárjait hozom példaként! Figyeljétek meg, hogy a rudazat rögzítési pontjával átellenesen kis fémnehezék van beépítve a kerékbe azért, hogy az óriási tömegű kerék forgását kiegyensúlyozzák. A rudazat egyenetlen tömegeloszlást jelent a (különben) szimmetrikus mozdonykerékben. Ha nem lenne ez az ellen-tömeg, akkor a kerék gyors forgásakor olyan erő terhelné a tengelyeket, ami azok törését is előidézheti! (Elméletileg ez felel meg annak, hogy a tehetetlenségi tenzor nem diagonális, azaz eltérítő nyomatékok lépnek fel)A cél pontosan az, hogy ezeket az eltérítő (deviációs) nyomatékokat megszüntessük! Mármost kérdezheti valaki: hogy kerül a mozdonykerék a tojásos asztalra? :-) Indokom a következő! Alapvetően egy test kétféle módon hozható forgásba: 1. átdöfik egy valóságos tengellyel, amit a két végén rögzítenek, és máris foroghat a test. Természetesen általában a forgó test ráncigálja a tengelyt, így az igénybevételt jelent a rögzítési pontokban. Most képzeletben kezdjük el lassan változtatni a tengely térbeli irányát (esetleg helyzetét is kell)! Előfordulhat olyan állapot, amikor a rögzítési pontok semmilyen ráncigálást nem "éreznek", tehát a rögzítéseket akár meg is szüntethetjük, sőt a tengelyre sincs ilyenkor szükség. Ezt a speciális esetet nevezzük szabad tengely körüli forgásnak (ekkor a tehetetlenségi tenzor diagonális, azaz a deviációs nyomatékok eltűnnek). A térben ezek a tengelyirányok általában véges számúak (eltekintve a „túl nagy” szimmetriától pl. a gömb esetén), hiszen homogén tömegeloszlást feltételezve csakis a tömegközépponton átmenő és valamiféle szimmetriával rendelkező tengelyek esetén kapunk ráncigálás mentes forgást. Ezeket a térbeli tengelyeket nevezzük fő tehetetlenségi tengelyeknek. Ami itt a döntő, hogy a test szabad tengely körüli forgási állapotai irány kvantáltak, azaz csak véges számú különböző nagyságú tehetetlenségi nyomaték jöhet szóba. A főtt tojást homogén forgási ellipszoidnak tekintve valóban két lényegesen különböző fő tehetetlenségi nyomaték van: az egyik a kistengelyre vonatkozó, a másik pedig a nagytengelyre vonatkozó tehetetlenségi nyomaték. Mindkettő körül stabil forgás alakulhat ki, ha a megfelelő szögsebességű forgásba hozzuk! Tessék kipróbálni, a főtt tojás gyönyörűen forog a kistengelye körül is, csak nem szabad túl gyors forgásba hozni (vagy másként mondva bizonyos nagyságú munkánál nagyobbat végezni a forgásba hozatalkor). Amennyiben ennél a jól meghatározott "energia intervallumnál" szélesebb sávot adunk a főtt tojásnak, akkor ezt az energiát csak egy másik (nagytengely körüli) forgási állapotban képes hordozni! Nagyjából így értelmezem ezt a jelenséget a józan paraszti eszemmel. :-) Szép éjcakát Mindenkinek!
|
| Előzmény: [17] Alma, 2011-08-29 21:13:18 |
|
| [19] lorantfy | 2011-08-29 21:26:17 |
 Állítsd meg a videót 40 sec előtt és próbálj magyarázatot találni a golyó viselkedésére! Magic Ball
|
|
| [18] Alma | 2011-08-29 21:16:09 |
 Illetve egész pontosan azt láttam be ezzel, hogy ha van időben nem (csak nagyon lassan) változó megoldás, az csak úgy lehetséges, ha a hossztengely körül forog. A nehézségi erő nyomatéka pedig akkor tud eltűnni, ha a forgástengely függőleges. Ezért áll fel a tojás.
|
| Előzmény: [17] Alma, 2011-08-29 21:13:18 |
|
| [17] Alma | 2011-08-29 21:13:18 |
 Szia!
Ez egy egyetemen mechanikából részletesen tárgyalt probléma, ha érdekel mélyebben a matematikája, akkor a helyedben megnéznék egy egyetemi mechanika könyvet (pl Nagy Károlyét).
Ha a koordináta-rendszered tengelyeit a tehetetlenségi főtengelyek irányában veszed fel, akkor a tehetetlenségi nyomaték tenzor diagonális lesz, és ekkor lehet alkalmazni az Euler-egyenletet.
Wikipedia: Euler equations (rigid body dynamics)
Esetünkben a tojás két fő tehetetlenségi nyomatéka közel megegyezik, a harmadik pedig eltér, mégpedig kisebb az előző kettőnél. Ezt behelyettesítve az Euler-egyenletbe keressük a probléma egyensúlyi megoldását, amikor az időderiváltak eltűnnek. Ha a forgatónyomatékokat zérusnak vesszük (reális feltételezés), be lehet látni, hogy vagy a megkülönböztetett tengely iránya körüli szögsebességnek kell zérusnak lennie, vagy mindkettő másiknak. Be lehet látni (kicsit megperturbálva a rendszert), hogy csak az utóbbi eset stabil. Ez pedig az az eset, amikor a tojás feláll a talpára.
Remélem valamennyire érthető ez a vázlatos magyarázat. Amiket írtam nagyjából le is ellenőriztem, nem csak tippeltem, de nem vizsgáltam túl részletesen a problémát őszintén szólva.
|
| Előzmény: [16] Bütyök, 2011-08-29 15:28:31 |
|
| [16] Bütyök | 2011-08-29 15:28:31 |
 Akkor a kísérleteket elvégezték. És publikálták is:-) Megmaradt az elméleti munka ezzel. Gondolom barátságban vagyunk a "képletekkel", csak az a kérdés van e türelem. (A kömalban egy elhanyagoltabbnak látszik a fizika. Belevágjunk a megoldásba?
|
|
|
|
|
| [12] Bütyök | 2011-08-28 12:38:53 |
 "Megkérdezném,mert tudatlan és lusta vagyok,ahhoz hogy képletekből rájöhessek,és a topik címe is bíztat; miért áll fel a főttojás,a tompábbik végére,ha elfektetve megpörgeted? (akit zavar a kérdés,attól elnézést kérek,tudom hogy nem áll meg az élet,ha nem tudom meg a választ :) )"
?
|
|
| [11] lorantfy | 2011-08-26 23:40:07 |
 Emlékszem gyerekkoromban mikor a slagot lóbáltam észrevettem, hogy furcsán lengedez. Akkor nem tudtam miért és azóta sem jutott eszembe, hogy ez milyen jó lehetőség a Coriolis-erő bemutatására, míg meg nem láttam ezt a csöves kísérletet. Hogy ezt felhasználva áramlás mérő műszert lehet készíteni ez tényleg nagy ötlet!
|
| Előzmény: [10] SmallPotato, 2011-08-26 11:02:18 |
|
| [10] SmallPotato | 2011-08-26 11:02:18 |
 A csuda gondolta volna, hogy ezt a Coriolis-eredetű csődeformációt még mérésre is fel lehet használni (mármint hogy a zavaró tényezőket hatékonyan le lehet választani)! Számomra nagyon tanulságos volt.
|
| Előzmény: [9] lorantfy, 2011-08-25 20:58:43 |
|
|
|
