| [19] PAL | 2022-01-20 01:24:41 |
 Készítettem a közepes diákok számára egy hasznos ábrát, melyről néhány nevezetes szög trigonometrikus függvényének pontos értéke azonnal kiolvasható. (Ez persze itt-ott fellelhető a neten, de gondoltam azért itt is legyen meg, hátha valaki itt keresné.) Az egységsugarú körben jól elhelyezetett négyzet és szabályos háromszög megfelelő oldalainak megválasztásával és néhány Pitagorasz-tétel felírásával - remélem - minden magáért beszél, a színek pedig szavak nélkül mutatják mi-hol szerepel a képletekben (a különböző színű, de azonos változók nyilván azonos értékűek). Később - reményeim szerint - ebbe az ábrába a megfelelő helyre berajzolt szabályos ötszöggel is megpróbálom kiegészíteni, és akkor a 18°-72°-os szögekre vonatkozó szögfüggvények értékei is leolvashatók lesznek. Ha hibát találtok az ábrában, kérem itt a fórumon jelezzétek, és javítom, amint tudom, köszönöm. Addig is, mindenki felhasználhatja bárhol, aki ellenőrizte, hogy rendben van! :-) Az ábra ide kattintva érhető el a nevezetes szögekkel.
|
|
|
| [17] w | 2013-02-05 16:35:54 |
 Én kissé más Batman-görbét ismerek, ami órán is előkerült: f(x)=|p(x)| grafikonja az alvó Batmant ábrázoló görbe, ahol p másodfokú polinom D>0-val. Egy x tengelyre való tükrözéssel meg éber Batman adódik :-)
|
| Előzmény: [16] PAL, 2013-02-03 21:49:28 |
|
| [16] PAL | 2013-02-03 21:49:28 |
 Kis vasárnap esti humor, hátha van, aki nem látta még:
Íme egy Batman-görbe :-)
Batman curve
|
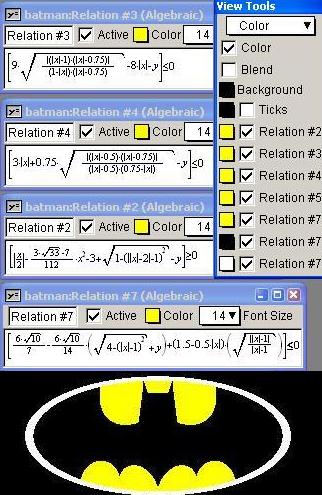 |
|
|
|
| [13] lorantfy | 2012-01-26 16:32:41 |
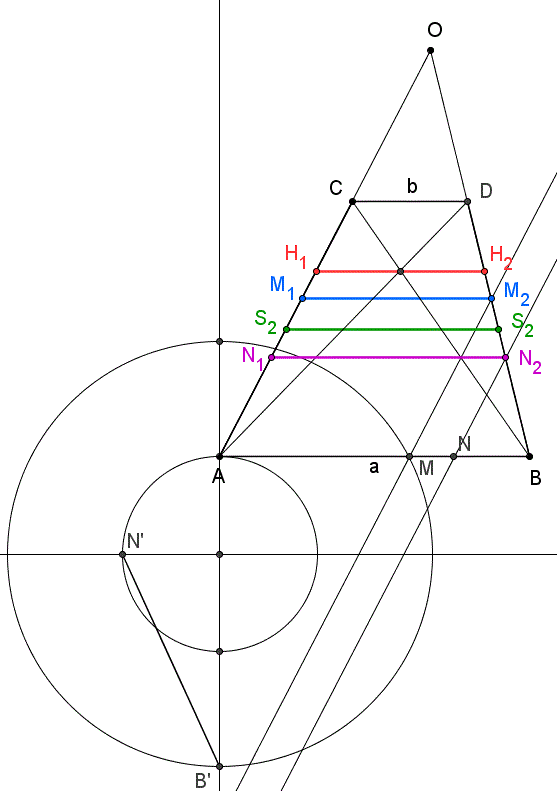
 Megcsináltam végre a KÖZEPEK A TRAPÉZBAN ábrát szerkesztéssel. Felülről lefelé a jelöléseknek megfelelően az a és b oldal harmonikus, mértani, számtani és négyzetes közepének megfelelő szakaszok láthatók.
|
 |
| Előzmény: [9] sakkmath, 2012-01-24 20:46:28 |
|
|
| [11] lorantfy | 2012-01-24 23:13:29 |
 Nem volt még időm rá, hogy rendesen megszerkesszem. Az alap ábrát egy szakdolgozatból másoltam ki. A a megjegyzéseket színessel én írtam rá. Végül is itt most annyira nem lényeges, hogy a vonalak hajszál pontosan jó helyen vannak-e, hanem csak annyi, hogy ezek a közepek a trapézban milyen tulajdonsággal rendelkeznek. Nyilván szebb lesz helyesen szerkesztve, hamarosan felteszem.
|
| Előzmény: [9] sakkmath, 2012-01-24 20:46:28 |
|
|
| [9] sakkmath | 2012-01-24 20:46:28 |
 Nekem is tetszik, a trapézos szintén.
Utóbbihoz két kérdés:
Várható-e korrekció Jonas fölvetésére válaszul?
Ha szakkönyvből, vagy a világhálóról származik, létezik-e idegennyelvű változata? Elsősorban angolra, vagy franciára gondolok.
|
| Előzmény: [4] lorantfy, 2011-09-22 16:01:07 |
|
| [8] sakkmath | 2012-01-21 18:42:39 |
 Bernar Venet képzőművész szeret matematikai, fizikai, statisztikai témájú egyenleteket festeni. (Úgy tudom, a művész egyik szakterületnek sem művelője. Venet honlapja itt található.)
Beszúrom az egyik egyenletes képét, megtoldva három (találós) kérdéssel:
1) Mi az egyenlet témája és neve?
2) Az egyenlet neve két változatban is ismert. Melyik a helyes?
3) Alakilag rendben van-e az ábrázolt egyenlet?
|
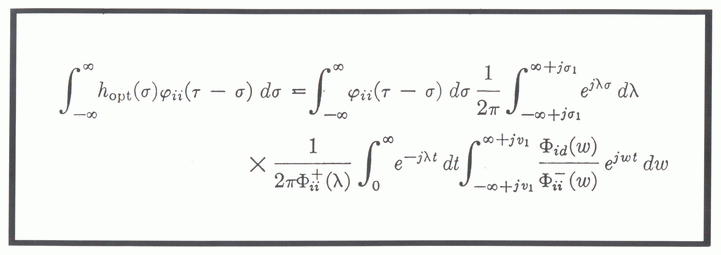 |
|
|
|
|
| [4] lorantfy | 2011-09-22 16:01:07 |
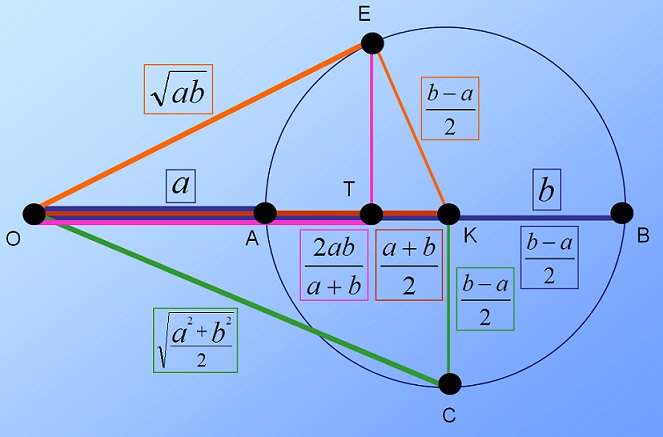
 Jó a kezdeményezés! Bár nem animáció, de a matematikai közepek egyik geometriai szemléltetése, ami nekem tetszik, ezért fölteszem, hátha másnak is hasznos lehet.
|
 |
|
|
|
| [1] PAL | 2011-09-18 23:04:33 |
 Lorantfy mintájára szeretnék indítani egy témát, mely nem a fizikai kísérleteket, látványosságokat mutatja be, hanem a MATEMATIKA világába kalauzol el, elsősorban érdekes képsorok, ANIMÁCIÓK vagy videók formájában.
Továbbá természetesen én is örömmel látok ilyen jellegű mozgóképeket ebben a témában, és remélem az általam feltöltöttek között pedig akad olyan, amit ti is szivesen néztek végig.
(Sajnos a link-ek kivétel nélkül angol nyelvűek, és bár terveim között szerepel, ezen külföldi videók szakszerű magyar nyelvű fordítása és feliratozása, erre ezidáig sajnos nem jutott időm...)
|
|
