| [1123] Berko Erzsebet | 2021-08-07 08:21:41 |
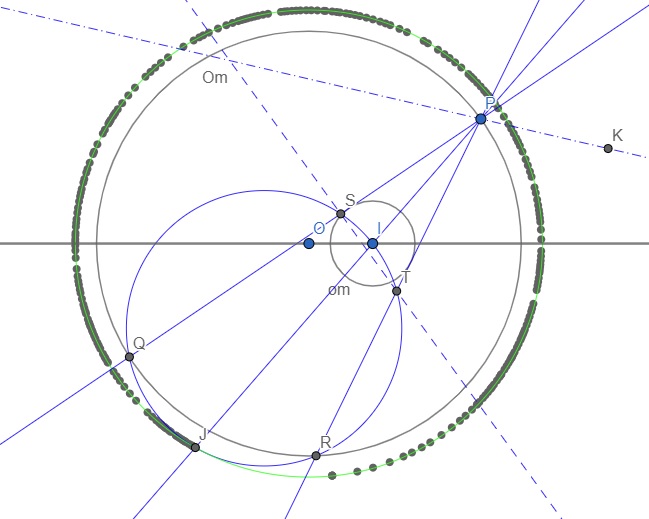
 Van 6 pontunk egy körön. A szelőtétel miatt PS*PQ=PT*PR=PI*PJ=PI*(PM+MK), ahol ST metszet PJ=M. Lehet, hogy ez a tétel adta azt a gondolatot, hogy körérintők helyett metsző egyenesekkel foglalkozzak, ilyenkor persze már nincsenek kúpszeletek, de az a bizonyos egyenesek mintha mindig ugyanazon a ponton mennének át. Amikor a körközéppont (kis körnél) helyett egy körközéppont melletti ponttal foglalkoztam, akkor már ez nem igaz, vagyis annak szerepe van.
|
|
| [1122] Berko Erzsebet | 2021-08-06 11:10:40 |
 Vagy esetleg más középponttal. A körközéppontok elhelyezkedésétől, sugarak arányától... függően én többféle kúpszeletet el tudok képzelni. Kör, ellipszis, hiperbola... Kúpszeletek szerkesztése két fixkörrel, kétkörös szerkesztések, illetve még csak elmélkedések...
|
| Előzmény: [1121] HoA, 2021-08-06 08:26:38 |
|
|
| [1120] Berko Erzsebet | 2021-08-06 07:05:26 |
 A J pont mintha kúpszeleten mozogna. Tehát a J pont, nem a K.
|
|
| [1119] HoA | 2021-08-05 00:00:59 |
 A sejtés ( "A két kör középpontját összekötő egyenesen van" ) könnyen bizonyítható. Vegyünk fel Ω -n egy P1 és egy P2 pontot, melyek szimmetrikusak Ω és ω centrálisára. A feladatban leírt alakzatokat P1 -hez illetve P2 -höz megrajzolva, azok egymás tükörképei lesznek a centrálisra, így a P1K1 és P2K2 egyenesek is. Ha tehát van a feladat állításának megfelelő pont, melyen minden PK egyenes áthalad, az csak P1K1 és P2K2 metszéspontja lehet. Ez pedig - ha létezik - a szimmetria miatt a centrálison van.
( A hozzászólásodban leírt metszéspont I -nek Ω -ra vonatkozó inverze. )
|
| Előzmény: [1115] Berko Erzsebet, 2021-08-02 17:02:33 |
|
|
| [1117] Berko Erzsebet | 2021-08-03 18:49:44 |
 Szerintem a K pont többféle görbén mozoghat. (Nézzük azt az esetet, amikor a két kör nem koncentrikus. Mivel sérül a szimmetria, ezért nem tudom elképzelni, hogy kijöhet ellipszis. Inkább egy igazi tojás:) Persze, mivel ezek csak elmélkedések, akár ellipszis is kijöhet. A keresett pont I-hez van közelebb a két középpont közül.)
|
| Előzmény: [1116] Lpont, 2021-08-03 15:54:01 |
|
| [1116] Lpont | 2021-08-03 15:54:01 |
 Helyes a sejtésed, bár az én ábrámon a keresett pont nagyon messze van I-től. Nyilván a két kör helyzete és sugarainak nagysága meghatározó.
Nem tudom, hogy közelebb visz-e a megoldáshoz a tény, miszerint K pont egy ellipszisen mozog és az általad említett nagy kört érintő egyenesek érintik ezt az ellipszist is.
|
| Előzmény: [1115] Berko Erzsebet, 2021-08-02 17:02:33 |
|
| [1115] Berko Erzsebet | 2021-08-02 17:02:33 |
 A.779. Ha a két kör koncentrikus, akkor néztem olyan esetet, amikor nincs második metszéspont (pl. 1, illetve 2 egység sugarú kör). Néztem olyat is, amikor az I pont képe tengelyes tükrözés után megegyezik az eredeti ponttal: 1, illetve 3 egység sugarú kör. Most legyen a két kör nem koncentrikus. Hol van az a pont, amin átmennek az egyenesek? Csak sejtés. A két kör középpontját összekötő egyenesen van. (I ponthoz közel, szereti I pont társaságát:) Kössük össze a két középpontot, majd állítsunk merőlegest I-ben erre az egyenesre. Metszeni fogja a nagyobb sugarú kört. Ebben a pontban tekintsük az érintőt. Az érintő fogja kimetszeni a pontot a két kör középpontját összekötő egyenesből.
|
| Előzmény: [1114] sakkmath, 2021-07-19 22:51:45 |
|
| [1114] sakkmath | 2021-07-19 22:51:45 |
 A szerkesztőség nem közölte a 2020. \displaystyle májusi \displaystyle számban kitűzött A. 779. feladat megoldását. Talán felfrissítené a Fórumot, ha valaki feltenné a sajátját.
A. 779. Adott két rögzített kör, \displaystyle \Omega és a belsejében \displaystyle \omega. Az \displaystyle \omega középpontja \displaystyle I. Az \displaystyle \Omega körön mozog egy \displaystyle P pont. A \displaystyle P-ből \displaystyle \omega-hoz húzott érintők második metszéspontja \displaystyle \Omega-val \displaystyle Q, illetve \displaystyle R. Az \displaystyle IQR kör második metszéspontjai a \displaystyle PI, \displaystyle PQ és \displaystyle PR egyenesekkel rendre \displaystyle J, \displaystyle S, illetve \displaystyle T. A \displaystyle J tükörképe az \displaystyle ST egyenesre \displaystyle K. Mutassuk meg, hogy a különböző \displaystyle PK egyenesek egy ponton mennek át.
(7 pont)
|
|
| [1113] Róbert Gida | 2021-06-08 23:38:17 |
 "Van-e valakinek olyan megoldása, amely a hivatalostól eltérő módszert alkalmaz?"
Egy old school megoldás. Legyen a konstans tag: \displaystyle u=\frac{71+17\sqrt{17}}{2}.
Feltehetjük, hogy \displaystyle a,b,c\ge 0. Rögzített \displaystyle b^4+c^4 esetén mikor lesz legszorosabb az egyenlőtlenség? Könnyű, ekkor a bal oldal fix, míg a jobb oldalra: \displaystyle 2(bc)^2\le b^4+c^4 és \displaystyle (b^2+c^2)^2\le 2(b^4+c^4)-ből látható, hogy az egyenlőtlenség jobboldalának: \displaystyle 4abc+a^2(b^2+c^2)+3b^2c^2 minden tagja akkor a legnagyobb, ha \displaystyle b=c, és ez el is érhető: \displaystyle b=c=(\frac H2)^{1/4} választással, ahol \displaystyle H=b^4+c^4 .
Továbbiakban így feltehető \displaystyle c=b ezzel kell: \displaystyle 2a^4+4b^4+u\ge 4ab^2+2a^2b^2+3b^4 rendezve kell: \displaystyle b^4-(4a+2a^2)b^2+(2a^4+u)\ge 0, teljes négyzetté alakítva: \displaystyle G(a,b)=(b^2-(2a+a^2))^2+(a^4-4a^3-4a^2+u)\ge 0 kell. Legyen \displaystyle F(a)=a^4-4a^3-4a^2+u, ekkor \displaystyle F'(a)=4a^3-12a^2-8a ennek zérushelyei: \displaystyle a1=0, a23=\frac{3\pm \sqrt {17}}{2}, itt \displaystyle a2<0=a1<a3. Mivel \displaystyle a\ge 0-t kell csak vizsgálnunk: az \displaystyle F fv. szig. monoton csökken \displaystyle [0,a3] intervallumon, majd \displaystyle [a3,\infty)-n növekszik, ezért \displaystyle [0,\infty)-n a minimum \displaystyle a=a3-n van, de ott éppen kis számolással \displaystyle F(a)=0 is teljesül, ebből triviálisan \displaystyle G(a,b)\ge 0 ami kellett. És egyenlőség pontosan akkor teljesül [bár ezt a feladat nem kérdezte], ha \displaystyle a=\frac{3+\sqrt{17}}{2}, b=c=\sqrt{a^2+2a}. Általában pedig páros soknak [esetünkben pontosan 2-nek] az előjelét megváltoztatva kapunk még egyenlőséget.
|
| Előzmény: [1112] sakkmath, 2021-06-08 16:30:53 |
|
| [1112] sakkmath | 2021-06-08 16:30:53 |
 Még valami, ismét a \displaystyle MAPLE (és a hivatalos megoldás) segítségével.
Az egyenlőtlenségben egyenlőség teljesül ezekre az (a, b, c) számhármasokra:
\displaystyle (p, q, q); (p, -q, -q); (-p, q, -q); (-p, -q, q).
Látható, hogy e számhármasokon belül páratlan sok számnak pozitív az előjele.
Van-e valakinek olyan megoldása, amely a hivatalostól eltérő módszert alkalmaz?
|
| Előzmény: [1111] sakkmath, 2021-06-08 12:19:18 |
|
|
| [1110] sakkmath | 2021-06-07 23:45:34 |
 Elírást fedeztem fel a B.4784. feladat (2016. március!!) hivatalos megoldásában.
A honlapon a megoldás befejezése: (…) és \displaystyle a, b, c számok közül páros soknak pozitív az előjele. (1)
Úgy látom, ez hibás, és (1) helyére ezt kell írni:
(…) és az \displaystyle a, b, c számok közül páratlan soknak pozitív az előjele;
vagy ezt:
(…) és az \displaystyle a, b, c számok közül páros soknak negatív az előjele.
A fentiek a Maple programmal igazolhatók. Az alábbi kép beszúrásával cáfolom (1)-et.
A kép szerinti esetben \displaystyle a > 0, c > 0 és \displaystyle b < 0, azaz: két számnak (páros soknak) pozitív az előjele. Mint látható, a Maple (2019) szerint a nullára redulált egyenlet helyettesítési értéke \displaystyle 284 + 68\sqrt{17}, ami nem zérus! A további három eset cáfolatát mellőzöm.
Remélem, a nyomtatott KöMaL-ban a helyes szöveg szerepel…
|
 |
|
| [1109] Róbert Gida | 2021-04-17 15:30:33 |
 A lejárt B5141 megoldása, tisztán kombinatorikus úton, sokkal egyszerűbben, mint a közöltek:
\displaystyle S=\sum_{i=0}^n\sum_{j=i}^n \binom{n}{i}\binom{n+1}{j+1}=\sum_{i=0}^n\sum_{j=i}^n\binom{n}{i}\binom{n+1}{n-j}=\sum_{i=0}^n\sum_{k=0}^{n-i}\binom{n}{i}\binom{n+1}{k}
Tegyünk le egy sorba \displaystyle n+(n+1)=2n+1 korongot, ezek közül válasszunk ki legfeljebb \displaystyle n-et. Ezt nyilván \displaystyle S féleképpen tehetjük meg: az első \displaystyle n-ből \displaystyle i-t, míg az \displaystyle n+1-ből \displaystyle k\le{n-i} darabot választhatunk. De trivi szimmetria mutatja, hogy ezt az összes eset felében tehetjük meg [másik felében több, mint \displaystyle n-et választanánk], azaz \displaystyle S=\frac{2^{2n+1}}{2}=2^{2n}, ami kellett.
|
|
| [1108] Gömb | 2021-03-24 20:01:36 |
 Igen, igazad van! Köszönöm szépen a válaszod.
Ez olyan logikus megoldás, kár hogy nekem nem jutott eszembe :'D
Egyébként akkor azt kellett volna megsejtenem, hogy \displaystyle n_1, \displaystyle n_2 és \displaystyle n között valami exponenciális kapcsolat van... Mindegy, mert még így is elég messze lettem volna az igazi (rész)megoldástól.
A tanulság számomra: az új megközelítés(ek) nagyon fontos(ak).
|
|
| [1107] Erben Péter | 2021-03-24 12:28:11 |
 Ha elfogadod a hivatalos megoldásban leírt formulát helyes megoldásnak, vagyis hogy
\displaystyle f(n)=\frac{(2+\sqrt{3})^n+(2-\sqrt{3})^n}{2},
akkor csak az a kérdés, hogy adhat-e a te megközelítésed egy másik alakot ugyanerre a függvényre.
Mivel \displaystyle x_1 és \displaystyle x_2 konstans, \displaystyle n_1\cdot x_2 - n_2\cdot x_1 egy legfeljebb másodfokú polinom, ha \displaystyle n_1-ről és \displaystyle n_2-ről felteszed, hogy másodfokú polinomok.
Látható, hogy \displaystyle f(n)>\frac{3^n}{2}. Ez pedig elég nagy \displaystyle n esetén \displaystyle n bármilyen másodfokú kifejezésénél nagyobb lesz. Ezen utolsó állítás bizonyításához elég azt látni, hogy amikor \displaystyle n 1-gyel nő, akkor az \displaystyle f(n)-re adott alsó korlát háromszorozódik, míg nagy \displaystyle n-ek esetén egy másodfokú \displaystyle g-re \displaystyle g(n+1) és \displaystyle g(n) aránya közel esik 1-hez.
|
| Előzmény: [1106] Gömb, 2021-03-24 07:34:13 |
|
| [1106] Gömb | 2021-03-24 07:34:13 |
 Köszöntök Mindenkit!
Szóóóval, hogy is kezdjem... Egy feladat elgondolkodtatott, bár már megnéztem a megoldását, és még úgy is.
A feladat: B.5109.
Úgy kezdtem neki, hogy utánanéztem neten a négyzetszámoknak, így azokból ki tudtam indulni, az ötlet az volt, hogy mivel a négyzetszámokra van egy explicit képlet, ezért ennél a sorozatnál megpróbálkozom annak a felírásával, aztán utána több tervem is volt, mit csinálok vele... Először meg akartam úgymond sejteni, aztán pl. teljes indukcióval bizonyítani. Igen ám... de itt ütköztem gondba... Ez nem is olyan egyszerű, mint hittem.
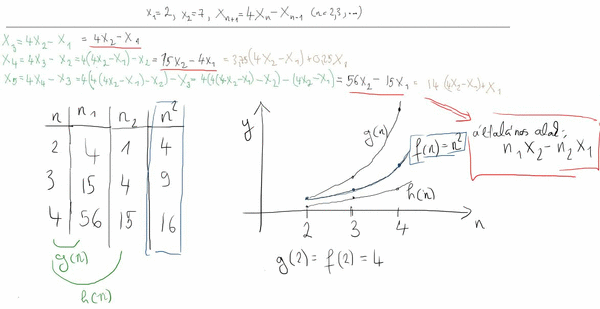
A mellékelt ábrán látszik mit akartam csinálni, de azért kifejtem: 1.) Felírtam a sorozat első 3 elemét az első két megadott tag függvényében 2.) Észrevettem, hogy: konstans*x2-konstans2*x1, (azaz \displaystyle n_1*x_2-n_2*x_1), tehát ebből kreáltam egy "általános alak"-ot. 3.) Sejtésem szerint ebben az alakban az \displaystyle n_1 és \displaystyle n_2 konstans valamilyen másodfokú függvény szerint függ össze az n-nel... 4.) Ha ezt megtudnám mondani, akkor úgymond "kész is lenne" az explicit formula, mivel mindent \displaystyle x_1;\displaystyle x_2 (= ami két konkrét szám) és n-nel kifejeztem... De már a 3. pontnál elakadtam, ötletek?
Egyáltalán van a feladatnak ezzel a "módszerrel" megoldása?
|
 |
|
| [1105] HoA | 2019-10-28 14:20:13 |
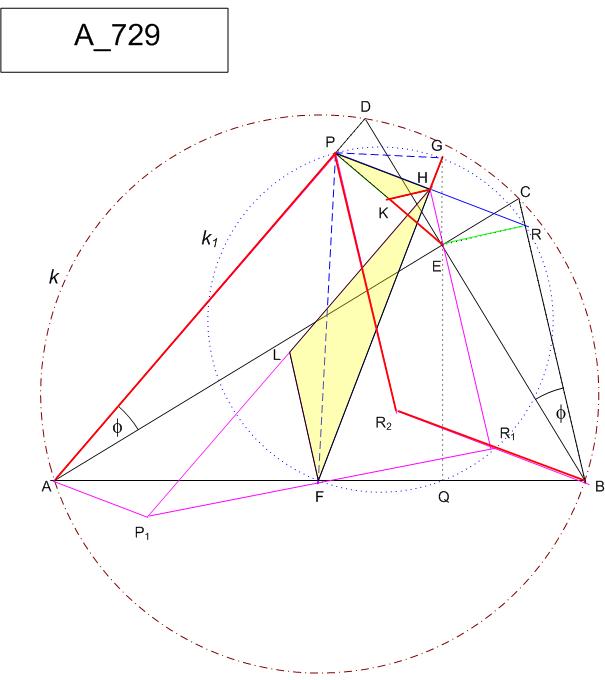
 Az \displaystyle \bf{A. 729.} feladatra [1104] -ben adott megoldás egyszerű, de talán nem elég szemléletes. Azzá tehető, ha az ott szereplő vektorok összetevőinek megfelelő szakaszokat beillesztjük a feladat ábrájába. Ezzel elemi geometriai bizonyítást adunk a feladat állítására. A leírásban sok lesz az ismétlés, de inkább leírom, a feladat szövegével együtt, hogy önmagában is olvasható legyen.
\displaystyle \bf{A. 729.} Az ABCD húrnégyszög átlóinak metszéspontja E, az AB oldal felezőpontja F, és az E pont merőleges vetületei a DA, AB és BC egyeneseken rendre P, Q, illetve R. Igazoljuk, hogy a P, Q, R és F pontok egy körre illeszkednek.
\displaystyle APE és \displaystyle BRE derékszögű háromszögek hasonlók, mert \displaystyle A-nál ill. \displaystyle B-nél lévő szögük a k körülírt kör \displaystyle CD ívéhez tartozó kerületi szög - jelöljük \displaystyle \phi-vel. Legyen \displaystyle BR / RE = AP / PE = ctg \phi = \lambda. A \displaystyle PR szakasz felezőpontja legyen \displaystyle H. \displaystyle P tükörképe \displaystyle AH felezőpontjára \displaystyle {P_1}, \displaystyle R tükörképe \displaystyle BH felezőpontjára \displaystyle {R_1}. \displaystyle A{P_1}HP és \displaystyle BRH{R_1} paralelogrammák, \displaystyle H{P_1} = PA = \lambda \cdot PE ; \displaystyle H{R_1} = RB = \lambda \cdot RE ; \displaystyle A{P_1} \# PH \# HR \# {R_1}B . \displaystyle A{P_1} B{R_1} is paralelogramma, átlóinak metszéspontja, az \displaystyle AB szakasz \displaystyle F felezőpontja \displaystyle {P_1} {R_1} -et is felezi. A \displaystyle {P_1} {R_1} H háromszög \displaystyle {R_1}H -val párhuzamos középvonala \displaystyle FL
\displaystyle FL = ½ {R_1} H = ½ BR = \lambda/2 \cdot RE \displaystyle HL = ½ H{P_1} = ½ PA = \lambda/2 \cdot PE.
Az \displaystyle ERP háromszög \displaystyle ER-rel párhuzamos középvonala legyen \displaystyle HK. \displaystyle HKP és \displaystyle FLH háromszögek hasonlóak, mert \displaystyle HL = \lambda/2 \cdot PE = \lambda \cdot PK és \displaystyle HL merőleges \displaystyle PK-ra; \displaystyle FL = \lambda/2 \cdot RE = \lambda \cdot HK és \displaystyle FL merőleges \displaystyle HK-ra. \displaystyle FLH és \displaystyle HKP szögek egyenlőek mint nem egymás szögtartományába eső merőleges szárú szögek. A két háromszög megegyezik két oldal arányában és a közbezárt szögben.
Így \displaystyle HF is merőleges \displaystyle PH-ra és \displaystyle HF =\lambda \cdot PH. \displaystyle HF a \displaystyle PR felező merőlegese.
Messe az \displaystyle FH egyenes a \displaystyle PFR pontokon áthaladó \displaystyle \it {k_1} kört másodszor \displaystyle G-ben. \displaystyle FG mint húrfelező merőleges \displaystyle \it {k_1} -ben átmérő. \displaystyle \it {k_1} tehát \displaystyle FG Thalész-köre. \displaystyle FPG háromszög derékszögű, \displaystyle PH az átfogóhoz tartozó magasság. \displaystyle HF / HP = HP / HG = \lambda
Legyen \displaystyle R tükörképe \displaystyle PB felezőpontjára \displaystyle {R_2} és tekintsük a \displaystyle \mathbf{t}_1 = AP{R_2}B és \displaystyle \mathbf {t}_2 = EKHG törött vonalakat. Megmutatjuk, hogy a megfelelő szakaszok hosszának aránya \displaystyle 2 \lambda, a \displaystyle \bf {t}_2-beli szakaszok iránya a \displaystyle \bf {t}_1-beliek pozitív 90°-os elforgatottja.
\displaystyle AP = \lambda \cdot PE = 2 \lambda \cdot EK ; \displaystyle AP és \displaystyle EP merőlegessége miatt \displaystyle AP és \displaystyle EK merőlegesek. \displaystyle P{R_2} = RB = \lambda \cdot ER = 2 \lambda \cdot KH ; \displaystyle P{R_2} és \displaystyle KH a \displaystyle P{R_2} -vel párhuzamos \displaystyle RB és a \displaystyle KH -val párhuzamos \displaystyle ER merőlegessége miatt merőlegesek. \displaystyle {R_2}B = PR = 2 \cdot PH = 2 \lambda \cdot HG.
\displaystyle HG merőleges \displaystyle PH-ra és így \displaystyle {R_2} B -re is. \displaystyle AP{R_2} és \displaystyle EKH szögek egyenlőek mint nem egymás szögtartományába eső merőleges szárú szögek. Ugyanez áll a \displaystyle P{R_2}B és \displaystyle KHG szögekre.
\displaystyle \bf {t}_2 tehát \displaystyle \bf {t}_1 -ből \displaystyle 2 \lambda -szoros zsugorítással és 90°-os forgatással származtatható, ezért a végpontjaikat összekötő szakaszok, \displaystyle AB és \displaystyle EG merőlegesek. \displaystyle EG és \displaystyle AB metszéspontját \displaystyle Q-val jelölve \displaystyle Q az \displaystyle E pont merőleges vetülete \displaystyle AB-n. \displaystyle FGQ háromszög \displaystyle Q-nál derékszögű. Mivel \displaystyle \it {k_1} -ben \displaystyle FG átmérő, ez azt jelenti, hogy \displaystyle Q rajta van \displaystyle \it {k_1} -en.
|
 |
| Előzmény: [1104] HoA, 2019-10-22 13:04:38 |
|
| [1104] HoA | 2019-10-22 13:04:38 |
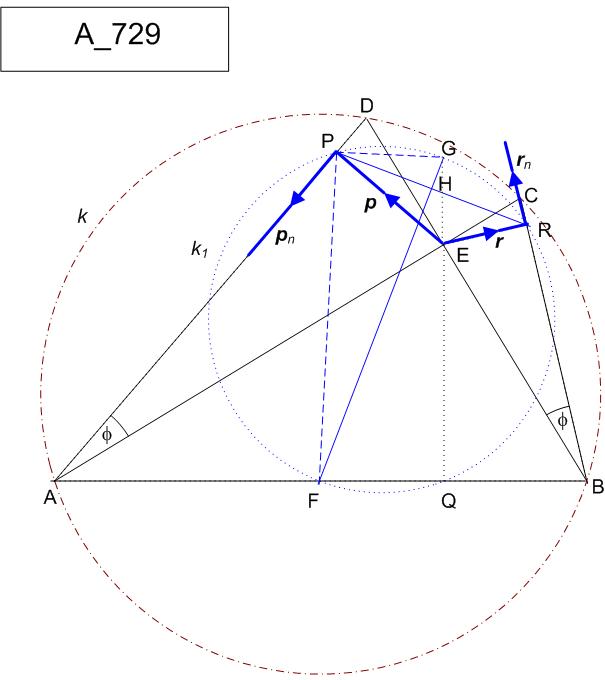
 Az \displaystyle \bf{A 729.} feladat alábbi megoldását azért teszem fel, hogy megmutassam, mindössze két vektor fevételével a feladat megoldásához szükséges szakaszok ( távolságok és irányok ) kifejezhetőek.
\displaystyle APE és \displaystyle BRE derékszögű \displaystyle \Delta-ek hasonlók, mert \displaystyle A-nál ill. \displaystyle B-nél lévő szögük a \displaystyle \it k körülírt kör \displaystyle CD ívéhez tartozó kerületi szög - jelöljük \displaystyle \phi-vel. Legyen \displaystyle BR / RE = AP / PE = ctg \phi = \lambda. \displaystyle E-t origónak választva az \displaystyle \overrightarrow{ER} = r és \displaystyle \overrightarrow{EP} = p vektorokkal ( és a nagybetűs pontok helyvektorait továbbra is a megfelelő vastag kisbetűvel jelölve ) r normálvektora ( +90°os elforgatottja) legyen \displaystyle {\mathbf{r}_n}, p -é \displaystyle {\mathbf{p}_n} Így \displaystyle A és \displaystyle B helyvektorai:
\displaystyle \bf a = {\bf p} + \lambda \cdot \bf {p}_n , \bf b = {\bf r} - \lambda \cdot \bf {r}_n. Felezőpontjuk
\displaystyle \bf{f} = \frac{\mathbf{a}+ \mathbf{b}}2 = \frac{\mathbf{p}+\mathbf{r}}{2}
+ \frac{\lambda}{2} \cdot (\mathbf{p}_n-\mathbf{r}_n)
A \displaystyle PR szakasz \displaystyle H felezőpontja \displaystyle \mathbf{h}= \frac {\bf p + \bf r}{2} , \overrightarrow{RP} = \mathbf{p}-\mathbf{r} ,
\displaystyle \overrightarrow{HP} = \frac{\mathbf{p}-\mathbf{r} }{2} , \displaystyle \overrightarrow{HF} = \mathbf{f}-\mathbf{h} = \frac{\lambda}{2} \cdot (\mathbf{p}_n-\mathbf{r}_n)
Mivel \displaystyle \mathbf{p}_n-\mathbf{r}_n a \displaystyle \mathbf{p}-\mathbf{r} normálvektora, \displaystyle HF és \displaystyle HP merőlegesek, a szakaszok hosszának aránya \displaystyle \lambda . \displaystyle HF a \displaystyle PR felező merőlegese.
Messe az \displaystyle FH egyenes a \displaystyle PFR pontokon áthaladó \displaystyle \it {k_1} kört másodszor \displaystyle G-ben. \displaystyle FG mint húrfelező merőleges \displaystyle \it {k_1} -ben átmérő. \displaystyle \it {k_1} tehát \displaystyle FG Thálesz-köre. \displaystyle FPG \displaystyle \Delta derékszögű, \displaystyle PH az átfogóhoz tartozó magasság. \displaystyle HF / HP = HP / HG = \lambda . \displaystyle HG és \displaystyle HF egy egyenesbe esik, \displaystyle \overrightarrow{HG} = \frac {-1}{\lambda^2} \overrightarrow{HF} = \frac {1}{2 \lambda} (\mathbf{r}_n-\mathbf{p}_n)
\displaystyle \overrightarrow{EG} = \mathbf{g} = \mathbf{h} + \overrightarrow{HG} = \frac {\bf p + \bf r}{2} + \frac {1}{2 \lambda} (\mathbf{r}_n-\mathbf{p}_n)
\displaystyle \overrightarrow{BA} = \mathbf{a}- \mathbf{b} = \mathbf{p}- \mathbf{r} + \lambda \cdot (\mathbf{p}_n + \mathbf{r}_n)
Figyelembe véve, hogy \displaystyle \mathbf{p}_n normálvektora \displaystyle -\mathbf{p}, \displaystyle \mathbf{r}_n -é \displaystyle -\mathbf{r}, \displaystyle \overrightarrow{EG} \displaystyle 2\lambda -szorosának normálvektora éppen \displaystyle \overrightarrow{BA} . Így a \displaystyle GE egyenes egyben az \displaystyle E-ből \displaystyle AB-re bocsátott merőleges. Talppontja legyen \displaystyle Q.\displaystyle FQG derékszögű \displaystyle \Delta, melynek átfogója \displaystyle \it {k_1} \displaystyle FG átmérője, ezért \displaystyle Q rajta van \displaystyle \it {k_1} -en.
|
 |
|
| [1103] Berko Erzsebet | 2019-10-12 06:27:26 |
 C. 1557. 2 típus: Nekem 34 helyett csak 33 jött ki. Írok egy példát. 14: 10, 11, 12, 13, 15, 16, 17, 18, 19, 21, 24, 31, 34, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 51, 54, 61, 64, 71, 74, 81, 84, 91, 94
|
|
| [1102] titok111 | 2019-05-03 12:33:50 |
 Szia!
Legyen a zöld király és a piros alsó rossz helyen.
Ekkor:
A lényeget kiemelve: ZA PA ZK PK
EZ A KIINDULÁS
PA ZA PK ZK (2 LÉPÉS VOLT)
PK ZK PA ZA (EZ IS 2)
ZK PK ZA PA (EZ IS 2)
ZA PK ZK PA
mOST KELLENE A ZK PA CSERE, DE EZT NEM TUDOD MEGCSINÁLNI, MERT MÁS A SZÍNÜK ÉS A SZÁMUK.
|
| Előzmény: [1101] marcius8, 2019-04-28 08:26:47 |
|
| [1101] marcius8 | 2019-04-28 08:26:47 |
 Szép napot mindenkinek! Néhány évvel korábban volt egy felvetésem, amely a pontversenybe is bekerült, mint feladat. Ez a következő volt:
Van egy magyar kártya csomag (32 lap), és a csomagban levő lapokat véletlenszerűen egy 8 sorból és 4 oszlopból álló táblázatban vannak elrendezve. Két lapot akkor lehet megcserélni, ha a két lap ugyanabban a sorban vagy ugyanabban az oszlopban van, továbbá ha a két lap színe vagy értéke megegyezik. Egymás utáni cserékkel el kell érni, hogy a kártyalapok sorrendje rendezett legyen.
A 8 sorból és 4 oszlopból álló kártyacsomag lapjai akkor vannak rendezett sorrendben, ha a következő feltételek teljesülnek: 1.) A táblázat minden oszlopában található négy lap színének sorrendje ebben a sorrendben felülről lefelé haladva: "piros", "tök", "zöld", "makk". 2.) A táblázat minden sorában található nyolc lap értékének sorrendje ebben a sorrendben balról jobbra haladva: "VII", "VIII", "IX", "X", "alsó", "felső", "király", "ász".
Kérdés: Milyen véletlenszerű elrendezésekből érhető el a megengedett cserék egymás utáni alkalmazásával a rendezett állapot? Nekem nagyon véletlenszerű elrendezésből olyan állapot valósult meg, amelyben csak két lap nem volt a helyén, de ez a két lap különböző sorban és különböző oszlopban volt. Ebből az állapotból már nem tudtam elérni a rendezett állapotot, de azt nem tudom, hogy miért nem. Tud nekem ebben valaki segíteni?
|
|
| [1100] Berko Erzsebet | 2019-03-28 04:08:30 |
 K.618. Igazából ehhez a feladathoz azért tettem egy icipici megjegyzést, mert eldönteni azt, hogy az 1 erős-e, számomra egy kicsit kényes kérdés. 1-nél nincs kisebb pozitív egész, az üres halmazra meg minden igaz... Örültem, amikor láttam, hogy a 2-nél nagyobbakat kell sorolni.
|
|
| [1099] Berko Erzsebet | 2019-03-16 07:14:21 |
 Icipici megjegyzés a K. 618. feladathoz. A 2-nél nagyobb erős számokat kellett megkeresni. Az összegzésnél az 1 szerepel.
|
|