Fórum: Lejárt határidejű KÖMAL feladatokról

Kikerülhető a vektoros megoldás általad említett problémája elemi úton, ha észrevesszük, hogy az AA1, BB1, CC1 szakaszok a párhuzamos szelők tételének megfordítása miatt rendre párhuzamosak és kétszeres hosszúságúak, mint az ABC háromszög C-ből, A-ból és B-ből induló súlyvonalai.

Az pedig jól ismert, hogy a háromszög súlyvonalaiból szerkeszthető háromszög.

Mondjuk a hivatalos megoldás is pongyola; nem teljes értékű, mert párhuzamos vektorok összege is lehet nullvektor, és ekkor elfajult háromszög jön csak ki.

Vagyis $\displaystyle 0$ pontosok, jav ...

A B5255. feladatnál tudja valaki, minek tudható be az $\displaystyle 1$ pontos dolgozatok szinte irreálisan magas száma (60)?

Az A.832 feladat központi megoldása szerintem apró hibát tartalmaz. A kérdéses rész a következő:

Legyen $\displaystyle t_n$ annak a valószínűsége, hogy van élő családtag az (n+1)-dik generációban. Ekkor $\displaystyle t_n=1−h_n$, ahol $\displaystyle h_n$ annak a valószínűsége, hogy 0 gyerek születik az n-edik generációban, ami az n-edik generációhoz tartozó $\displaystyle f^{(n)}(x)$ polinom konstans tagja, azaz $\displaystyle h_n=f^{(n)}(0)$

Én úgy gondolom, hogy $\displaystyle f^{(n)}(0)$ annak a valószínűsége, hogy 0 egyed van az n-dik generációban. Tehát annak a valószínűsége, hogy 0 gyerek születik az n-edik generációban: $\displaystyle h_n=f^{(n+1)}(0)$.

Innen persze már jó a bizonyítás, mert $\displaystyle h_{n+1}=f^{(n+2)}(0)=f(h_n)$ továbbra is teljesül.

Ha valamit elnéztem, akkor elnézést kérek.

Illetve végül mégis engedte egy részben...

Már volt szó a fórumon az A.774. feladatról, most szeretnék én is megosztani egy érdekes megoldást, mely nem teljesen a hagyományos geometriai megoldási módszereken alapszik. A méret korlátja miatt két részben teszem fel.

Megoldásvázlat. (Az állítás egyébként csak hegyesszögű háromszögekre igaz.) Legyen az $\displaystyle XYZ$ háromszög beírt körének középpontja $\displaystyle O,$ a $\displaystyle D$ pont merőleges vetületei az $\displaystyle AB,$ $\displaystyle AC$ és $\displaystyle BC$ egyeneseken rendre $\displaystyle T_1,$ $\displaystyle T_2,$ illetve $\displaystyle T_3.$ Legyen továbbá az $\displaystyle ABC$ háromszög magasságpontja $\displaystyle M.$

Nagyítsuk az $\displaystyle X,Y,Z,O,T_1,T_2,T_3$ pontokat kétszeresére $\displaystyle D$-ből, tetszőleges pont képét egy vesszővel jelöljük. Ekkor $\displaystyle X',$ $\displaystyle Y'$ és $\displaystyle Z'$ az $\displaystyle ABC$ háromszög köréírt körére fognak esni (egy körön lévő pont tükröképei egy átmérőre), míg a $\displaystyle T_1T_2T_3$ Simson-egyenes jól ismert módon az $\displaystyle M$ ponton átmenő $\displaystyle T_1'T_2'T_3'$ egyenesbe megy át, mely a $\displaystyle D$ pont oldalakra vett tengelyes tükörképeit tartalmazza. Azt kell belátni, hogy $\displaystyle O'$ ezen rajta van.

Vegyük észre, hogy az $\displaystyle X'Y'Z'$ háromszög szögei állandóak, ahogy $\displaystyle D$ mozog a körülírt körön, ugyanis irányított körívekkel számolva $\displaystyle \widehat{DX'}=2\widehat{DA},$ $\displaystyle \widehat{DY'}=2 \widehat,$ illetve $\displaystyle \widehat{DZ'}=2\widehat{DC},$ azaz $\displaystyle \widehat{X'Y'}=\widehat{DY'}-\widehat{DX'}=2(\widehat{DB}-\widehat{DA}),$ $\displaystyle \widehat{Y'Z'}=2(\widehat{DC}-\widehat{DB}),$ illetve $\displaystyle \widehat{Z'X'}=2(\widehat{DA}-\widehat{DC}),$ azaz pozitív körüljárási irányban a három pont ugyanolyan helyzetben követi egymást, és akkor az általuk kifeszített háromszög is minden helyzetben egybevágó. Mivel a köréírt köre állandó, ezért ha $\displaystyle D$ egyenletes, egységnyi sebességgel mozog a körön, akkor $\displaystyle X'Y'Z'$ is egységnyi sebességgel forog a köréírt kör középpontja körül. Speciálisan ekkor a háromszög beírt körének középpontja, azaz $\displaystyle O$ is egységnyi sebességgel fog forogni.

Nézzük most a $\displaystyle T_1'T_2'T_3'$ egyenest. Ez megegyezik a $\displaystyle T_1'M$ egyenessel (amennyiben ez a két pont nem esik egybe). $\displaystyle T_1'$ az $\displaystyle ABM$ körön mozog, hiszen jól ismert, hogy ez az $\displaystyle ABC$ kör tengelyes tükörképe az $\displaystyle AB$ egyenesre, ráadásul, ha $\displaystyle D$ egységnyi sebességgel mozog, akkor nyilván a tükörkép is egységnyi sebességgel fog mozogni az $\displaystyle ABM$ körön. A kerületi és középponti szögek tétele alapján ekkor a $\displaystyle T_1'T_2'T_3'$ egyenes $\displaystyle \frac12$ sebességgel forog $\displaystyle M$ körül. Akár folytonossággal, akár számítással igazolhatjuk, hogy ha $\displaystyle T_1'$ és $\displaystyle M$ egybeesnek, akkor egyenesünk éppen az $\displaystyle ABM$ körhöz $\displaystyle M$-ben húzott érintő, azaz ebben a helyzetben is igaz, hogy a $\displaystyle T_1'T_2'T_3'$ egyenes fele akkora szöget fordult, mint a $\displaystyle D$ pont (a mozgatás kezdete óta).

Azt kell belátnunk, hogy $\displaystyle O$ mindig rajta van a $\displaystyle T_1'T_2'T_3'$ egyenesen. Vegyük észre, hogy ez biztosan igaz, ha $\displaystyle M$ rajta van azon a körön, amelyen $\displaystyle O$ mozog, ugyanis ekkor fenti megállapításaink szerint $\displaystyle O$ egyszeres sebességgel mozog, míg a $\displaystyle T_1'T_2'T_3'$ egyenes fele sebességgel forog a kör egy pontja körül, és ekkor a kerületi és középponti szögek tétele szerint $\displaystyle O$ mindig rajta lesz az $\displaystyle M$ körül forgó egyenesen.

Ha $\displaystyle D$ éppen egybeesik az $\displaystyle ABC$ háromszög $\displaystyle A$ csúcsával, akkor $\displaystyle X',$ $\displaystyle T_1'$ és $\displaystyle T_2'$ is egybeesnek az $\displaystyle A$ ponttal, azaz a $\displaystyle T_1'T_2'T_3'$ egyenes éppen az $\displaystyle A$-ból $\displaystyle BC$-re állított merőleges (hiszen az $\displaystyle AT_3'$ egyenes a tükrözés miatt merőleges $\displaystyle BC$-re). Másrészt némi szögszámolással (felhasználva, hogy $\displaystyle BY'=BX'\equiv{BA}$ és $\displaystyle CZ'=CX'\equiv{CA},$ hiszen $\displaystyle Y',$ illetve $\displaystyle Z'$ a $\displaystyle D\equiv{X}$ pont $\displaystyle BO$-ra, illetve $\displaystyle CO$-ra vonatkozó tükörképei) könnyen belátható, hogy amennyiben $\displaystyle ABC$ hegyesszögű, akkor az $\displaystyle A$-ból induló magasság, mely a $\displaystyle T_1'T_2'T_3'$ egyenes jelen helyzetben, felezi az $\displaystyle Y'X'Z'$ szöget, mégpedig belső szögfelező (azért nem írom ezt le részletesebben, mert a teljesség igényével itt több különböző esetet kell megvizsgálni a pontok elhelyezkedése szerint, irányított szögekkel csak részben kerülhető el a diszkusszió, azt be kell látni, hogy a kapott szögfelező belső szögfelező, ld. például a tompaszögűek esetén nem az). Így a $\displaystyle T_1'T_2'T_3'$ egyenesen ebben az esetben rajta van $\displaystyle O.$ Hasonlóképp $\displaystyle O$ akkor is rajta van a $\displaystyle T_1'T_2'T_3'$ egyenesen, ha $\displaystyle D$ a háromszög $\displaystyle B$ csúcsával esik egybe. Belátjuk, hogy ez csak úgy lehet, hogy $\displaystyle M$ rajta van az $\displaystyle O$ által befutott körön.

Ugyanis mozgatásunknál megállapítottak alapján $\displaystyle O$ a két helyzet között kétszer akkora szöget tett meg, mint amennyit a $\displaystyle T_1'T_2'T_3'$ egyenes $\displaystyle M$ körül elfordult. Így ha mindkétszer (jelöljük ezeket a helyeket $\displaystyle O_1$-gyel és $\displaystyle O_2$-vel) rajta van az egyenesen, akkor irányított szögekkel $\displaystyle \angle{(MO_1,MO_2)}$ éppen kétszer akkora, mint az $\displaystyle O$ lehetséges helyzetei által alkotott körön vett $\displaystyle \widehat{O_1O_2}$ irányított ívhez tartozó kerületi szög. Így a kerületi és középponti szögek tételének megfordítása miatt $\displaystyle M$ rajta van az $\displaystyle O$ által befutott körön, és a fentiek szerint ebből már adódik az állítás.

Végül pedig visszakicsinyítve a pontokat azt kapjuk, hogy $\displaystyle T_1T_2T_3O$ is kollineáris, és ezt akartuk belátni.

U.i.: Tompaszögű háromszög esetén módosítani kell kicsit az állításon: ekkor a tompaszöggel szemközti hozzáírt kör középponta van rajta a $\displaystyle D$-hez tartozó Simson-egyenesen.

B. 5233. feladat: Ekkor mennyi lehet a hatszög két (szemközti, szomszédos) oldalára írt szám korrelációs együtthatója?

B. 5233. Egy szabályos hatszög csúcsaira véletlenszerű sorrendben felírjuk az 1,2,…,6 számokat. Ezután a hatszög minden oldalára ráírjuk a két végpontján szereplő számok különbségének abszolútértékét. Határozzuk meg az oldalakra írt hat szám összegének várható értékét.

Lejárt A822. feladatnál a közölt megoldáshoz képest a változók felét lehet megspórolni, és sokkal jobban is látható a bizonyítás:

Feltehetö $\displaystyle p=\frac an,q=\frac bn,r=\frac cn$ ekkor $\displaystyle a+b+c=0$ és $\displaystyle a*b*c=n^3$ azaz: $\displaystyle a*b*(a+b)=-n^3$

legyen lnko(a,b)=g, ekkor $\displaystyle a=g*u,b=g*v$ és itt már lnko($\displaystyle u,v$)=$\displaystyle 1$, itt $\displaystyle a,b$ értékét beírva kapjuk:

$\displaystyle g^3*u*v*(u+v)=-n^3$

azaz $\displaystyle u*v*(u+v)=d^3$ ahol $\displaystyle d=-\frac ng$-nek egésznek kell lennie. Triviálisan u,v,u+v páronként relatív prím.

Így a szorzat minden tagja köbszám: $\displaystyle u=x^3,v=y^3,u+v=z^3$ és így: $\displaystyle x^3+y^3=z^3$ valamely $\displaystyle x,y,z$ nemnulla egészekre ami a Fermat egyenlet spec esete, nincs megoldása.

Lejárt A812. megoldása pongyola, hiányzik a bizonyításból, hogy teljes indukciót alkalmazunk, például az $\displaystyle n+k$ összegre.

Eredeti megfogalmazásomban a következőképpen nézett ki az előbb felvetett probléma, amelyet Kós Géza Tanár Úr átfogalmazott, és a KöMaL-pontversenybe került be: (érdekes matek feladatok, [3668])

Egy játékot találtam ki. Mivel egy játékkal akkor foglalkoznak sokan, ha szabályai egyszerűek, ugyanakkor nem könnyen végigjátszható, ezért a következő játékot találtam ki:

A magyar kártyacsomag összetétele: A magyar kártyacsomag 32 lapot tartalmaz. Minden lapnak van színe és értéke. A színek lehetnek: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél). Az értékek lehetnek: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”. A kártyacsomagban minden lehetséges szín-érték párosítás előfordul.

A nyolc sorból és négy oszlopból álló táblázatban elhelyezett magyar kártyacsomag lapjai akkor vannak rendezett sorrendben, ha a következő feltételek teljesülnek:

• A táblázat minden oszlopában található négy lap színének sorrendje felülről lefelé haladva: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél).

• A táblázat minden sorában található nyolc lap értékének sorrendje balról jobbra haladva: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”.

A játék szabálya: A kártyacsomag lapjai véletlenszerű sorrendben egy négy sorból és nyolc oszlopból álló táblázatban vannak elhelyezve. A játék során egyszerre mindig két lapot lehet megcserélni. Két lapot csak akkor lehet megcserélni, ha a két lap ugyanabban a sorban vagy ugyanabban az oszlopban van, továbbá (és) ha a két lap színe vagy értéke ugyanaz. A játék célja, hogy a kártyalapok sorrendje rendezett legyen.

Az érdekes az hogy a véletlenszerűen összekevert állapotból majdnem mindig abba az állapotba jutok, hogy a rendezett állapothoz képest a "makk ász" és a "tök király" fel van cserélve. Sajnos, nem tudok rájönni, hogy ez az én ügyetlenségem (gyanítom, hogy igen), de ugyanakkor nem hiszem hogy ennek törvényszerűen így kell lenni. Arra kérek bárkit, hogy ha ezt a jelenséget meg tudja indokolni, vagy meg tudja oldani (tehát ha a rendezett állapothoz képest csak a "makk ász" és a "tök király" van felcserélve, akkor ez az állapot rendezhető vagy sem), írjon a marcius.08@freemail.hu címre.

A következő feladat megoldását keresem. Annak idején ezt a problémát én vetettem fel a fórumban, de akkor sem tudtam a megoldását, egy passziánsz játékot terveztem számítógépre, Kós Géza Tanár Úr tette be a kömal-pontversenybe. Ha valaki el tudná küldeni ennek a feladatnak a megoldását, nagyon megköszönöm. A feladatot kicsit átfogalmaztam annyiban, hogy más betűjeleket használok, illetve egy kérdést hozzátettem.

A. 585. (2013 március) Adottak az $\displaystyle i_0\ge2$, $\displaystyle j_0\ge2$ egész számok. Az $\displaystyle (i,j)$ számpárokat, ahol $\displaystyle 1\le{i}\le{i_0}$, $\displaystyle 1\le{j}\le{j_0}$ egészek, ráírtuk egy-egy kártyára úgy, hogy mindegyik pár pontosan egy kártyán szerepeljen. Ezután a következő játékot játsszuk: Az $\displaystyle i_0*j_0$ darab kártyát elhelyezzük egy $\displaystyle i_0×j_0$-ás táblázatban úgy, hogy minden $\displaystyle i$-re és $\displaystyle j$-re az $\displaystyle (i,j)$ kártya az $\displaystyle i$-edik sorban és a $\displaystyle j$-edik oszlopban legyen, tekintsük ezt az elrendezést természetesnek. Az $\displaystyle (i_1,j_1)$ és $\displaystyle (i_2,j_2)$ kártyákat felcserélhetjük, ha ugyanabban a sorban vagy ugyanabban az oszlopban vannak, és $\displaystyle i_1=i_2$ vagy $\displaystyle j_1=j_2$.

Elérhetjük-e ilyen lépésekkel, hogy pontosan két kártya helyet cseréljen, a többi kártya pedig visszakerüljön a kiinduló helyére? És mi annak a szükséges és elégséges feltétele, hogy egy $\displaystyle i_0×j_0$-ás táblázatban tetszőlegen elhelyezett kártyákat a megengedett felcserélésekkel természetes sorrendbe lehet rendezni?

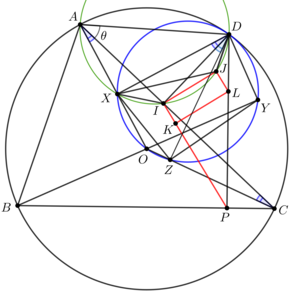
I post my solution to the problem A. 774 because it shows that the problem is one of the few applications of the Japanese theorem.

Let $\displaystyle I$ be the projection of the point $\displaystyle D$ on the line $\displaystyle AC$.
Let $\displaystyle J$, $\displaystyle K$ and $\displaystyle L$, respectively be the incenters of the triangles $\displaystyle \Delta XDY$, $\displaystyle \Delta XYZ$ and $\displaystyle \Delta DYZ$, respectively.
From $\displaystyle DX\perp AO,\; DY\perp BO,\; DZ \perp CO$ it follows that

$\displaystyle D,O,X,Y,Z\text{ lies on the circle of diameter } DO\tag{1}$

Let $\displaystyle P$ be the projection of $\displaystyle D$ on the line $\displaystyle BC$, $\displaystyle A=\measuredangle BAC$ and similarly we define $\displaystyle B$ and $\displaystyle C$, let $\displaystyle \theta=\measuredangle DAC$.
From $\displaystyle (1)$ it follows that $\displaystyle \measuredangle XDI=\measuredangle OAC=\measuredangle OCA=\measuredangle ZDI\Rightarrow$

$\displaystyle \measuredangle XDI=\measuredangle ZDI\tag{2}$

From $\displaystyle (1)$ it follows that $\displaystyle \measuredangle DXZ=180^\circ- \measuredangle DOZ=\measuredangle DOC=2\measuredangle CAD=\measuredangle DXI$, which implies $\displaystyle \measuredangle DXI=\measuredangle ZXI$. From this and $\displaystyle (2)$ it follows that

$\displaystyle I\text{ is the incenter of the triangle } XDZ\tag{3}$

From $\displaystyle (1)$ it follows that

$\displaystyle \measuredangle XDJ=\frac12\measuredangle XDY=\frac12(180^\circ-\measuredangle XOY)=\frac12\measuredangle AOB =C.$

But from $\displaystyle \measuredangle ADI=90^\circ-\theta$ it follows that $\displaystyle \measuredangle ADX=90^\circ-\theta-(90^\circ-B)=B-\theta$. From this and $\displaystyle \measuredangle ADJ=\measuredangle ADX+\measuredangle XDJ$ it follows that

$\displaystyle \measuredangle ADJ=B-\theta+\measuredangle XDJ{=} B+C-\theta=180^\circ-A-\theta\tag{4}$

From $\displaystyle (3)$ it follows that

$\displaystyle \measuredangle XUD=90^\circ + \frac12\measuredangle XZD=90^\circ + \frac12\measuredangle XYD=\measuredangle XJD,$

which implies that the quadrilateral $\displaystyle XIJD$ is cyclic. From this and $\displaystyle (1)$ it follows that the points $\displaystyle X,I,J,A,D$ are concyclic, which implies $\displaystyle \measuredangle AIJ=180^\circ-\measuredangle ADJ$. From this and $\displaystyle (4)$ it follows that $\displaystyle \measuredangle AIJ=A+\theta=\measuredangle BAD$.
From this and $\displaystyle (1)$ it follows that

$\displaystyle \measuredangle PIC=\measuredangle PDC=90^\circ-\measuredangle DCP=90^\circ-(180^\circ-\measuredangle BAD)=\measuredangle BAD-90^\circ$

$\displaystyle =\measuredangle AIJ-90^\circ=\measuredangle AIJ-\measuredangle DIA=\measuredangle DIJ,$

which implies

$\displaystyle \measuredangle PIJ= \measuredangle PIC+\measuredangle CIJ=\measuredangle DIJ+\measuredangle CIJ=\measuredangle CID=90^\circ\tag{5}$

From $\displaystyle (1)$, $\displaystyle (3)$ and the Japanese theorem in $\displaystyle DXYZ$ it follows that $\displaystyle IJKL$ is rectangle, which implies $\displaystyle \measuredangle KIJ=90^\circ$. From this and $\displaystyle (5)$ it follows that $\displaystyle K\in PI$, which is the $\displaystyle P$-Simson line in $\displaystyle \Delta ABC$. Thus, we have solved the problem.

Üdv! Két kérdésem lenne a szeptemberi fizikafeladatok megoldásával kapcsolatban. Egyrészt a P. 5340-ben az ábra szerint végig vöröseltolódik a hullám a 45 perces periódusokban, amikor nem takarja a bolygó. Tehát a hullámforrás végig távolodik tőlünk. De a megoldás szerint körpályán kering a műhold a bolygója körül. Ebben nincs ellentmondás? Mármint akkor egy ideig közelednie kéne, nem? Javítsatok ki, ha tévedek.

A másik ,hogy a P. 5344.-ben ez: "amiből készült hasábot a prizma másik oldalához illesztve a törési szög az ábra szerint α/2" áll a feladat szövegében. De a megoldás így számol: "Ha a prizmából kilépő fény törési szöge 16,6∘"... A feladat szövege alapján az

üvegből kilépő fény törési szöge α/2, legalábbis szerintem. És akkor a törésmutatója az üvegnek a sinus(béta) és a sinus (α/2 ) hányadosa.

Part 2.
We prove that $\displaystyle 1\leqslant r\leqslant p-2\Rightarrow P(1)\equiv 0$.
We note that

$\displaystyle \widehat{x}_1,..., \widehat{x}_n \text{ are roots (in \(\displaystyle \mathbb{Z}_p\)) of the polynomial } P\tag{4}$

First, we prove the following proposition by induction on $\displaystyle k\in \mathbb{Z}, k\geqslant 1$:

$\displaystyle \mathcal{P}(k): \;\; k\binom{r}{k}=r\sum_{j=0}^{k-1} (-1)^{k-j+1}\binom{r}{j}.$

Induction Base. $\displaystyle k=1: \; \binom{r}{1}=r\cdot (-1)^2\binom{r}{0}$.
Induction Step. $\displaystyle k\mapsto (k+1)$. Using induction hypothesis, we compute

$\displaystyle (k+1)\binom{r}{k+1} =(k+1)\frac{r-k}{k+1}\binom{r}{k}= r\binom{r}{k}-k\binom{r}{k}$

$\displaystyle =r\binom{r}{k}-r\sum_{j=0}^{k-1}(-1)^{k-j+1}\binom{r}{j} =r\sum_{j=0}^k(-1)^{k-j+2}\binom{r}{j}.$

Induction finished.
Secondly, we prove that $\displaystyle e_k\equiv\binom{r}{k}$ by induction on $\displaystyle k, 1\leqslant k\leqslant p-2$.
Induction Base is trivial.
Induction Step. $\displaystyle k\mapsto (k+1)$. Because $\displaystyle k+1\leqslant p-2$ and hypothesis it follows that for each $\displaystyle 1\leqslant i\leqslant k+1$ we have $\displaystyle s_i\equiv r$. From this and $\displaystyle (3)$ it follows that

$\displaystyle (k+1)e_{k+1}\equiv r\sum_{i=1}^{k+1}(-1)^{i-1}e_{k+1-i}\equiv r \sum_{I=1}^{k+1}(-1)^{i-1}\binom{r}{k+1-i}$

$\displaystyle \equiv r\sum_{j=0}^{k}(-1)^{k-j+1}\binom{r}{j}\stackrel{\mathcal{P}}{=}(k+1) \binom{r}{k+1},$

which implies $\displaystyle e_{k+1}\equiv\binom{r}{k+1}$. Induction finished. Hence

$\displaystyle \forall k, \; 1\leqslant k\leqslant p-2\Rightarrow e_k\equiv\binom{r}{k}\tag{5}$

By $\displaystyle (5)$ for $\displaystyle k=r+1\leqslant p-2$ it follows that

$\displaystyle e_{r+1}\equiv 0\tag{6}$

From the Newton-Girard identities in second case it follows that

$\displaystyle \sum_{I=1}^{p+r}(-1)^{i-1}e_{p+r-i}s_i=0\tag{7}$

By the hypothesis $\displaystyle \forall 1\leqslant k\leqslant p-2:\; s_k\equiv r$ and Fermat's Little Theorem it follows that for each $\displaystyle 1\leqslant k\leqslant p-2$:

$\displaystyle s_{p+k-1}=\sum_{j=1}^nx_j^{p+k-1}=\sum_{j=1}^nx_j^{p-1}\cdot x_j^k\equiv \sum_{j=1}^n x_j^k=s_k\equiv r \Rightarrow$

$\displaystyle s_1\equiv s_2\equiv \ldots \equiv s_{p-2}\equiv s_p\equiv\ldots\equiv s_{2p-3}\equiv r\tag{8}$

From $\displaystyle (6)$ it follows that $\displaystyle e_{r+1}=0$, which implies $\displaystyle e_{p+r-(p-1)}s_{p-1}=e_{r+1}s_{p-1}=0$. From this, $\displaystyle p+r\leqslant 2p-3$ and $\displaystyle (7)$ and $\displaystyle (8)$ it follows that $\displaystyle 0\equiv r\sum_{i=1}^{p+r}(-1)^{i-1}e_{p+r-i}$. Because $\displaystyle r\neq 0$ it follows that

$\displaystyle 0\equiv \sum_{i=1}^{p+r}(-1)^{i-1}e_{p+r-i}=e_0-e_1+e_2-\ldots+(-1)^{p+r-1}e_{p+r-1}=P(1).$

Hence $\displaystyle P(1)\equiv 0$.

Now, we prove by induction on $\displaystyle r\in \{0,1,\ldots,p-3\}$ that the solutions to the problem are $\displaystyle (\underbrace{1,1,\ldots,1}_{\times r},\underbrace{0,0,\ldots,0}_{\times (p-1)}) \text{ and } (\underbrace{1,1,\ldots,1}_{\times r},1,2,\ldots,p-1)$.
Induction Base is the case $\displaystyle r=0$.
Induction Step. $\displaystyle r\mapsto (r+1)$. Because $\displaystyle \widehat{x}_1,...,\widehat{x}_{p+r}$ are the roots (in $\displaystyle \mathbb{Z}_p$) of the polinomial $\displaystyle P$ and $\displaystyle P(1)\equiv 0$ it follows that $\displaystyle \widehat{1}\in \{\widehat{x}_1,\ldots, \widehat{x}_{p+(r+1)-1}\}$.
WLOG we can assume that $\displaystyle x_{p+r}\equiv 1$. From this and the hypothesis it follows that $\displaystyle \forall 1\leqslant k\leqslant p-2$:

$\displaystyle r+1 \equiv \sum_{j=1}^{p+r}x_j^k\equiv 1+\sum_{j=1}^{p+r-1}x_j^k\pmod p.$

From this and the induction hypothesis it follows that the solutions are

$\displaystyle (\underbrace{1,1,...,1}_{\times r},\underbrace{0,0,...,0}_{\times(p-1)},1) \text{ and } (\underbrace{1,1,\ldots,1}_{\times r},1,2,\ldots,p-1,1),$

which finished the induction. The problem is solved!

This is an alternative proof for the problem A. 792., which is based on an idea found in January (to use the Newton's identities), which I could not complete at that time.
(Because I'm authorized to post up to 5120 characters I post the solution in two parts).

Part 1. Let $\displaystyle n=p+r-1$. Let

$\displaystyle e_0=1,\;e_1=\sum_{i=1}^n x_i,\; e_2=\sum_{1\leqslant i<j\leqslant n} x_ix_j,... ,\; e_n=\prod_{i=1}^ne_i.$

Let (in $\displaystyle \mathbb{Z}_p$) be the polynomial $\displaystyle P(x)=\prod_{i=1}^n(x-x_i)=\sum_{k=0}^n(-1)^{n-k}x^{k}e_{n-k} \in \mathbb{Z}_p[x]$ (we use $\displaystyle \mathbb{Z}_p$ instead of $\displaystyle \mathbb{F}_p$).
For each positive integer $\displaystyle k$ let $\displaystyle s_k=\sum_{j=1}^n x_j^k$. Let $\displaystyle \mathbb{Z}_p^*=\mathbb{Z}_p\setminus \{\widehat{0}\}$. We abreviatte $\displaystyle a\equiv b\;(\mathrm{mod} \; p)$ by $\displaystyle a\equiv b$.
First we solve the problem in
The Case $\displaystyle r=0$. From Newton-Girard identities it follows that

$\displaystyle \forall k\in \mathbb{Z}, 1\leqslant k\leqslant p-1: \; \; ke_k= \sum_{i=1}^k (-1)^{i-1}e_{k-i}s_i \tag{1}$

By the hypothesis

$\displaystyle s_1\equiv s_2\equiv ...\equiv s_{p-2}\equiv 0 \tag{2}$

We prove by induction on $\displaystyle k \in \{1,2,...,p-2\}$ that $\displaystyle e_k\equiv 0$.
Induction Base. $\displaystyle e_1=s_1 \equiv 0 \Rightarrow e_1\equiv 0$.
Induction Step. $\displaystyle k \mapsto (k+1)$. From $\displaystyle (1)$ it follows that

$\displaystyle (k+1)e_{k+1}=\sum_{i=1}^{k+1} (-1)^{i-1}e_{k+1-i}s_i\tag{3}$

Because for each $\displaystyle 1\leqslant i\leqslant k+1$: $\displaystyle {k+1-i}\in \{0,1,...,k\}$, $\displaystyle (2)$, $\displaystyle (3)$ and because $\displaystyle k+1\leqslant p-2$ it follows that

$\displaystyle (k+1)e_{k+1}\equiv 0.$

Hence $\displaystyle e_{k+1}\equiv 0$. Induction finished.
Hence $\displaystyle \widehat{x}_1,..., \widehat{x}_{p-1}$ are roots of the polynomial $\displaystyle P(x)=x^{p-1}-\widehat{e}_{p-1}$ in $\displaystyle \mathbb{Z}_p$. We have 2 sub-cases:
1. $\displaystyle e_{p-1}\equiv 0 \Rightarrow \widehat{x}_1,..., \widehat{x}_{p-1}$ are roots of the polynomial $\displaystyle x^{p-1}$ in $\displaystyle \mathbb{Z}_p$, which implies $\displaystyle x_1\equiv x_2\equiv ...\equiv x_{p-1}\equiv 0$.
2. $\displaystyle e_{p-1}\not\equiv 0$. Then $\displaystyle x_i\not\equiv 0$ for each $\displaystyle 1\leqslant i\leqslant p-1$.
By Fermat's Little Theorem $\displaystyle \forall t\in \mathbb{Z}_p^*$: $\displaystyle t^{p-1}\equiv 1$ it follows that $\displaystyle P(x)=x^{p-1}-\widehat{e}_{p-1}$ have roots in $\displaystyle \mathbb{Z}_p$ if and only if $\displaystyle e_{p-1}\equiv 1$. Hence

$\displaystyle x^{p-1}-\widehat{e}_{p-1}=x^{p-1}-\widehat{1}= (x-\widehat{1})(x-\widehat{2})...(x-\widehat{p-1}),$

which implies $\displaystyle \{\widehat{x}_1,\ldots, \widehat{x}_{p-1}\}=\mathbb{Z}_p^*$.
Case $\displaystyle r=0$ finished.

Thank you! Euler circle (nine-point circle) is Feuerbach circle.

Köszönöm, szép megoldás!

Elegant, thx! (Euler circle=Feuerbach circle?)

Bemásolom Michael Rozenberg bizonyítását.

(A [902]-ben látott elegáns megoldás nekem jobban tetszik.)

A "szép" megoldás: ugyanezen fórumtéma [902] hozzászólás

A kicsit csúnya megoldás: ugyanezen fórumtéma [898] megoldás

Ha $\displaystyle x=0$ vagy $\displaystyle y=0$ akkor az állítás trivi. Egyébként feltehető, hogy $\displaystyle x*y=1$ vagy $\displaystyle x*y=-1$ ez is trivi. Tehát egy változótól meg tudnánk szabadulni, még nehéz marad a probléma, nem?

Kicsit késve, de én is felteszek egy megoldás(vázlato)t az A.796. feladatra.

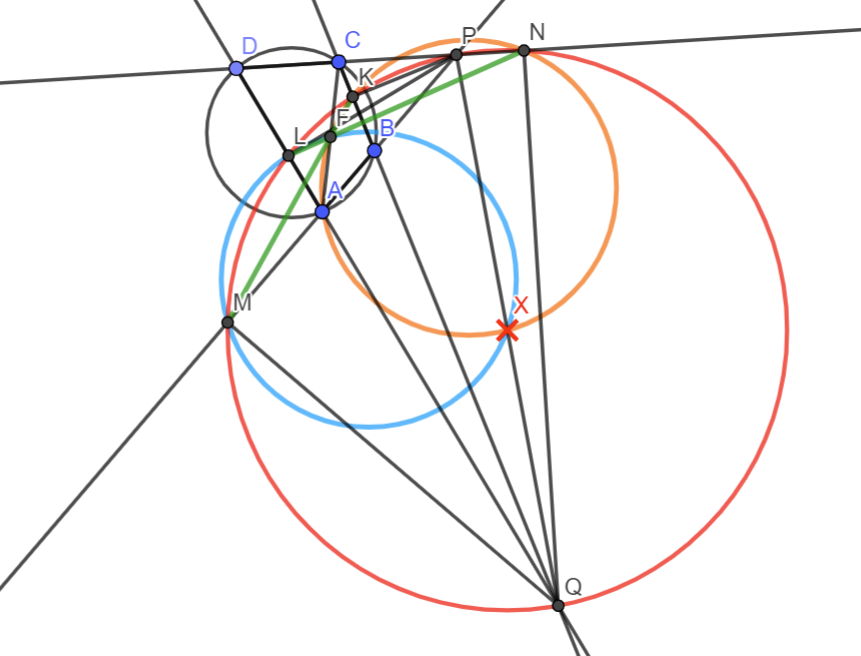
Megoldás(vázlat). Az ábrának számtalan különböző példánya lehet, ezért a diszkusszió elkerülése érdekében végig irányított szögeket fogunk használni. (Tehát az $\displaystyle XYZ\sphericalangle$ jelölés azt fogja jelenteni, hogy mekkora szöggel kell az $\displaystyle XY$ egyenest elforgatni pozitív irányba, hogy az $\displaystyle YZ$ egyenest kapjuk.) Jelölje $\displaystyle X$ a $\displaystyle PQ$ szakasz felezőpontját, megmutatjuk, hogy $\displaystyle X$ az $\displaystyle FKN$ és $\displaystyle FLM$ körök második metszéspontja. Először is megjegyezzük, hogy a Thalesz-tétel miatt $\displaystyle K,L,M,N$ a $\displaystyle PQ$ szakasz fölé emelt Thalesz-körön vannak, és ennek a középpontja $\displaystyle X.$ Két lemma adja a megoldás kulcsát.

Első lemma. A $\displaystyle KMF,$ illetve $\displaystyle LFN$ ponthármasok kollineárisok.

Bizonyítás. A szimmetriára szorítkozva elég belátnunk, hogy $\displaystyle KMF$ egy egyenesre esnek. Irányított szögekkel: $\displaystyle PBK\sphericalangle=-QBM\sphericalangle,$ illetve $\displaystyle KCP\sphericalangle=BCP\sphericalangle=BCD\sphericalangle=BAD\sphericalangle=MAQ\sphericalangle.$ Így tehát $\displaystyle PKB\triangle\sim{QMB}\triangle,$ és ezek ellentétetes körüljárási irányúak, illetve $\displaystyle PKC\triangle\sim{QMA}\triangle,$ és ezek azonos körüljárási irányúak. Ebből adódik, hogy -előjeles szakaszokkal- $\displaystyle \frac{BK}{KC}=-\frac{BM}{MA}.$ Tehát $\displaystyle \frac{AF}{FC}\cdot{\frac{CK}{KB}}\cdot{\frac{BM}{MA}}=-1,$ amiből a Menelaosz-tétel megfordítása miatt az következik, hogy $\displaystyle K,M$ és $\displaystyle F$ egy egyenesre esnek. Hasonlóképp látható be ez az $\displaystyle LFN$ pnthármasról is. $\displaystyle \square$

Második lemma. $\displaystyle KL\parallel{MN}.$

Bizonyítás. Ha sikerülne belátni, hogy $\displaystyle MNP\sphericalangle+NPK\sphericalangle=LKP\sphericalangle,$ akkor teljesülne a bizonyítandó, hiszen $\displaystyle LKP\sphericalangle=-PKL\sphericalangle,$ így $\displaystyle MNP\sphericalangle+NPK\sphericalangle+PKL\sphericalangle=0°,$ azaz $\displaystyle MN$ és $\displaystyle KL$ párhuzamosak. Mivel (a kerületi szögek irányított szögekre vonatkozó tétele alapján) $\displaystyle MNP\sphericalangle=MQP\sphericalangle$ és $\displaystyle LKP\sphericalangle=LQP\sphericalangle,$ ezért $\displaystyle LKP\sphericalangle-MNP\sphericalangle=LQP\sphericalangle-MQP\sphericalangle=LQM\sphericalangle.$ Így elég azt bizonyítani, hogy $\displaystyle LQM\sphericalangle=NPK\sphericalangle.$ Legyen $\displaystyle I=PK\cap{QN}.$ Ekkor $\displaystyle N$ és $\displaystyle K$ a $\displaystyle CI$ fölé rajzolt Thalesz-körön vannak, azaz $\displaystyle N,K,C,I$ egy körön vannak. Innen $\displaystyle LQM\sphericalangle=90°-MAQ\sphericalangle=90°-BAD\sphericalangle=90°-BCD\sphericalangle=$ $\displaystyle =90°-KCN\sphericalangle=90°-KIN\sphericalangle=NPK\sphericalangle.$ Ezzel a fentiek szerint beláttuk a második lemmát. $\displaystyle \square$

A két lemma alapján $\displaystyle KLMN$ (nem feltétlen ilyen sorrendben a csúcsokkal) húrtrapéz, $\displaystyle F$ a szárai vagy az átlói metszéspontja. A lemmák alapján $\displaystyle KMN\sphericalangle=KQN\sphericalangle$ és $\displaystyle MNL\sphericalangle=MQL\sphericalangle,$ így $\displaystyle NFM\sphericalangle=-KQN\sphericalangle-MQL\sphericalangle.$ Mivel a szimmetria miatt a $\displaystyle KQN\sphericalangle$ és $\displaystyle MQN\sphericalangle$ nagysága azonos (azonos nagyságú íven -a húrtrapéz oldala vagy átlója- nyugszanak), és irányításuk is azonos, ezért $\displaystyle NFM\sphericalangle=NFK\sphericalangle=LFM\sphericalangle=-2KQN\sphericalangle=-2MQL\sphericalangle.$ Innen $\displaystyle NFK\sphericalangle=2NQK\sphericalangle,$ illetve $\displaystyle LFM\sphericalangle=2LQM\sphericalangle,$ amiből a kerületi és középponti szögek tételének megfordítása miatt az $\displaystyle FKN$ és $\displaystyle FLM$ körök is áthaladnak a $\displaystyle KLMNPQ$ kör középpontján, ami az $\displaystyle X$ pont. Ezzel az állítást beláttuk.

Van-e valakinek megoldása, ötlete a 2014. áprilisi számban megjelent A. 616. feladatra?

Proof for the problem A. 796.

For each triangle $\displaystyle XYZ$ let $\displaystyle \mathcal{C}_{XYZ}$ be the circumcircle of the triangle $\displaystyle XYZ$.
Let $\displaystyle A',\, Q',$ and $\displaystyle P'$ be the midpoints of the segments $\displaystyle [PQ],\, [AP],$ and $\displaystyle [AQ]$, respectively. Let $\displaystyle \{H\}=PL \cap QM$ and $\displaystyle \{H'\}=PK\cap QN$ be the orthocenters of the triangles $\displaystyle APQ$ and $\displaystyle CPQ$, respectively.
Let $\displaystyle \mathcal{H}_1$ be the homothety with center $\displaystyle A$ and ratio $\displaystyle 1/2$. Let $\displaystyle E_a$ be the midpoint of the segment $\displaystyle [AH]$.
Because $\displaystyle \{H\}=PL \cap QM$ and $\displaystyle AL\perp LH,\, AM\perp MH$ it follows that the quadrilateral $\displaystyle HLAM$ is cyclic. From this and $\displaystyle ABCD$ is a cyclic quadrilateral it follows that

$\displaystyle \measuredangle QHP=\measuredangle MHL=180^\circ-\measuredangle MAL= 180^\circ-\measuredangle BAD=\measuredangle BCD=\measuredangle QCP,$

which implies that

$\displaystyle \text{the quadrilateral } HCPQ\text{ is cyclic} \tag{1}$

We note that $\displaystyle \mathcal{H}_1(C)=F,\, \mathcal{H}_1(H)=E_a,\,\mathcal{H}_1(Q)=P',\,\mathcal{H}_1(P)=Q'.$ From this and $\displaystyle (1)$ it follows that $\displaystyle \mathcal{H}_1(HCPQ)=E_aFQ'P'$ is a cyclic quadrilateral, which implies that $\displaystyle F$ lies on the Euler circle (nine-point circle) $\displaystyle \mathcal{E}_1$ if the triangle $\displaystyle APQ$.
Because $\displaystyle M\in \mathcal{E}_1$ and $\displaystyle L\in \mathcal{E}_1$ it follows that

$\displaystyle \mathcal{C}_{FLM}=\mathcal{E}_1 \tag{2}$

Similarly to $\displaystyle (2)$, using the homothety $\displaystyle \mathcal{H}_2$ with center $\displaystyle C$ and ratio $\displaystyle 1/2$ we obtain that

$\displaystyle \mathcal{C}_{FKN}=\mathcal{E}_2 \tag{3}$

when $\displaystyle \mathcal{E}_2$ is the Euler circle in the triangle $\displaystyle CPQ$. Because $\displaystyle A'\in \mathcal{E}_1\cap\mathcal{E}_2$ and $\displaystyle A'\in PQ$, from $\displaystyle (2)$ and $\displaystyle (3)$ it follows that $\displaystyle A'\in \mathcal{C}_{FLM}\cap\mathcal{C}_{FKN}\cap PQ,$ which implies the circumcircles of triangles $\displaystyle FKN$ and $\displaystyle FLM$, and the line $\displaystyle PQ$ are concurrent.