| [1173] marcius8 | 2023-04-13 20:31:17 |
 B.5309 Szerkesszük meg a parabola fókuszpontját és vezéregyenesét, ha adott a tengelye és két pontja.
Legyen t a tengely, legyenek az adott pontok: P1 illetve P2.
A két pontnak a tengelytől mért távolsága pontosan akkor egyenlő, ha a két pontnak a tengelyre eső merőleges vetülete egybeesik. Ebben az esetben a parabola nem egyértelmű.
A továbbiakban az adott pontoknak a tengelytől mért távolsága különböző. Legyen a P1 pont a tengelyhez közelebb, a P2 pont a tengelytől távolabb.
Legyen d1 a P1 pontnak a t tengelytől mért távolsága. Legyen d2 a P2 pontnak a t tengelytől mért távolsága. Ekkor d2>d1 teljesül. Legyen Q1 a P1 pontnak a t tengelyre eső merőleges vetülete. Legyen Q2 a P2 pontnak a t tengelyre eső merőleges vetülete. Legyen d az adott pontoknak a t tengelyre eső merőleges vetületeinek távolsága, azaz d=Q1Q2 Legyen Q a Q1Q2 szakasz felezőpontja, a Q pont egyenlő a P1P2 szakasz P felezőpontjának a parabola t tengelyére eső merőleges vetületével.
Helyezzük el a síkbeli derékszögű koordináta-rendszert úgy, hogy az y-tengely egybeessen a t tengellyel, a parabola T tengelypontja az origóban legyen, az adott pontok az x-tengely felett legyenek. Ekkor a tengelytől távolabbi pont az x-tengelytől is távolabb van. Legyen a keresett parabola paramétere p. Ekkor a keresett parabola egyenlete ebben a koordináta-rendszerben: 2py=x2.
A Q1Q2 szakasz Q felezőpontja valahol az y-tengelyen van, legyen a Q1Q2 szakasz Q felezőpontjának második koordinátája d0. Ekkor az adott pontok ebben a koordináta-rendszerben: P1(d1;d0−d/2), P2(d2;d0+d/2).
A P1 pont rajta van a 2p∗y=x2 egyenletű parabolán, így 2p(d0−d/2)=d21.
A P2 pont rajta van a 2p∗y=x2 egyenletű parabolán, így 2p(d0+d/2)=d22.
A két egyenletet kivonva egymásból: 2p∗d=d22−d21.
A két egyenletet összeadva: 4p∗d0=d22+d21, innen p∗d0=(d22+d21)/4
A P1P2 szakasz felezőmerőlegesének egyenlete:
-A P1P2 szakasz felezőpontja: ((d2+d1)/2;d₀)
-A P1 pontból a P2 pontba mutató vektor: ((d2−d1);d)
egyenlet: (d2−d1)∗x+d∗y=(d2−d1)∗(d2+d1)/2+d∗d0
zárójel-felbontás: (d2−d1)∗x+d∗y=(d22−d21)/2+d∗d0
Figyelembe véve, hogy d22−d21=2p∗d, innen (d22−d21)/2=p∗d, a felezőmerőleges egyenlete a következőképpen írható: (d2−d1)∗x+d∗y=p∗d+d∗d0
kiemelés: (d2−d1)∗x+d∗y=d∗(p+d0)
A P1P2 szakasz felezőmerőlegese az y-tengelyt az M pontban metszi, ahol M koordinátái: M(0;p+d0).
A Q pont koordinátái: Q(0;d0).
A Q és M pontok távolsága: QM=p.
A segédtétel értelmében, ha megszerkesztjük a P1P2 szakasz felezőmerőlegesének és a tengely M metszéspontját, majd a P1P2 szakasz P felezőpontjának megszerkesztjük a tengelyre eső merőleges vetületét, legyen ez a Q pont, akkor a QM szakasz éppen a parabola paramétere. Ezután a d1 és d2 szakaszok ismeretében a (d22+d21)1/2 szakasz szerkeszthető (pitagorasz-tétel), így a d0=(d22+d21)/(4∗p) szakasz is szerkeszthető (pl. magasságtétel derékszögű háromszögben, vagy párhuzamos szelők tétele).
|
|
| [1172] marcius8 | 2023-04-13 19:46:52 |
 A B.5306 megfogalmazása szerintem pontatlan volt.
Legyen p₁ annak a valószínűsége, hogy a kocka dobás után 1-est mutat. Legyen p₂ annak a valószínűsége, hogy a kocka dobás után 2-est mutat. Legyen p₃ annak a valószínűsége, hogy a kocka dobás után 3-ast mutat. Legyen p₄ annak a valószínűsége, hogy a kocka dobás után 4-est mutat. Legyen p₅ annak a valószínűsége, hogy a kocka dobás után 5-öst mutat. Legyen p₆ annak a valószínűsége, hogy a kocka dobás után 6-ost mutat.
Legyen q₁ annak a valószínűsége, hogy a pénzérme dobás után 1-est mutat. Legyen q₂ annak a valószínűsége, hogy a pénzérme dobás után 2-est mutat.
- A megoldásban fel lett használva, hogy dobás után a pénzérme is és a kocka is bármelyik oldalát nem 0 valószínűséggel mutatja, de ez a feladat megfogalmazásában nem szerepelt. Van olyan cinkelt dobókocka, illetve van olyan pénzérme, amely dobás után valamelyik oldalát 0 valószínűséggel mutatja. (Nekem is van olyan dobókockám, amely dobás után garantáltan nem mutat például 2-est vagy 3-ast.) Ellenpélda: p₄=0 és p₅=0 és p₆=0 és q₂=1, p₁=(1−p₂)/2 és p₃=(1−p₂)/2.
- Szinte magától értetődik, de nem az: a megoldás során fel lett használva, hogy a hogy a kocka illetve a pénzérme egymástól függetlenül mutatják valamelyik oldalt. Amennyiben a függetlenség nem teljesül, például a kockában programozható chip és giroszkóp van, és a pénzérmében is is chip és giroszkóp van, akkor ha még dobás után a kocka is bármely oldalát nem 0 valószínűséggel mutatja, és dobás után a pénzérme is bármelyik oldalát nem 0 valószínűséggel mutatja, a programozható chip segítségével elérhető, hogy bizonyos dobások a kockával és a pénzérmével egyszerre ne adódjanak. Mielőtt bárki azt hinné, hogy ez túlzás, van olyan kockám, amelyben chip és giroszkóp van, és lehet telefonnal érzékelni a kocka helyzetét. A pókerversenyeken már a kártyákban is van, hogy chip van, így pókerverseny közvetítésénél a tv-állomás tudja a játékosnál levő lapokat.
Ez a feladat felkeltette az érdeklődésemet, és foglalkoztam a megoldással. Mire végig gondoltam az egész feladatot, hát ezen megfogalmazási pontatlanságok miatt megszenvedtem a megoldással. De így még érdekesebb volt a feladat.
|
| Előzmény: [1171] BerkoErzsebet, 2023-04-13 10:40:16 |
|
| [1171] BerkoErzsebet | 2023-04-13 10:40:16 |
 B. 5306. Igaz, hogy nem életszerű az, hogyha pl. a dobókockával a 2-es dobás valószínűsége 0, de azzal kapcsolatban lenne megjegyzésem, hogy a megoldásnál azt olvasom, hogy hiszen pozitív valószínűséggel dobunk 6 pöttyöt a kockán és 1 pöttyöt az érmén. Dobókocka: p(1)=1, p(2)=p(3)=p(4)=p(5)=p(6)=0; érme: p(1)=1, p(2)=0. Úgy látom, hogy itt 0 valószínűséggel dobunk 6 pöttyöt a kockán és 1 pöttyöt az érmén. Erről a példáról sokat beszélgettem Bertalan Zoltánnal.
B. 5307. A feladatban az van, hogy hegyesszögű háromszögre lássuk be az egyenlőtlenséget, de igaz minden háromszögre. A R=kr helyettesítés nekem sosem jutott volna eszembe.
|
|
| [1170] marcius8 | 2023-03-15 23:23:09 |
 B. 5298
A második elképzelést be lehet fejezni:
Tehát:
tg(Y)=sin(2X)
tg(Z)=sin(2Y)
tg(X)=sin(2Z)
ahol \displaystyle -45°\le X, Y, Z \le+45° érvényes.
Addíciós tétel alkalmazása:
\displaystyle \frac{\sin(Y)}{\cos(Y)}=2\sin(X)\cos(X)
\displaystyle \frac{\sin(Z)}{\cos(Z)}=2\sin(Y)\cos(Y)
\displaystyle \frac{\sin(X)}{\cos(X)}=2\sin(Z)\cos(Z)
Összeszorozva ezt a három egyenletet:
\displaystyle \frac{\sin(Y)\sin(Z)\sin(X)}{\cos(Y)\cos(Z)\cos(X)}=8\sin(X)\sin(Y)\sin(Z)\cos(X)\cos(Y)\cos(Z)
Rendezés, kiemelés:
\displaystyle \sin(Y)\sin(Z)\sin(X)*(8\cos^2(Y)\cos^2(Z)\cos^2(X)-1)=0
Innen:
\displaystyle \sin(Y)\sin(Z)\sin(X)=0 vagy \displaystyle 8\cos^2(Y)\cos^2(Z)\cos^2(X)-1
Figyelembe véve, hogy \displaystyle -45°\le X, Y, Z \le+45°, adódik, hogy csak a korábban felírt triviális megoldások lehetségesek.
|
| Előzmény: [1169] marcius8, 2023-03-15 13:29:03 |
|
| [1169] marcius8 | 2023-03-15 13:29:03 |
 B. 5298. Oldjuk meg a következő egyenletrendszert a valós számok halmazán:
\displaystyle y+yx^2−2x=0 és \displaystyle z+zy^2−2y=0 és \displaystyle x+xz^2−2z=0.
Van több elképzelésem is a feladat megoldásával kapcsolatban.
Rendezve az egyenleteket:
\displaystyle y=\frac{2x}{x^2+1}
\displaystyle z=\frac{2y}{y^2+1}
\displaystyle x=\frac{2z}{z^2+1}
Tekintsük az \displaystyle f(t)=\frac{2t}{t^2+1} függvényt. Ekkor a megoldandó egyenletrendszert a következő alakban lehet írni:
\displaystyle y=f(x) és \displaystyle z=f(y) és \displaystyle x=f(z)
Azaz \displaystyle f(t) olyan függvény, amely \displaystyle x-hez \displaystyle y-t rendeli, \displaystyle y-hez \displaystyle z-t rendeli, \displaystyle z-hez \displaystyle x-t rendeli. Ekkor a következő összefüggések is teljesülnek:
\displaystyle f(f(f(x)))=x és \displaystyle f(f(f(y)))=y és \displaystyle f(f(f(z)))=z
Azaz meg kell keresni azt a \displaystyle t értéket, amelyre teljesül, hogy \displaystyle f(f(f(t)))=t, azaz \displaystyle t fixpontja \displaystyle f\circ f\circ f függvénynek.
Második elképzelés. Legyen \displaystyle x=\tg(X), \displaystyle y=\tg(Y), \displaystyle z=\tg(Z). Ekkor az egyenletek a következőképpen írhatóak:
\displaystyle \tg(Y)=\sin(2X) és \displaystyle \tg(Z)=\sin(2Y) és \displaystyle \tg(X)=\sin(2Y)
És akkor már csak ezt a trigonometrikus egyenletrendszert kellene megoldani.
Az első elképzelésemet nagyjából végigvittem, de a második elképzelésből ki lehetne hozni valamit? Mondjuk az látszik, hogy \displaystyle -45°\le X, Y, Z\le+45°, és a triviális megoldások is látszanak:
\displaystyle X=+45° és \displaystyle Y=+45° és \displaystyle Z=+45°
\displaystyle X=-45° és \displaystyle Y=-45° és \displaystyle Z=-45°
\displaystyle X=0° és \displaystyle Y=0° és \displaystyle Z=0°
|
|
| [1168] Róbert Gida | 2023-02-12 14:27:01 |
 Lejárt A843:
"Modulo \displaystyle q^{e} prímhatvány létezik egy primitív gyök \displaystyle g."
Chat Gpt? Ezt azért ne nagyon reklámozzátok. Itt kell, hogy q nem lehet 2, ami persze teljesül.
|
|
| [1167] Róbert Gida | 2023-01-18 00:00:32 |
 Only for the problem see: A640.
Obviously \displaystyle (p-1)|(n-1) gives a solution (Fermat's little theorem), and using computer found no other solution. It is enough to see: \displaystyle 0<n<p (use again Fermat's little theorem), \displaystyle n is a solution if and only if \displaystyle n+p-1 is a solution. Looks a hard problem.
|
| Előzmény: [1166] Mosi, 2023-01-16 09:00:22 |
|
|
| [1165] Róbert Gida | 2023-01-13 20:25:36 |
 Az azért nagyágyú, amúgy a 3. esetnél is kétszer használták az LTE-t, de a legtriviálisabb \displaystyle v_{2} esetén, itt a konkrét bizonyítás rövidebb lenne, mint az LTE-re való hivatkozás és számolás.
A Beal-sejtéssel is kapcsolatban van a feladat, ami viszont még mindig sejtés. De, ha igaz, akkor a minden kitevő>2 esetet elintézi, mert akkor az alapokat egy prím biztosan osztja, de akkor \displaystyle p=2, ami ellentmondás. Persze igazából nem bizonyít sokat, hiszen nehéz mondjuk \displaystyle b=1,b=2 eseteket bent hagyja.
|
| Előzmény: [1164] Johnny 10, 2023-01-12 20:54:37 |
|
| [1164] Johnny 10 | 2023-01-12 20:54:37 |
 Igen, meg a sok LTE helyett lehet használni Catalan-sejtését (ami most már Mihailescu jóvoltából tétel), hogy az utolsó (és egyben első) szomszédos teljes hatványkból álló a \displaystyle 8-9. Ha ezt használjuk, akkor az egyetlen problémásabb eset az, hogy \displaystyle b páratlan, az összes többit el lehet ezzel intézni.
|
| Előzmény: [1163] Róbert Gida, 2023-01-12 17:15:14 |
|
| [1163] Róbert Gida | 2023-01-12 17:15:14 |
 A frissen lejárt A841.: LTE lemmát sehol nem mondjátok ki.
4. esetnél a kitevőbe került a \displaystyle -1,+1.
És két oldalt levágva a bizonyításból:
2. esetnél: \displaystyle n^2-1=(n-1)(n+1) oszt egy \displaystyle p-hatványt. De akkor \displaystyle n-1,n+1 is \displaystyle p-hatvány. Mivel különségük 2 és p ptlan ez csak úgy lehetséges, hogy \displaystyle n-1=1, azaz \displaystyle n=2, de akkor \displaystyle n+1=3 oszt egy \displaystyle p-hatványt, így \displaystyle p=3. Az egyenlet így: \displaystyle 3^b+1=2^2, így \displaystyle b=1, és itt nincs is több megoldás. LTE lemma nem is kellett.
5. esetnél ugyanez a trükk: \displaystyle 2^a=(n^{\frac{p-1}{2}}+p^h)(n^{\frac{p-1}{2}}-p^h)
A szorzat \displaystyle 2-hatvány, így mindkét tag \displaystyle 2-hatvány, de különbségük \displaystyle 2p^h ami páros, de \displaystyle 4-el nem osztható, mert \displaystyle p páratlan. Ez csak úgy lehetséges, hogy a kisebbik szorzótag \displaystyle 2, innen ugyanaz a bizonyítás.
|
|
| [1162] Lpont | 2022-11-16 12:16:58 |
 A B.5268. feladat egy másik - talán egyszerűbb - megoldása vázlatosan:
Megmutatjuk, hogy P és Q egymás tükörképei az ABC háromszög C-ből induló szögfelezőjére, mint tengelyre.
A. Nyilván, ha P azonos I-vel, akkor CP=CQ triviálisan teljesül, hiszen így a PIQ háromszög egy ponttá fajul.
B. Most különbözzön P I-től és legyen az ABI kör középpontja K.
1. Egyszerű szögszámolással belátható, hogy AKB szög + BCA szög = 180fok, azaz K pont rajta van az ABC háromszög körülírt körén, AKBC négyszög húrnégyszög. Ebben a körben KA=KB, mert ők az ABI kör sugarai, ekkor az ABC körben ezen azonos hosszúságú húrokhoz azonos hosszúságú ívek és egyenlő kerületi szögek tartoznak, tehát KCA szög = KCB szög. Innen kapjuk, hogy K illeszkedik az ABC háromszög C-ből induló szögfelezőjére, vagyis C, I, K pontok kollineárisak.
2. Másrészről Q származtatása miatt az ABI körben PI és QI szakaszok A-ból azonos kerületi szögben látszódnak, tehát PI=QI. Továbbá KP=KQ, mert az ABI kör sugarai, adódik, hogy KPIQ négyszög deltoid, ezért KI átlója merőlegesen felezi a PQ átlóját.
3. Végül C, I, K pontok kollinearitása miatt CK is merőlegesen felezi PQ-t, azaz P és Q egymás tükörképei CK-ra (CI-re), tehát CP=CQ és ezt akartuk bizonyítani.
|
|
| [1161] Lpont | 2022-10-29 08:10:24 |
 Kikerülhető a vektoros megoldás általad említett problémája elemi úton, ha észrevesszük, hogy az AA1, BB1, CC1 szakaszok a párhuzamos szelők tételének megfordítása miatt rendre párhuzamosak és kétszeres hosszúságúak, mint az ABC háromszög C-ből, A-ból és B-ből induló súlyvonalai.
Az pedig jól ismert, hogy a háromszög súlyvonalaiból szerkeszthető háromszög.
|
| Előzmény: [1160] Róbert Gida, 2022-10-29 00:06:43 |
|
|
| [1159] Johnny 10 | 2022-10-27 16:24:49 |
 Vagyis \displaystyle 0 pontosok, jav ...
|
|
| [1158] Johnny 10 | 2022-10-27 16:22:26 |
 A B5255. feladatnál tudja valaki, minek tudható be az \displaystyle 1 pontos dolgozatok szinte irreálisan magas száma (60)?
|
|
| [1157] nadorp | 2022-10-14 20:12:40 |
 Az A.832 feladat központi megoldása szerintem apró hibát tartalmaz. A kérdéses rész a következő:
Legyen \displaystyle t_n annak a valószínűsége, hogy van élő családtag az (n+1)-dik generációban. Ekkor \displaystyle t_n=1−h_n, ahol \displaystyle h_n annak a valószínűsége, hogy 0 gyerek születik az n-edik generációban, ami az n-edik generációhoz tartozó \displaystyle f^{(n)}(x) polinom konstans tagja, azaz \displaystyle h_n=f^{(n)}(0)
Én úgy gondolom, hogy \displaystyle f^{(n)}(0) annak a valószínűsége, hogy 0 egyed van az n-dik generációban. Tehát annak a valószínűsége, hogy 0 gyerek születik az n-edik generációban: \displaystyle h_n=f^{(n+1)}(0).
Innen persze már jó a bizonyítás, mert \displaystyle h_{n+1}=f^{(n+2)}(0)=f(h_n) továbbra is teljesül.
Ha valamit elnéztem, akkor elnézést kérek.
|
|
| [1156] Johnny 10 | 2022-05-14 12:45:43 |
 Illetve végül mégis engedte egy részben...
|
|
| [1155] Johnny 10 | 2022-05-14 12:44:50 |
 Már volt szó a fórumon az A.774. feladatról, most szeretnék én is megosztani egy érdekes megoldást, mely nem teljesen a hagyományos geometriai megoldási módszereken alapszik. A méret korlátja miatt két részben teszem fel.
Megoldásvázlat. (Az állítás egyébként csak hegyesszögű háromszögekre igaz.) Legyen az \displaystyle XYZ háromszög beírt körének középpontja \displaystyle O, a \displaystyle D pont merőleges vetületei az \displaystyle AB, \displaystyle AC és \displaystyle BC egyeneseken rendre \displaystyle T_1, \displaystyle T_2, illetve \displaystyle T_3. Legyen továbbá az \displaystyle ABC háromszög magasságpontja \displaystyle M.
Nagyítsuk az \displaystyle X,Y,Z,O,T_1,T_2,T_3 pontokat kétszeresére \displaystyle D-ből, tetszőleges pont képét egy vesszővel jelöljük. Ekkor \displaystyle X', \displaystyle Y' és \displaystyle Z' az \displaystyle ABC háromszög köréírt körére fognak esni (egy körön lévő pont tükröképei egy átmérőre), míg a \displaystyle T_1T_2T_3 Simson-egyenes jól ismert módon az \displaystyle M ponton átmenő \displaystyle T_1'T_2'T_3' egyenesbe megy át, mely a \displaystyle D pont oldalakra vett tengelyes tükörképeit tartalmazza. Azt kell belátni, hogy \displaystyle O' ezen rajta van.
Vegyük észre, hogy az \displaystyle X'Y'Z' háromszög szögei állandóak, ahogy \displaystyle D mozog a körülírt körön, ugyanis irányított körívekkel számolva \displaystyle \widehat{DX'}=2\widehat{DA}, \displaystyle \widehat{DY'}=2
\widehat, illetve \displaystyle \widehat{DZ'}=2\widehat{DC}, azaz \displaystyle \widehat{X'Y'}=\widehat{DY'}-\widehat{DX'}=2(\widehat{DB}-\widehat{DA}), \displaystyle \widehat{Y'Z'}=2(\widehat{DC}-\widehat{DB}), illetve \displaystyle \widehat{Z'X'}=2(\widehat{DA}-\widehat{DC}), azaz pozitív körüljárási irányban a három pont ugyanolyan helyzetben követi egymást, és akkor az általuk kifeszített háromszög is minden helyzetben egybevágó. Mivel a köréírt köre állandó, ezért ha \displaystyle D egyenletes, egységnyi sebességgel mozog a körön, akkor \displaystyle X'Y'Z' is egységnyi sebességgel forog a köréírt kör középpontja körül. Speciálisan ekkor a háromszög beírt körének középpontja, azaz \displaystyle O is egységnyi sebességgel fog forogni.
Nézzük most a \displaystyle T_1'T_2'T_3' egyenest. Ez megegyezik a \displaystyle T_1'M egyenessel (amennyiben ez a két pont nem esik egybe). \displaystyle T_1' az \displaystyle ABM körön mozog, hiszen jól ismert, hogy ez az \displaystyle ABC kör tengelyes tükörképe az \displaystyle AB egyenesre, ráadásul, ha \displaystyle D egységnyi sebességgel mozog, akkor nyilván a tükörkép is egységnyi sebességgel fog mozogni az \displaystyle ABM körön. A kerületi és középponti szögek tétele alapján ekkor a \displaystyle T_1'T_2'T_3' egyenes \displaystyle \frac12 sebességgel forog \displaystyle M körül. Akár folytonossággal, akár számítással igazolhatjuk, hogy ha \displaystyle T_1' és \displaystyle M egybeesnek, akkor egyenesünk éppen az \displaystyle ABM körhöz \displaystyle M-ben húzott érintő, azaz ebben a helyzetben is igaz, hogy a \displaystyle T_1'T_2'T_3' egyenes fele akkora szöget fordult, mint a \displaystyle D pont (a mozgatás kezdete óta).
Azt kell belátnunk, hogy \displaystyle O mindig rajta van a \displaystyle T_1'T_2'T_3' egyenesen. Vegyük észre, hogy ez biztosan igaz, ha \displaystyle M rajta van azon a körön, amelyen \displaystyle O mozog, ugyanis ekkor fenti megállapításaink szerint \displaystyle O egyszeres sebességgel mozog, míg a \displaystyle T_1'T_2'T_3' egyenes fele sebességgel forog a kör egy pontja körül, és ekkor a kerületi és középponti szögek tétele szerint \displaystyle O mindig rajta lesz az \displaystyle M körül forgó egyenesen.
Ha \displaystyle D éppen egybeesik az \displaystyle ABC háromszög \displaystyle A csúcsával, akkor \displaystyle X', \displaystyle T_1' és \displaystyle T_2' is egybeesnek az \displaystyle A ponttal, azaz a \displaystyle T_1'T_2'T_3' egyenes éppen az \displaystyle A-ból \displaystyle BC-re állított merőleges (hiszen az \displaystyle AT_3' egyenes a tükrözés miatt merőleges \displaystyle BC-re). Másrészt némi szögszámolással (felhasználva, hogy \displaystyle BY'=BX'\equiv{BA} és \displaystyle CZ'=CX'\equiv{CA}, hiszen \displaystyle Y', illetve \displaystyle Z' a \displaystyle D\equiv{X} pont \displaystyle BO-ra, illetve \displaystyle CO-ra vonatkozó tükörképei) könnyen belátható, hogy amennyiben \displaystyle ABC hegyesszögű, akkor az \displaystyle A-ból induló magasság, mely a \displaystyle T_1'T_2'T_3' egyenes jelen helyzetben, felezi az \displaystyle Y'X'Z' szöget, mégpedig belső szögfelező (azért nem írom ezt le részletesebben, mert a teljesség igényével itt több különböző esetet kell megvizsgálni a pontok elhelyezkedése szerint, irányított szögekkel csak részben kerülhető el a diszkusszió, azt be kell látni, hogy a kapott szögfelező belső szögfelező, ld. például a tompaszögűek esetén nem az). Így a \displaystyle T_1'T_2'T_3' egyenesen ebben az esetben rajta van \displaystyle O. Hasonlóképp \displaystyle O akkor is rajta van a \displaystyle T_1'T_2'T_3' egyenesen, ha \displaystyle D a háromszög \displaystyle B csúcsával esik egybe. Belátjuk, hogy ez csak úgy lehet, hogy \displaystyle M rajta van az \displaystyle O által befutott körön.
Ugyanis mozgatásunknál megállapítottak alapján \displaystyle O a két helyzet között kétszer akkora szöget tett meg, mint amennyit a \displaystyle T_1'T_2'T_3' egyenes \displaystyle M körül elfordult. Így ha mindkétszer (jelöljük ezeket a helyeket \displaystyle O_1-gyel és \displaystyle O_2-vel) rajta van az egyenesen, akkor irányított szögekkel \displaystyle \angle{(MO_1,MO_2)} éppen kétszer akkora, mint az \displaystyle O lehetséges helyzetei által alkotott körön vett \displaystyle \widehat{O_1O_2} irányított ívhez tartozó kerületi szög. Így a kerületi és középponti szögek tételének megfordítása miatt \displaystyle M rajta van az \displaystyle O által befutott körön, és a fentiek szerint ebből már adódik az állítás.
Végül pedig visszakicsinyítve a pontokat azt kapjuk, hogy \displaystyle T_1T_2T_3O is kollineáris, és ezt akartuk belátni.
U.i.: Tompaszögű háromszög esetén módosítani kell kicsit az állításon: ekkor a tompaszöggel szemközti hozzáírt kör középponta van rajta a \displaystyle D-hez tartozó Simson-egyenesen.
|
|
| [1154] marcius8 | 2022-05-03 17:04:00 |
 B. 5233. feladat: Ekkor mennyi lehet a hatszög két (szemközti, szomszédos) oldalára írt szám korrelációs együtthatója?
B. 5233. Egy szabályos hatszög csúcsaira véletlenszerű sorrendben felírjuk az 1,2,…,6 számokat. Ezután a hatszög minden oldalára ráírjuk a két végpontján szereplő számok különbségének abszolútértékét. Határozzuk meg az oldalakra írt hat szám összegének várható értékét.
|
|
| [1153] Róbert Gida | 2022-04-13 18:05:27 |
 Lejárt A822. feladatnál a közölt megoldáshoz képest a változók felét lehet megspórolni, és sokkal jobban is látható a bizonyítás:
Feltehetö \displaystyle p=\frac an,q=\frac bn,r=\frac cn ekkor \displaystyle a+b+c=0 és \displaystyle a*b*c=n^3 azaz: \displaystyle a*b*(a+b)=-n^3
legyen lnko(a,b)=g, ekkor \displaystyle a=g*u,b=g*v és itt már lnko(\displaystyle u,v)=\displaystyle 1, itt \displaystyle a,b értékét beírva kapjuk:
\displaystyle g^3*u*v*(u+v)=-n^3
azaz \displaystyle u*v*(u+v)=d^3 ahol \displaystyle d=-\frac ng-nek egésznek kell lennie. Triviálisan u,v,u+v páronként relatív prím.
Így a szorzat minden tagja köbszám: \displaystyle u=x^3,v=y^3,u+v=z^3 és így: \displaystyle x^3+y^3=z^3 valamely \displaystyle x,y,z nemnulla egészekre ami a Fermat egyenlet spec esete, nincs megoldása.
|
|
| [1152] Róbert Gida | 2022-01-16 22:21:26 |
 Lejárt A812. megoldása pongyola, hiányzik a bizonyításból, hogy teljes indukciót alkalmazunk, például az \displaystyle n+k összegre.
|
|
| [1151] marcius8 | 2021-12-19 21:55:00 |
 Eredeti megfogalmazásomban a következőképpen nézett ki az előbb felvetett probléma, amelyet Kós Géza Tanár Úr átfogalmazott, és a KöMaL-pontversenybe került be: (érdekes matek feladatok, [3668])
Egy játékot találtam ki. Mivel egy játékkal akkor foglalkoznak sokan, ha szabályai egyszerűek, ugyanakkor nem könnyen végigjátszható, ezért a következő játékot találtam ki:
A magyar kártyacsomag összetétele: A magyar kártyacsomag 32 lapot tartalmaz. Minden lapnak van színe és értéke. A színek lehetnek: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél). Az értékek lehetnek: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”. A kártyacsomagban minden lehetséges szín-érték párosítás előfordul.
A nyolc sorból és négy oszlopból álló táblázatban elhelyezett magyar kártyacsomag lapjai akkor vannak rendezett sorrendben, ha a következő feltételek teljesülnek:
• A táblázat minden oszlopában található négy lap színének sorrendje felülről lefelé haladva: „piros” (tavasz), „tök” (nyár), „zöld” (ősz), „makk” (tél).
• A táblázat minden sorában található nyolc lap értékének sorrendje balról jobbra haladva: „VII”, „VIII”, „IX”, „X”, „alsó”, „felső”, „király”, „ász”.
A játék szabálya: A kártyacsomag lapjai véletlenszerű sorrendben egy négy sorból és nyolc oszlopból álló táblázatban vannak elhelyezve. A játék során egyszerre mindig két lapot lehet megcserélni. Két lapot csak akkor lehet megcserélni, ha a két lap ugyanabban a sorban vagy ugyanabban az oszlopban van, továbbá (és) ha a két lap színe vagy értéke ugyanaz. A játék célja, hogy a kártyalapok sorrendje rendezett legyen.
Az érdekes az hogy a véletlenszerűen összekevert állapotból majdnem mindig abba az állapotba jutok, hogy a rendezett állapothoz képest a "makk ász" és a "tök király" fel van cserélve. Sajnos, nem tudok rájönni, hogy ez az én ügyetlenségem (gyanítom, hogy igen), de ugyanakkor nem hiszem hogy ennek törvényszerűen így kell lenni. Arra kérek bárkit, hogy ha ezt a jelenséget meg tudja indokolni, vagy meg tudja oldani (tehát ha a rendezett állapothoz képest csak a "makk ász" és a "tök király" van felcserélve, akkor ez az állapot rendezhető vagy sem), írjon a marcius.08@freemail.hu címre.
|
| Előzmény: [1150] marcius8, 2021-12-19 16:06:09 |
|
| [1150] marcius8 | 2021-12-19 16:06:09 |
 A következő feladat megoldását keresem. Annak idején ezt a problémát én vetettem fel a fórumban, de akkor sem tudtam a megoldását, egy passziánsz játékot terveztem számítógépre, Kós Géza Tanár Úr tette be a kömal-pontversenybe. Ha valaki el tudná küldeni ennek a feladatnak a megoldását, nagyon megköszönöm. A feladatot kicsit átfogalmaztam annyiban, hogy más betűjeleket használok, illetve egy kérdést hozzátettem.
A. 585. (2013 március) Adottak az \displaystyle i_0\ge2, \displaystyle j_0\ge2 egész számok. Az \displaystyle (i,j) számpárokat, ahol \displaystyle 1\le{i}\le{i_0}, \displaystyle 1\le{j}\le{j_0} egészek, ráírtuk egy-egy kártyára úgy, hogy mindegyik pár pontosan egy kártyán szerepeljen. Ezután a következő játékot játsszuk: Az \displaystyle i_0*j_0 darab kártyát elhelyezzük egy \displaystyle i_0×j_0-ás táblázatban úgy, hogy minden \displaystyle i-re és \displaystyle j-re az \displaystyle (i,j) kártya az \displaystyle i-edik sorban és a \displaystyle j-edik oszlopban legyen, tekintsük ezt az elrendezést természetesnek. Az \displaystyle (i_1,j_1) és \displaystyle (i_2,j_2) kártyákat felcserélhetjük, ha ugyanabban a sorban vagy ugyanabban az oszlopban vannak, és \displaystyle i_1=i_2 vagy \displaystyle j_1=j_2.
Elérhetjük-e ilyen lépésekkel, hogy pontosan két kártya helyet cseréljen, a többi kártya pedig visszakerüljön a kiinduló helyére? És mi annak a szükséges és elégséges feltétele, hogy egy \displaystyle i_0×j_0-ás táblázatban tetszőlegen elhelyezett kártyákat a megengedett felcserélésekkel természetes sorrendbe lehet rendezni?
|
|
| [1149] Tashi | 2021-11-11 11:59:17 |
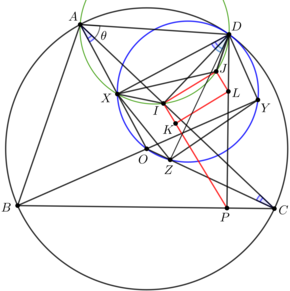
 I post my solution to the problem A. 774 because it shows that the problem is one of the few applications of the Japanese theorem.
Let \displaystyle I be the projection of the point \displaystyle D on the line \displaystyle AC.
Let \displaystyle J, \displaystyle K and \displaystyle L, respectively be the incenters of the triangles \displaystyle \Delta XDY, \displaystyle \Delta XYZ and \displaystyle \Delta DYZ, respectively.
From \displaystyle DX\perp AO,\; DY\perp BO,\; DZ \perp CO it follows that
\displaystyle D,O,X,Y,Z\text{ lies on the circle of diameter } DO\tag{1}
Let \displaystyle P be the projection of \displaystyle D on the line \displaystyle BC, \displaystyle A=\measuredangle
BAC and similarly we define \displaystyle B and \displaystyle C, let \displaystyle \theta=\measuredangle
DAC.
From \displaystyle (1) it follows that \displaystyle \measuredangle XDI=\measuredangle OAC=\measuredangle
OCA=\measuredangle ZDI\Rightarrow
\displaystyle \measuredangle XDI=\measuredangle ZDI\tag{2}
From \displaystyle (1) it follows that \displaystyle \measuredangle DXZ=180^\circ- \measuredangle
DOZ=\measuredangle DOC=2\measuredangle CAD=\measuredangle DXI, which implies \displaystyle \measuredangle DXI=\measuredangle ZXI. From this and \displaystyle (2) it follows that
\displaystyle I\text{ is the incenter of the triangle } XDZ\tag{3}
From \displaystyle (1) it follows that
\displaystyle \measuredangle XDJ=\frac12\measuredangle
XDY=\frac12(180^\circ-\measuredangle XOY)=\frac12\measuredangle AOB
=C.
But from \displaystyle \measuredangle ADI=90^\circ-\theta it follows that \displaystyle \measuredangle ADX=90^\circ-\theta-(90^\circ-B)=B-\theta. From this and \displaystyle \measuredangle ADJ=\measuredangle ADX+\measuredangle XDJ it follows that
\displaystyle \measuredangle ADJ=B-\theta+\measuredangle XDJ{=}
B+C-\theta=180^\circ-A-\theta\tag{4}
From \displaystyle (3) it follows that
\displaystyle \measuredangle XUD=90^\circ + \frac12\measuredangle XZD=90^\circ +
\frac12\measuredangle XYD=\measuredangle XJD,
which implies that the quadrilateral \displaystyle XIJD is cyclic. From this and \displaystyle (1) it follows that the points \displaystyle X,I,J,A,D are concyclic, which implies \displaystyle \measuredangle AIJ=180^\circ-\measuredangle ADJ. From this and \displaystyle (4) it follows that \displaystyle \measuredangle AIJ=A+\theta=\measuredangle BAD.
From this and \displaystyle (1) it follows that
\displaystyle
\measuredangle PIC=\measuredangle PDC=90^\circ-\measuredangle
DCP=90^\circ-(180^\circ-\measuredangle
BAD)=\measuredangle BAD-90^\circ
\displaystyle =\measuredangle AIJ-90^\circ=\measuredangle AIJ-\measuredangle
DIA=\measuredangle DIJ,
which implies
\displaystyle \measuredangle PIJ= \measuredangle PIC+\measuredangle
CIJ=\measuredangle DIJ+\measuredangle CIJ=\measuredangle
CID=90^\circ\tag{5}
From \displaystyle (1), \displaystyle (3) and the Japanese theorem in \displaystyle DXYZ it follows that \displaystyle IJKL is rectangle, which implies \displaystyle \measuredangle
KIJ=90^\circ. From this and \displaystyle (5) it follows that \displaystyle K\in PI, which is the \displaystyle P-Simson line in \displaystyle \Delta ABC. Thus, we have solved the problem.
|
 |
|






