| [163] sakkmath | 2006-01-31 14:08:59 |
 Kedves Fórumosok! Az Euklides 2.41-es verziójában találtam egy hibát. A honlapjukon megadott címekre 5 hete e-mailben elküldtem a hibaleírást, de nem válaszolnak. A honlapon mellesleg ez a lehangoló infó olvasható: utolsó frissítés: 2002. január 27. Ismeri-e valaki a szerzők/fejlesztők elérhetőségeit?
|
|
|
| [161] V Laci | 2006-01-29 13:12:00 |
 Tényleg szép megoldás, köszönöm szépen!
|
|
|
|
| [158] V Laci | 2006-01-28 17:54:38 |
 Sziasztok!
Érdekelne a B.3853. feladat megoldása. (Háromszög területét felező adott irányú egyenes szerkesztése.) Előre is köszönöm.
Iván88, nekem van egy megoldásom a B.3859. feladatra, sztem jó, de ez nem biztos :), de ha gondolod szívesen elküldöm e-mailben.
|
|
| [157] Iván88 | 2006-01-27 21:50:18 |
 Valaki írja meg a B. 3859-esnek a megoldását! Ne hagyjuk félbe! (Addig nem nyugszom, amíg nem lesz fenn)
|
|
|
|
| [154] Lóczi Lajos | 2006-01-22 18:04:48 |
 A 2x=x2 egyenlet egyetlen negatív valós gyökét nemelemi függvényekkel fel lehet írni, pl. az ún. Lambert-féle W-függvénnyel, de ezzel a felírással nem mennél túl sokra, mert benne az x xex függvényt kell invertálni. Az inverz (alkalmas intervallumon) létezik, de "képlettel" (azaz véges sok elemi függvény segítségével) nem írható fel. A transzcendens egyenletek szinte mindig ilyenek, ezen nem kell csodálkozni. xex függvényt kell invertálni. Az inverz (alkalmas intervallumon) létezik, de "képlettel" (azaz véges sok elemi függvény segítségével) nem írható fel. A transzcendens egyenletek szinte mindig ilyenek, ezen nem kell csodálkozni.
Numerikusan tetszőleges pontossággal megközelíthető a gyök: az első néhány tizedesjegy -0.7666646... A határérték fogalmával szintén könnyedén kifejezhető ez a szám: tekintsük pl. az
x0=1,  rekurziót. Ekkor rekurziót. Ekkor 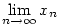 adja a keresett negatív megoldást. adja a keresett negatív megoldást.
|
| Előzmény: [146] ScarMan, 2006-01-21 13:15:29 |
|
| [153] Lóczi Lajos | 2006-01-22 17:42:00 |
 Az Általad említett x=(1+1/n)n, y=(1+1/n)n+1 (vagy fordítottja) formula (n pozitív egész) a pozitív racionális megoldásokra vonatkozik -- itt egyik feltétel sem teljesül.
(Amúgy azóta a TMCS folyóirat 2003-as számában megjelentek a negatív valós, negatív racionális, illetve komplex megoldásokra vonatkozó eredmények is.)
|
| Előzmény: [147] rizsesz, 2006-01-21 16:10:56 |
|
| [152] lorantfy | 2006-01-22 15:35:30 |
 Di-Lemma: Először azt kellene belátnunk, hogy a sakktábla fekete mezőire helyezett k<32 db ló, mindig k-nál több különböző fehér mezőre üt.
Ha ez igaz, akkor tekintsük a világos mezőkön álló 32 ló elhelyezést.
Tfh. létezik olyan, a feladatnak megfelelő elhelyezés ahol k<32 ló sötét mezőn áll. Akkor ez az elrendezés elérhető úgy, hogy a 32 világos helyről k db lovat sötét mezőre helyezünk. De ezek k-nál több különböző fehér mezőre ütnek, tehát nem ütheti csak a megüresedett k helyet. Ellentmondás.
Márcsak a Di-lemmát kell bizonyítani!
|
| Előzmény: [151] Káli gúla, 2006-01-22 14:34:17 |
|
|
| [150] jonas | 2006-01-22 13:19:17 |
 Ez szép megoldás.
Szerintem viszont nem kell tudni, hogy a sakktáblán lehet teljes kört megtenni (ami persze ismert, de ha valaki nem ismeri, akkor nem könnyű belátni). Elég, ha egy 1-faktort megadunk, vagyis párosítjuk a mezőket úgy, hogy minden pár két mezője támadja egymást. Ilyet pedig egyszerű mutatni, például
és még hét ugyanilyen példány.
|
| Előzmény: [145] ScarMan, 2006-01-21 12:10:33 |
|
| [149] lorantfy | 2006-01-22 10:45:59 |
 Kedves Fórumosok!
Kaptam egy levelet Bodnár Jánostól, aki B. 3869. feladatot javasolta, és azt kéri tőletek, hogy akinek van kedve hozzá, próbálja megoldani a feladatot inverzió segítségével vagy pont körre vonatkozó hatványát felhasználva!
Ha valaki esetleg ilyen megoldást köldött be, jó lenne, ha megosztaná velünk!
|
|
| [148] lorantfy | 2006-01-21 21:24:44 |
 Szia Rizsesz!
Lóczi Lajos cikkében a hatványozás kommutativitásának lehetőségét keresi, az xy=yx egyenlet megoldásait.
Alapfeltevés, hogy x,y pozitív valós számok!
Nóra itt most a 2x=x2 egyenlet egy negatív megoldását szeretné megtalálni. Szerintem ezt nem lehet 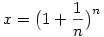 alakban felírni. alakban felírni.
|
| Előzmény: [147] rizsesz, 2006-01-21 16:10:56 |
|
| [147] rizsesz | 2006-01-21 16:10:56 |
 Lóczi Lajos 2000. januárjában megjelent cikke szerint azt hiszem az a ad b=b ad a egyenlet gyökei a=(1+1/n) ad n és b=(1+1/n) ad (n+1) (TeX :)), illetve az a=b eset. ebből származtatható a 2 megoldás.
|
|
| [146] ScarMan | 2006-01-21 13:15:29 |
 A B.3871. feladathoz:
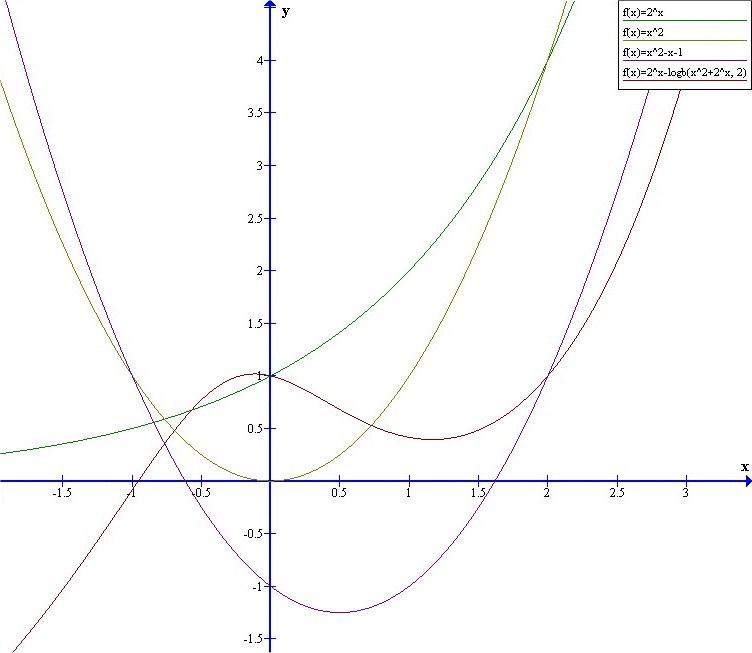
Ha ábrázoljuk koordinátarendszerben az eredeti egyneletet (lila és barna vonal metszéspontjai) és a 2x=x2 egyenletet (zöld és sárga vonal metszéspontjai), látszik, hogy ugyanazok a megoldásiak. Pozitív számok esetén a két gyök 2 és 4, ezek egész számok, így behelyettesítéssel könnyen bizonyítható, hogy ez a kettő a megoldás. De van a negatív számok halmazán is egy megoldás, x3=-0,76 környékén. Hogy lehetne megoldani a 2x=x2 egyenletet, hogy ezt a gyököt is megkapjuk? Nincs valakinek ötlete?
|
 |
| Előzmény: [139] Iván88, 2006-01-19 19:50:59 |
|
| [145] ScarMan | 2006-01-21 12:10:33 |
 Beírok egy feladatot én is, elnézést, ha kicsit kacifántosan írtam le (ha vmit rosszul akkor pláne), de nem kellett bele TeX, és legalább népszerűsödik a téma.
B.3862. feladat megoldása:
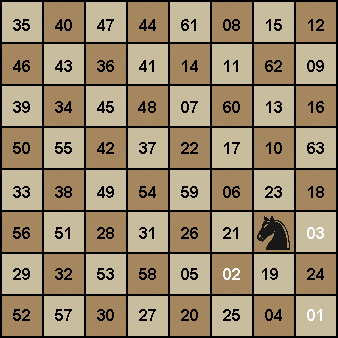
Ismeretes, hogy a sakktáblán végig lehet úgy léptetni egy huszárt, hogy az minden mezőre pontosan egyszer lép rá, és az utolsó mezőről visszatérhet a kezdő mezőre (ld. ábra). Egy ilyen út látható az ábrán. Ez az út 64 lépésből áll, hiszen ennyi a mezők száma. Ha el akarunk helyezni 32 huszárt a mezőkön úgy, hogy azok ne támadják egymást, nem tehetünk két huszárt két, az út során egymást követő mezőre.
Ez azt jelenti, hogy az 1-64 számokból kell kiválasztanunk 32-őt, úgy, hogy semelyik kettő ne legyen szomszédos, és itt a 64-et és az 1-et is szomszédosnak tekintjük. Ezt csak úgy tehetjük meg, ha minden második számot választunk ki. Legalább egy szám ugyanis mindenképp kell legyen két szám között, tehát minden szám után kell hagynunk egy helyet, vagyis egy szám legalább két helyet foglal, így a 32 kiválasztott szám összesen lefoglalja mind a 64-et, ez a legjobb eset, amikor mindenhol egy szám marad ki. Sehol sem marad ki egy számnál több, így ha valahol többet hagynánk ki, a maradékot már nem tudnánk megfelelően elhelyezni.
Minden második számot kétféleképpen tudjuk kiválasztani: vagy a páros számokat, vagy a páratlan számokat. Látható, hogy a huszár mindig a saját mezőjével ellentétes színű mezőt támad, tehát egyrészt az azonos színű mezők nem támadhatják egymást, másrészt a huszár által bejárt út a sakktáblán váltakozó színű mezőkön történik, tehát az azonos paritású lépések azonos, a különböző paritású lépések különböző színűek.
Ez azt jelenti, hogy a két lehetséges kiválasztás: minden fehér, vagy minden fekete mezőre állítunk egy huszárt. Így ezek a huszárok valóban nem fogják egymást támadni, hiszen megegyező színű mezőn állnak.
|
 |
|
| [144] lorantfy | 2006-01-21 00:03:53 |
 Mert a log2(x) fgv. szig. mon. növekvő, tehát nagyobb szám logaritmusa nagyobb.
Így pl. ha x2<2x akkor x2 helyett 2x-t írva a fgv. "hasába" nagyobb értéket kapunk:
x2+log2(x2+2x)<x2+log2(2x+2x)=x2+log2(2x+1)=x2+x+1<2x+x+1
Vagyis x2+log2(x2+2x)<2x+x+1, nem lehet egyenlőség.
És fordítva, ha x2>2x, akkor:
x2+log2(x2+2x)>x2+log2(2x+2x)=x2+log2(2x+1)=x2+x+1>2x+x+1
Tehát x2+log2(x2+2x)>2x+x+1, így sem lehet egyenlőség.
Éppen azt láttuk be, hogy egyenlőség akkor, és csak akkor lehet, ha x2=2x.
Erre jutottál Te is, csak a végén az a "más megoldás nincs" kijelentés nem elég meggyőző.
|
| Előzmény: [143] Iván88, 2006-01-20 22:16:57 |
|
|
| [142] lorantfy | 2006-01-19 22:37:54 |
 Szia Iván!
Megvizsgáltad az x2 és a 2x viszonyát x különböző értékeinél, most azt kéne megnézni, hogyan változik a log2(x2+2x) értéke ha x2 helyett 2x-t írsz bele! Közben a másik oldalon 2x helyett x2-t írunk!
Melyik intervallumon, hogyan változik a két oldal értéke?
|
| Előzmény: [139] Iván88, 2006-01-19 19:50:59 |
|
|
|
| [139] Iván88 | 2006-01-19 19:50:59 |
 Valaki monja meg, hogy hogyan kell megoldani(teljesen) a B. 3859-est!
Addig is elküldöm a B. 3871-esre az én megoldásomat.
B. 3871. Oldjuk meg az
x2-x-1=2x-log2(x2+2x)
egyenletet a pozitív számok körében.
Itt aztán minden van. Hatványtag, exponenciális tag és logaritmikus tag is. Nem éri meg kibontani őket. Néhány számot próbáljunk ki, hátha lesz valami. Így kapjuk azt hogy a 2 és a 4 megoldásai az egyenletnek. Megmutatjuk, hogy más megoldás nincsen.
Az én ötletem az volt, hogy (mivel az x2+2x szerepel a logaritmus után és az egyenlet mindkét oldalán (egyiken az egyyik, másikon a másik)) hasonlítrsuk össze az x2-et a 2x-nel. A két függvényt ábrázolva azt kapjuk, hogy x2=2x, ha x1;2=2; 4; x·2>2x, ha 2<x<4 , minden egyéb esetben 2x>x2, mivel 0<x.
Nézzük meg, hogy milyen relációkapcsolatban van x+1, a log2(x2+2x)-nel. Néhány ekvivalens átrendezés után azt kapjuk, hogy az x+1-ből 2x, a log2(x2+2x)-ből az x2-es tag "keletkezik".
Az eredeti egyenletet az alábbi alakra hozva azt kapjuk, hogy:
x2+log2(x2+2x)=2x+x+1
a bal oldalon állnak az "x2-es tagok" (reláció szempontjából), míg a jobb oldalon a "2x-esek". Mivel x2=2x, ha x1;2=2; 4, így más megoldás nincs.
|
|








 xex függvényt kell invertálni. Az inverz (alkalmas intervallumon) létezik, de "képlettel" (azaz véges sok elemi függvény segítségével) nem írható fel. A transzcendens egyenletek szinte mindig ilyenek, ezen nem kell csodálkozni.
xex függvényt kell invertálni. Az inverz (alkalmas intervallumon) létezik, de "képlettel" (azaz véges sok elemi függvény segítségével) nem írható fel. A transzcendens egyenletek szinte mindig ilyenek, ezen nem kell csodálkozni. 




 hasonló AB2C2
hasonló AB2C2 c1 és b2=
c1 és b2= =
= +
+ =B1AB2
=B1AB2 AC1C2
AC1C2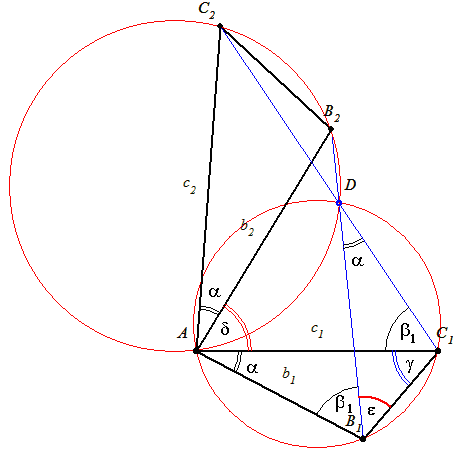
 1=AC1C2
1=AC1C2 és
és  mindkettőben közös, így B1DC1
mindkettőben közös, így B1DC1