Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[170] HoA	2006-02-27 17:26:51
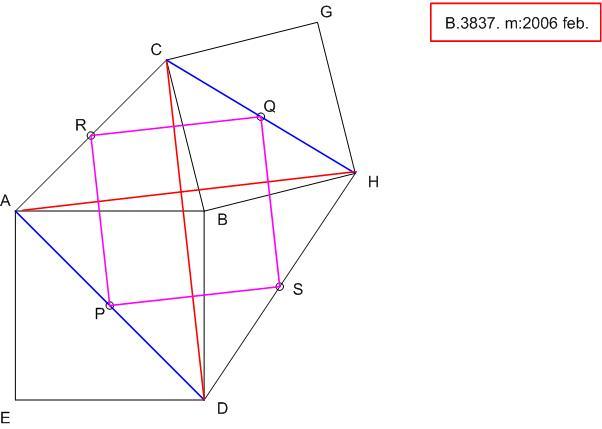
Kedves Fórumosok! Most jelentek meg (2006. február) a B. 3837. megoldásai, szeretnék mutatni rá egy elemi megoldást. Használjuk fel azt a tételt, hogy egy N₁ négyszög oldalfelező pontjai által meghatározott N₂ négyszög paralelogramma, mert szemközti oldalai párhuzamosak N₁ egyik átlójával és fele olyan hosszúak, mint az N₁ -átló. Ebből az is következik, hogy ha N₁ átlói egyenlőek és merőlegesek egymásra, akkor N₂ szomszédos oldalai is egyenlőek és merőlegesek egymásra, tehát N₂ négyzet. Feladatunkban P, S, Q, R az ADHC négyszög oldalfelező pontjai, ezért csak azt kell megmutatnunk, hogy AH és DC egyenlőek és merőlegesek egymásra. Forgassuk el az ABH $\Delta$ -et B körül 90^o -kal pozitív irányban. Ekkor A D-be, H C-be kerül, AH elforgatottja DC lesz, ezért AH és DC valóban egyenlőek és merőlegesek egymásra.

Előzmény: [99] lorantfy, 2005-10-18 18:36:36

[169] Doom	2006-02-19 13:44:04
Szép megoldás, nekem tetszik! :)
Előzmény: [168] [evilcman], 2006-02-18 22:16:05

[168] [evilcman]	2006-02-18 22:16:05
Töltöttem fel egy megoldást a B.3881.-es feladatra: http://thevilcman.atw.hu/files.html Szerintem jó :) Viszont elég hosszadalmas.

[167] lorantfy

2006-02-18 16:21:38

B. 3877. feladat megoldása: Az S pont az FC súlyvonalat harmadolja. PFS $\Delta$ és QCS $\Delta$ hasonló - mert két oldalegyenesük közös és PF párhuzamos CQ - és a hasonlóság aránya 1:2.

Legyen AB=c, PF=x, ekkor CQ= 2x. Az R ponton átmenő AB-re merőleges egyenes AB-vel és CQ-val való metszéspontjai legyenek M és N pontok. MN=m, az ABC $\Delta$ magassága.

ABR $\Delta$ hasonló QCR $\Delta$ , mert két oldalegyenesük közös és AB párhuzamos CQ és a hasonlóság aránya:

$\lambda = \frac{AB}{CQ}= \frac{c}{2x}$ Így arányos osztással: $MR= \frac {mc}{c+2x}$ . Látszik, hogy $PB= \frac{c}{2}+x$

A PBR $\Delta$ területe: $T_1=\frac {1}{2} PB \cdot MR= \frac {1}{2} (\frac{c}{2}+x) \frac {mc}{c+2x}=\frac {1}{4}(c+2x) \frac {mc}{c+2x}=\frac {1}{4}mc=\frac{T_{\Delta} }{2}$

Tehát PR szakasz felezi az ABC $\Delta$ területét.

[166] Káli gúla	2006-02-08 15:51:48
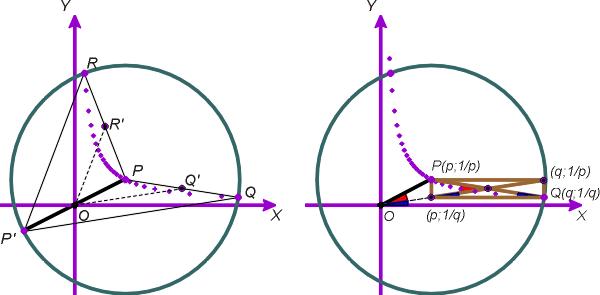
Ha elfogadjuk, hogy a PQ felezőpontját az origóval összekötő OQ' egyenes harmadolja a POX szöget, akkor R'OQ' szög az YOX derékszög kétharmada, tehát 60^o-os. A párhuzamos szárak miatt a RP'Q szög is ugyanekkora, ezért a RQ-hoz tartozó RPQ középponti szög 120^o-os. Húzzunk a P és Q pontokon át párhuzamosokat a tengelyekkel. A kapott (barna) téglalapban az átlók szöge (piros) külső szög, ezért kétszer akkora, mint az átlóknak a vízszintes oldallal bezárt szöge (kék). A két piros szög azért egyenlő, mert egyrészt a feltétel szerint OP=PQ/2, másrészt a (q;1/p) és a (p;1/q) pontokat összekötő átló meghosszabbítása átmegy az origón. Tehát az O pontnál a piros szög valóban kétszer akkora, mint a kék. Ez a szép és lényegében semmilyen előismeretet nem igénylő bizonyítás a P. 27-es, pontversenyen kívüli feladat hivatalos megoldása volt 1969-ben: ld. archívum.

Előzmény: [165] HoA, 2006-02-07 17:27:30

[165] HoA

2006-02-07 17:27:30

Kedves Fórumosok!

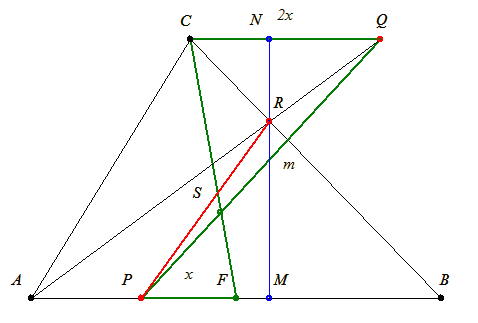
Az A. 386. feladathoz javaslok egy - szerintem - a honlapon megjelentnél sokkal egyszerűbb megoldást. Használjuk a honlap ábráját. Legyen az OP vektor hossza t, irányszöge $\alpha$ . Ekkor P koordinátái (t cos $\alpha$ ; t sin $\alpha$ ). Mivel P a hiperbolán van, ennek egyenlete

xy=t²cos $\alpha$ sin $\alpha$

A P-ből a kör/hiperbola metszéspontok egyikébe, mondjuk T-be mutató 2t hosszúságú PT vektor irányszöge legyen $\beta$ , ekkor T koordinátái

(t cos $\alpha$ +2t cos $\beta$ ; t sin $\alpha$ +2t sin $\beta$ )

T is a hiperbolán van, ezért

(t cos $\alpha$ +2t cos $\beta$ )(t sin $\alpha$ +2t sin $\beta$ )=t²cos $\alpha$ sin $\alpha$

t²(cos $\alpha$ sin $\alpha$ +2 cos $\beta$ sin $\alpha$ +2 cos $\alpha$ sin $\beta$ +4 cos $\beta$ sin $\beta$ )=t²cos $\alpha$ sin $\alpha$

2 cos $\beta$ sin $\alpha$ +2 cos $\alpha$ sin $\beta$ +4 cos $\beta$ sin $\beta$ =0

sin( $\alpha$ + $\beta$ )= -sin(2 $\beta$ )=sin(-2 $\beta$ )

Felhasználva, hogy sin x=sin( $\pi$ -x) , innen vagy

(a)	$\alpha$ + $\beta$ = -2 $\beta$ +2k $\pi$

, vagy pedig

(b)	$\alpha$ + $\beta$ = $\pi$ +2 $\beta$ +2k $\pi$

A (b) esetben

$\beta$ = $\alpha$ -(2k+1) $\pi$

, vagyis a PT irány éppen OP-vel ellentétes, ez a metszéspont ábránk P' pontja. Az (a) esetben

3 $\beta$ = - $\alpha$ +2k $\pi$

$\beta = ~-\frac\alpha3 + k \frac{2\pi}3$

vagyis a P-ből a kör/hiperbola metszéspontokba mutató vektorok egymás 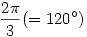$\frac{2\pi}3 (=120^\circ)$ egész számú többszöröseivel való elforgatottjai, az ábra PQ, PR és PS vektorai. Közülük bármely kettő, így a PQ és PR által bezárt szög is 120^o A megoldás a hivatkozott szögharmadolásra is rámutat: utolsó képletünkben k = 0 -t véve

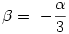
$\beta = ~-\frac\alpha3$

, tehát a megoldás vektorok egyikének ( ábránkon PQ ) irányszöge abszolút értékre megegyezik az OP vektor irányszögének harmadával.

[164] Iván88

2006-02-06 19:35:43

Akkor légyszi írd meg.

<ivan9d@freemail.hu>

Köszi: Gresits Iván

Előzmény: [158] V Laci, 2006-01-28 17:54:38

[163] sakkmath	2006-01-31 14:08:59
Kedves Fórumosok! Az Euklides 2.41-es verziójában találtam egy hibát. A honlapjukon megadott címekre 5 hete e-mailben elküldtem a hibaleírást, de nem válaszolnak. A honlapon mellesleg ez a lehangoló infó olvasható: utolsó frissítés: 2002. január 27. Ismeri-e valaki a szerzők/fejlesztők elérhetőségeit?

[162] [evilcman]

2006-01-31 13:15:59

Köszönöm!

Euklides-t használok.

Előzmény: [160] lorantfy, 2006-01-29 10:15:16

[161] V Laci	2006-01-29 13:12:00
Tényleg szép megoldás, köszönöm szépen!

[160] lorantfy	2006-01-29 10:15:16
Szép megoldás! Gratula! Milyen szerkesztő programot használsz?
Előzmény: [159] [evilcman], 2006-01-29 00:55:49

[159] [evilcman]	2006-01-29 00:55:49
Itt egy: http://users.atw.hu/thevilcman/files.html
Előzmény: [158] V Laci, 2006-01-28 17:54:38

[158] V Laci

2006-01-28 17:54:38

Sziasztok!

Érdekelne a B.3853. feladat megoldása. (Háromszög területét felező adott irányú egyenes szerkesztése.) Előre is köszönöm.

Iván88, nekem van egy megoldásom a B.3859. feladatra, sztem jó, de ez nem biztos :), de ha gondolod szívesen elküldöm e-mailben.

[157] Iván88	2006-01-27 21:50:18
Valaki írja meg a B. 3859-esnek a megoldását! Ne hagyjuk félbe! (Addig nem nyugszom, amíg nem lesz fenn)

[156] Lóczi Lajos	2006-01-22 18:11:15
Amúgy hasonló (de szerintem jóval nehezebb) kérdést feszeget a Nehezebb mat. probl. 136. feladatában kitűzött egyenlőtlenség is.
Előzmény: [146] ScarMan, 2006-01-21 13:15:29

[155] Lóczi Lajos	2006-01-22 18:08:02
Lemaradt egy előjel: helyesen $-\lim_{n\to \infty} x_n$ .
Előzmény: [154] Lóczi Lajos, 2006-01-22 18:04:48

[154] Lóczi Lajos

2006-01-22 18:04:48

A 2^x=x² egyenlet egyetlen negatív valós gyökét nemelemi függvényekkel fel lehet írni, pl. az ún. Lambert-féle W-függvénnyel, de ezzel a felírással nem mennél túl sokra, mert benne az x $\mapsto$ xe^x függvényt kell invertálni. Az inverz (alkalmas intervallumon) létezik, de "képlettel" (azaz véges sok elemi függvény segítségével) nem írható fel. A transzcendens egyenletek szinte mindig ilyenek, ezen nem kell csodálkozni.

Numerikusan tetszőleges pontossággal megközelíthető a gyök: az első néhány tizedesjegy -0.7666646... A határérték fogalmával szintén könnyedén kifejezhető ez a szám: tekintsük pl. az

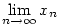x₀=1, $x_{n+1}:=\sqrt{(1/2)^{x_n}}$ rekurziót. Ekkor $\lim_{n\to \infty } x_n$ adja a keresett negatív megoldást.

Előzmény: [146] ScarMan, 2006-01-21 13:15:29

[153] Lóczi Lajos

2006-01-22 17:42:00

Az Általad említett x=(1+1/n)ⁿ, y=(1+1/n)ⁿ⁺¹ (vagy fordítottja) formula (n pozitív egész) a pozitív racionális megoldásokra vonatkozik -- itt egyik feltétel sem teljesül.

(Amúgy azóta a TMCS folyóirat 2003-as számában megjelentek a negatív valós, negatív racionális, illetve komplex megoldásokra vonatkozó eredmények is.)

Előzmény: [147] rizsesz, 2006-01-21 16:10:56

[152] lorantfy

2006-01-22 15:35:30

Di-Lemma: Először azt kellene belátnunk, hogy a sakktábla fekete mezőire helyezett k<32 db ló, mindig k-nál több különböző fehér mezőre üt.

Ha ez igaz, akkor tekintsük a világos mezőkön álló 32 ló elhelyezést.

Tfh. létezik olyan, a feladatnak megfelelő elhelyezés ahol k<32 ló sötét mezőn áll. Akkor ez az elrendezés elérhető úgy, hogy a 32 világos helyről k db lovat sötét mezőre helyezünk. De ezek k-nál több különböző fehér mezőre ütnek, tehát nem ütheti csak a megüresedett k helyet. Ellentmondás.

Márcsak a Di-lemmát kell bizonyítani!

Előzmény: [151] Káli gúla, 2006-01-22 14:34:17

[151] Káli gúla	2006-01-22 14:34:17
Az 1-faktorral látszik, hogy 33-at nem lehet lerakni, de a záródó kör ahhoz kellett, hogy 32-t is csak szabályos elrendezésben lehet.
Előzmény: [150] jonas, 2006-01-22 13:19:17

[150] jonas

2006-01-22 13:19:17

Ez szép megoldás.

Szerintem viszont nem kell tudni, hogy a sakktáblán lehet teljes kört megtenni (ami persze ismert, de ha valaki nem ismeri, akkor nem könnyű belátni). Elég, ha egy 1-faktort megadunk, vagyis párosítjuk a mezőket úgy, hogy minden pár két mezője támadja egymást. Ilyet pedig egyszerű mutatni, például

A	B
C	D
B	A
D	C

és még hét ugyanilyen példány.

Előzmény: [145] ScarMan, 2006-01-21 12:10:33

[149] lorantfy

2006-01-22 10:45:59

Kedves Fórumosok!

Kaptam egy levelet Bodnár Jánostól, aki B. 3869. feladatot javasolta, és azt kéri tőletek, hogy akinek van kedve hozzá, próbálja megoldani a feladatot inverzió segítségével vagy pont körre vonatkozó hatványát felhasználva!

Ha valaki esetleg ilyen megoldást köldött be, jó lenne, ha megosztaná velünk!

[148] lorantfy

2006-01-21 21:24:44

Szia Rizsesz!

Lóczi Lajos cikkében a hatványozás kommutativitásának lehetőségét keresi, az x^y=y^x egyenlet megoldásait.

Alapfeltevés, hogy x,y pozitív valós számok!

Nóra itt most a 2^x=x² egyenlet egy negatív megoldását szeretné megtalálni. Szerintem ezt nem lehet 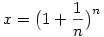$x=\big(1+\frac{1}{n}\big)^n$ alakban felírni.

Előzmény: [147] rizsesz, 2006-01-21 16:10:56

[147] rizsesz	2006-01-21 16:10:56
Lóczi Lajos 2000. januárjában megjelent cikke szerint azt hiszem az a ad b=b ad a egyenlet gyökei a=(1+1/n) ad n és b=(1+1/n) ad (n+1) (TeX :)), illetve az a=b eset. ebből származtatható a 2 megoldás.

[146] ScarMan	2006-01-21 13:15:29
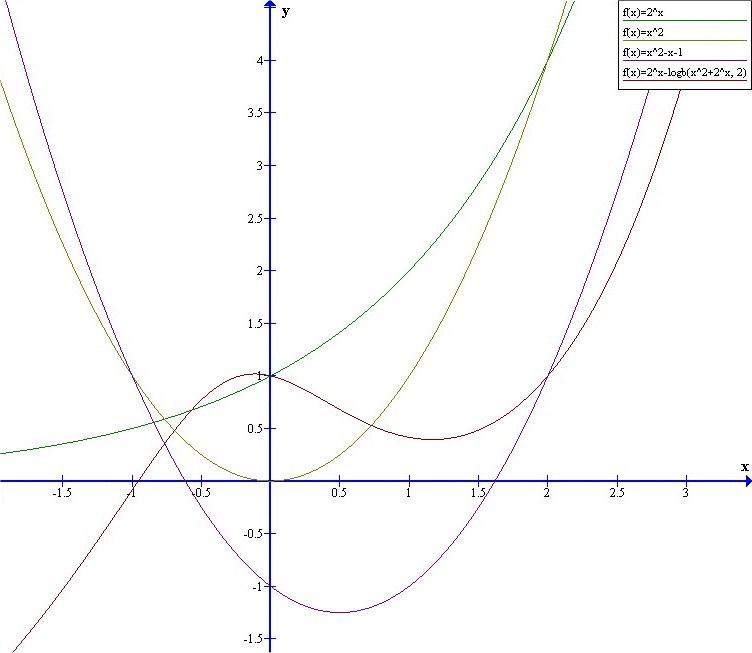
A B.3871. feladathoz: Ha ábrázoljuk koordinátarendszerben az eredeti egyneletet (lila és barna vonal metszéspontjai) és a 2^x=x² egyenletet (zöld és sárga vonal metszéspontjai), látszik, hogy ugyanazok a megoldásiak. Pozitív számok esetén a két gyök 2 és 4, ezek egész számok, így behelyettesítéssel könnyen bizonyítható, hogy ez a kettő a megoldás. De van a negatív számok halmazán is egy megoldás, x₃=-0,76 környékén. Hogy lehetne megoldani a 2^x=x² egyenletet, hogy ezt a gyököt is megkapjuk? Nincs valakinek ötlete?

Előzmény: [139] Iván88, 2006-01-19 19:50:59

Már regisztráltál?
Új vendég vagy?