| [195] jenei.attila | 2006-04-04 23:09:30 |
 A B.3891 feladat megoldása. A feladat: x,y racionális számokra x5+y5=2x2y2. Biz. be, hogy 1-xy egy racionális szám négyzete.
Megoldás: Az egyszerűség kedvéért vezessük be a p=xy jelölést. Az egyenletből:
y5=2p2-x5
. Ezzel a helyettesítéssel írjuk fel p5-t.
p5=x5(2p2-x5)
, vagyis
x10-2p2x5+p5=0
x5-ben másodfokú egyenletet kapjuk. Ebből
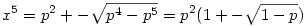
. Mivel x,y racionális 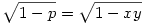 is racionális. is racionális.
|
|
| [194] Mate | 2006-03-24 17:07:19 |
 Igen, azt hiszem, jó ez a megoldás, bár nem számoltam utána. Majd a többivel együtt kijavítom ezt is. Én ilyen megoldást vártam, és Iván hozzászólása alapján nem is értem, hogy lehetett ezt másképpen értelmezni.
|
| Előzmény: [193] [evilcman], 2006-03-24 16:01:00 |
|
|
| [192] Iván88 | 2006-03-24 15:36:01 |
 P.3867. Egyenletes sűrűségű, állandó keresztmetszetű, nyújthatatlan, függőlegesen lógó szál valamilyen L hosszúságnál a saját súlya alatt leszakad. Elképzelhető-e olyan alakú szál, amely akármilyen hosszú lehet, mégsem szakad el a saját súlya alatt?
|
| Előzmény: [191] Mate, 2006-03-24 15:30:48 |
|
| [191] Mate | 2006-03-24 15:30:48 |
 Sziasztok!
A feladatot én tűztem ki, de mivel nekem már nem jár a KöMaL, nem tudom, pontosan hogyan szólt a feladat szövege. Az biztos, hogy én arra gondoltam, amit Onogur írt, hogy a szál keresztmetszetének nagysága változik a hossz függvényében. Hatványfüggvény nem lehet a szál alakja, hiszen ez esetben egy "végtelen" hosszú szál tömege is végtelen nagy. Valaki írja be pontosan a feladat szövegét!
|
|
| [190] Hajba Károly | 2006-03-24 13:52:41 |
 Egy kicsit pontosítanék a felírt képleten, hogy szakszerűbb legyen.
A szakítószilárdsági határ miatt 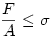
![k\int_x^\infty[f(x)]^2dx \le [f(x)]^2](keplet.cgi?k=8E08B22E2DBCD867)
ahol k egy az anyag sűrűségével és szakítószilárdságával ill. gravitációs gyorsulással arányos és 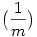 mértékegységű konstans. mértékegységű konstans.
|
| Előzmény: [189] Hajba Károly, 2006-03-24 12:43:54 |
|
| [189] Hajba Károly | 2006-03-24 12:43:54 |
 Üdv!
Szerintem a feladat második mondata nem utal az állandó keresztmetszetre, így valóban forgástestről is lehet szó. Elvileg ebben az esetben nem a (központosan szimetrikus) forma, hanem a keresztmetszeti felület nagysága érdekes, de számolni kör keresztmetszettel célszerű. Gyakorlatilag egy adott magasságban található keresztmetszet nagysága arányos az alatta található végtelen hosszú és egyre vékonyabb "rúd" térfogatával.
A következők csak tipp, mivel kb. 20 éve nem foglalkoztam ezzel. Tehát, ha jó az elképzelésem és jól írom fel a következő egyenletet, akkor ennek megoldása adja a rúd alakjának függvényét.
![\int_x^\infty[f(x)]^2dx = [f(x)]^2](keplet.cgi?k=DAE704663CF4325F)
De gondolom, majd Máté rendberakja a dolgokat. :o)
|
| Előzmény: [187] HoA, 2006-03-24 11:06:09 |
|
| [188] Iván88 | 2006-03-24 12:10:37 |
 Szia HoA!
Én úgy értelmeztem a feladatot, hogyha a keresztmetszete állandó, akkor valamekkora L-nél elszakad.
Szerintem olyan alakúnak kell lennie, hogy a tömege véges legyen, akármilyen hosszú is. Ha a keresztmetszete állandó, akkor nyilván nem beszélhetünk véges tömegről végtelen hosszúság mellett.
Így muszáj neki vékonyodnia.
|
| Előzmény: [187] HoA, 2006-03-24 11:06:09 |
|
| [187] HoA | 2006-03-24 11:06:09 |
 Lehet, hogy nem jól értem a feltételeket, de nekem az "Egyenletes sűrűségű, állandó keresztmetszetű, nyújthatatlan, függőlegesen lógó szál" azt jelenti, hogy egy hengerszerű testről van szó, melynek tömege és így súlya is egyenesen arányos az L hosszúsággal. Ez áll az állandó keresztmetszet miatt az egységnyi keresztmetszetre ható erőre is. Ha feltételezzük, hogy a szál szakítószilárdsága véges 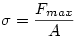 , kellően hosszú szál esetén biztosan elszakad. Csak az nem világos, hogy merül fel egyáltalán a keresztmetszet alakja. , kellően hosszú szál esetén biztosan elszakad. Csak az nem világos, hogy merül fel egyáltalán a keresztmetszet alakja.
|
| Előzmény: [186] Iván88, 2006-03-23 21:38:29 |
|
| [186] Iván88 | 2006-03-23 21:38:29 |
 Sziasztok!
A P.3867.-esre van valakinek megoldása?
Az én tippem az, hogy a szál alakja legfeljebb valamilyen 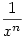 tengelymetszetű forgástest lehet, de ez sak tipp. tengelymetszetű forgástest lehet, de ez sak tipp.
|
|
|
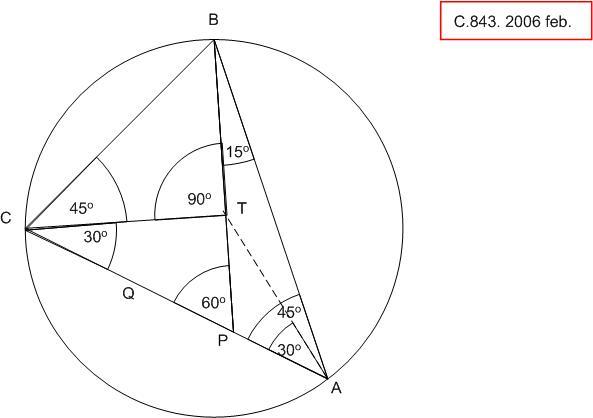
| [184] HoA | 2006-03-20 10:44:57 |
 C.842 helyett C.843
A megoldás természetesen jó, de kicsit "deus ex machina". Ugyanezeket az elemeket felhasználva egy konstruktív megoldás:
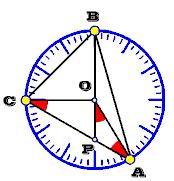
BPC  = 45 + 15 = 60o . Bocsássunk merőlegest C-ből BP-re, talppontja legyen T. Ekkor CPT 60o -os derékszögű = 45 + 15 = 60o . Bocsássunk merőlegest C-ből BP-re, talppontja legyen T. Ekkor CPT 60o -os derékszögű  , PT = PQ = PA . PAT egyenlőszárú , PT = PQ = PA . PAT egyenlőszárú  , TAP , TAP  = 30o , BAT = 30o , BAT  = 15o . TCA egyenlőszárú = 15o . TCA egyenlőszárú  ( két 30o -os szög ) TC = TA, TAB egyenlőszárú ( két 30o -os szög ) TC = TA, TAB egyenlőszárú  ( két 15o -os szög ) TB = TA . Így TC = TB, TBC derékszögű ( két 15o -os szög ) TB = TA . Így TC = TB, TBC derékszögű  egyenlőszárú, TCB egyenlőszárú, TCB  = 45o . (És persze kiderül, hogy T tkp. O ) = 45o . (És persze kiderül, hogy T tkp. O )
|
 |
| Előzmény: [179] Káli gúla, 2006-03-19 14:52:01 |
|
| [183] lorantfy | 2006-03-20 10:24:36 |
 Ötletes megoldás! Kérdés: rögtön így ugrott be, vagy megoldottad másként és utánna raktad be a körbe? Én is gondolkodtam szögfüggvénymenetes megoldáson, találtam is de elég körülményes lett.
|
| Előzmény: [179] Káli gúla, 2006-03-19 14:52:01 |
|
|
| [181] jonas | 2006-03-19 21:04:16 |
 A,1,2,3,4,5,6,7,8,9,10,J,D,K helyett inkább csak A,2,3,4,5,6,7,8,9,10,J,D,K.
|
| Előzmény: [180] lorantfy, 2006-03-19 19:04:19 |
|
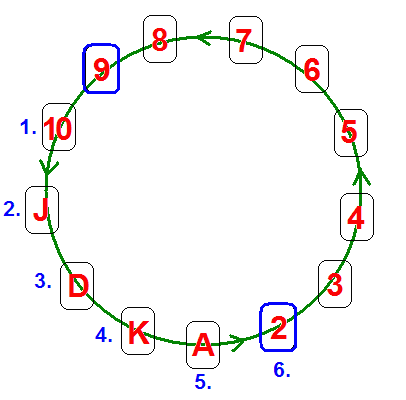
| [180] lorantfy | 2006-03-19 19:04:19 |
 B. 3889. megoldása: Az 52 lapos francia kártyában négy "szín" van: káró, kör, pik és treff. Minden színből 13 lap. Jelöljük ezeket A,1,2,3,4,5,6,7,8,9,10,J,D,K jelekkel.
Az 5 lap között, amit a néző kiválasztott biztosan van két azonos színű lap. (Ha kettőnél több azonos színű van akkor a segéd kiválasztja a két sorban legközelebb állót.) A bűvész és segédje előre megegyeznek, hogy ezek közül egyik lesz majd az 5. lap, amit a bűvésznek ki kell találnia.
Helyezzük el a 13 azonos színű lapot egy kör kerületén egy adott (előre megbeszélt) sorrendben. Jelöljük ki a körben a kiválasztott két lapot. (Pl. 9-es és 2-es az ábrán) 13-2=11. Így a két lap között egyik irányban max. 5 lap van. Haladjunk pozitív a körüljárás irányában. Ezen 5 lap előtt álló kiválasztott kártya (ábrán a 9-es) legyen a kezdő, a másik pedig (ábrán a 2-es) a záró kártya.
A segén először a kezdő kártyát fogja átadni a bűvésznek. Ebből a bűvész tudja, hogy milyen színü az utolsó (kitalálandó kártya) és azt is tudja, hogy a körben pozitív körüljárás szerint a kezdő kártyát követő 6 kártya között van.
Hogy pontosan hányadik lapról van szó, azt pedig már a maradék három kártya sorrendjével lehet kódolni, hiszen 3 kártya 6 féleképpen rakható sorba.
Pl. a következőképpen: Előre megállapítanak a színek között egy nagyságrendi sorrendet. Pl. káró<kör<pik<treff. A figurák között pedig pl. A<1<2...J<D<K. Így a 3 lap nagyságrendbe rakható. Jelöljük őket 1,2,3 számjegyekkel. A permutációkat háromjegyű számként nagyságszerint sorbarakva:
123=1, 132=2, 213=3, 231=4, 312=5, 321=6.
A bűvész a 3 db egymásután átadott lapból visszakódolja a sorszámot és az első átadott kártyából ennyit előre lépve a körben meg tudja nevezni az utolsó lapot.
|
 |
|
|
|
| [177] Iván88 | 2006-03-09 20:45:10 |
 A P. 3862.-re van valakinek megoldása?
|
|
| [176] Yegreg | 2006-02-27 20:29:44 |
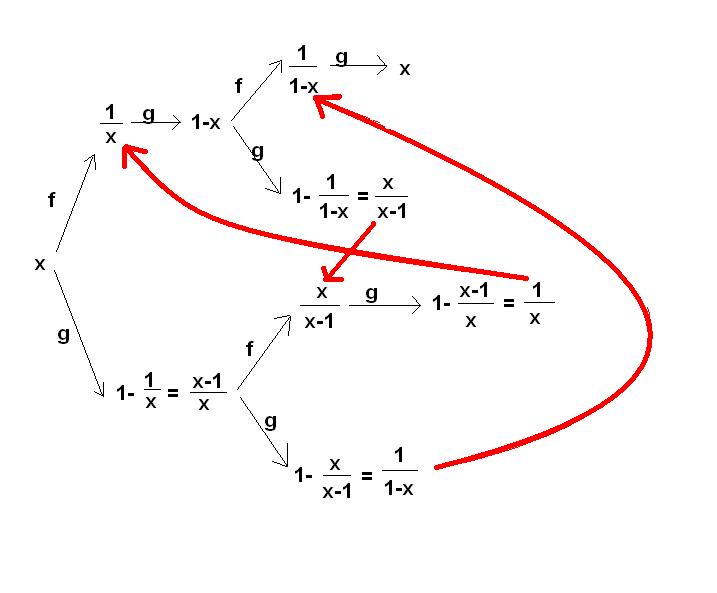
 B.3851, szerintem meglehetősen egyszerű megoldás:) Itt fk(x) alatt fofo...of(x)=f(f(...f(x))..)-et értettem.
Először is, nézzük meg az f2 és a g3 függvényeket! 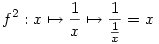 , azaz , azaz
. 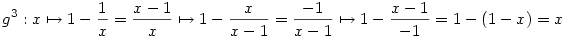 , azaz , azaz
. Ha előállítható az x x+1 függvény, akkor az azt jelenti, hogy véges sok lépésben el kell jutnunk a függvények felhasználásával x-ből x+1-be, azonban (1) és (2) alapján az egymás után kétszer végrehajtott f, illetve háromszor végrehajtott g függvények kiesnek. Ebből következően a valóban előre vivő lépések: x+1 függvény, akkor az azt jelenti, hogy véges sok lépésben el kell jutnunk a függvények felhasználásával x-ből x+1-be, azonban (1) és (2) alapján az egymás után kétszer végrehajtott f, illetve háromszor végrehajtott g függvények kiesnek. Ebből következően a valóban előre vivő lépések:
1, ha utoljára f függvényt hajtottunk végre, akkor most értelmetlen újra f-et végrehajtani, mert akkor a kettővel ezelőtti pozícióba jutnánk, így f után csak g-t hajtunk végre.
2, ha utoljára g-t hajtottunk végre, és az előtt is, akkor, ha most is g-t hajtanánk végre, akkor a hárommal ezelőtti pozícióba jutnánk, ami értelmetlen, azaz 2 g függvény után csak f következhet.
3, ha utoljára g-t hajtottunk végre, de előtte nem g-t, akkor mind az f, mind a g függvény végrehajtható.
Ezek alapján nézzük meg, hova juthatunk x-ből!
A vékonyabb fekete vonalak a függvényeket, a vastagabb piros vonalak egyenlőségeket jelölnek. Látható az ábráról, hogy a fent leírt lépésekkel véges sok lépésen belül egy korábbi pozícióval, vagy x-szel egyenlő értéket kapunk, és ezek között nem szerepel az x+1, ebből nyilvánvalóan következik, hogy nem állítható elő a függvények kompozíciójaként, hiszen csak az ábrán látható "kör" elemei állhatnak elő.
|
 |
|
| [175] Yegreg | 2006-02-27 20:24:47 |
 B.3867.
Nyilvánvalóan, ha n nem háromhatvány, akkor felírható 3k(3l+1) vagy 3k(3l+2) alakban, hiszen 3kA alakban triviálisan felírható(pl. k=0 egyértelműen jó), és innentől, ha 3|A, akkor kiemeljük, és  alakba írjuk, ha a harmada osztható 3-mal, akkor ismét kiemeljük, a kitevőt 1-gyel növeljük, és ez mindaddig folytathatjuk, míg a kapott A' szám nem lesz osztható 3-mal, ekkor pedig a kívánt alaknál járunk. alakba írjuk, ha a harmada osztható 3-mal, akkor ismét kiemeljük, a kitevőt 1-gyel növeljük, és ez mindaddig folytathatjuk, míg a kapott A' szám nem lesz osztható 3-mal, ekkor pedig a kívánt alaknál járunk.
1. állítás
23k+1 1(43k+23k+1) 1(43k+23k+1) | (1) |
Bizonyítás:
Az állítás ekvivalens azzal, hogy
(43k+23k+1)|(23k+1-1), a kongruencia definíciója alapján.
23k+1-1=(23k-1)3-1=(23k-1)((23k)2+23k+1)=(23k-1)(43k+23k+1)
Tehát, mivel 23k-1 nyilván egész, így (1) teljesül.
2. állítás
23k(23k+1) -1(43k+23k+1) -1(43k+23k+1) | (2) |
Bizonyítás:
Az állítás ekvivalens azzal, hogy
(43k+23k+1)|(23k(23k+1)+1).
23k(23k+1)+1=(23k)2+23k+1=43k+23k+1
Tehát a kifejezés egyenő vele, azaz nyilván osztható is.
3. állítás
23k2(23k2+1) -1(43k+23k+1) -1(43k+23k+1) | (3) |
Ez ekvivalens azzal, hogy
(43k+23k+1)|(23k2(23k2+1)+1)
23k2(23k2+1)+1=43k2+23k2+1=43k2-43k.23k+43k+43k.23k-43k+23k+43k-23k+1(hozzáadtuk és kivontuk ugyanazokat a számokat)=43k(43k-23k+1)+23k(43k-23k+1)+43k-23k+1=(43k+23k+1)(43k-23k+1)
És mivel 43k-23k+1 nyilván egész, így az állítás teljesül.
(a későbbiekben használt k független ezen k-któl, ezek tetszőleges természetes k-ra igaz állítások)
1, eset
n=3k(3l+1)
4n+2n+1=2n(2n+1)+1=23k(3l+1)(23k(3l+1)+1)+1=(23k+1)l.23k((23k+1)l.23k+1)+1 ((1) alapján) (1)l.23k((1)l.23k+1)+1=23k(23k+1)+1((2) alapján) (1)l.23k((1)l.23k+1)+1=23k(23k+1)+1((2) alapján) -1+1=0(43k+23k+1) Azaz osztható a kifejezés 43k+23k+1, viszont, ha n -1+1=0(43k+23k+1) Azaz osztható a kifejezés 43k+23k+1, viszont, ha n 3k, azaz l 3k, azaz l 0, tehát n nem háromhatvány, akkor a kifejezés nem egyenlő 43k+23k+1-vel, így van önmagán kívüli és 1-től különböző pozitív osztója, tehát nem prím. 0, tehát n nem háromhatvány, akkor a kifejezés nem egyenlő 43k+23k+1-vel, így van önmagán kívüli és 1-től különböző pozitív osztója, tehát nem prím.
2, eset
n=3k(3l+2)
4n+2n+1=2n(2n+1)+1=23k(3l+2)(23k(3l+2)+1)+1=(23k+1)l.23k2((23k+1)l.23k2+1)+1((1) alapján) 23k2(23k2+1)+1((3) alapján) 23k2(23k2+1)+1((3) alapján) -1+1=0(43k+23k+1) -1+1=0(43k+23k+1)
Tehát a kifejezés osztható 43k+23k+1-vel, és mivel 3l+2 biztosan nagyobb 1-nél, hiszen l természetes szám, így a kifejezés nem egyenlő 43k+23k+1-gyel, tehát van 1-től és önmagától különböző pozitív osztója, így nem prím.
Ezzel az állítást bebizonyítottuk, hiszen beláttuk, hogy minden olyan esetben, amikor n nem 3k alakú, a kifejezés összetett.
|
|
| [174] Yegreg | 2006-02-27 20:23:25 |
 Ha már én kérvényeztem, hogy elérhető legyen a TeX forrás, illik pár megldást feltöltenem.
|
|
| [173] Sabroso | 2006-02-27 19:01:22 |
 A 'hivatalos' megoldás viszont ehhez képest nem túl szép... Ami érdekes, mert a 159 megoldó közül valószínűleg egy páran rájöttek erre a megoldásra (pl. én is).
|
| Előzmény: [170] HoA, 2006-02-27 17:26:51 |
|
|
|







 =ACD
=ACD mert a DA iven nyugvó kerületi szögek. ABD
mert a DA iven nyugvó kerületi szögek. ABD egyenlő szárú és egyenlő szárú a DMF
egyenlő szárú és egyenlő szárú a DMF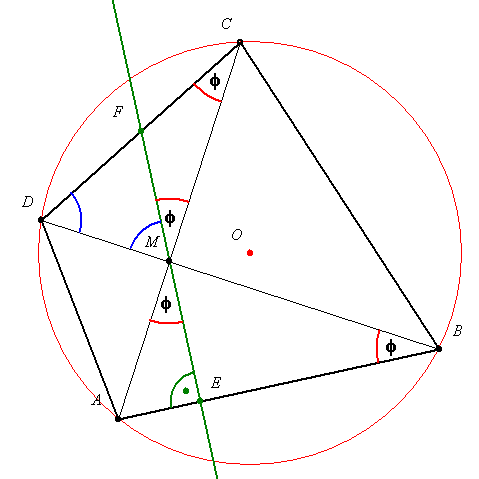





 x+1 függvény, akkor az azt jelenti, hogy véges sok lépésben el kell jutnunk a függvények felhasználásával x-ből x+1-be, azonban (1) és (2) alapján az egymás után kétszer végrehajtott f, illetve háromszor végrehajtott g függvények kiesnek. Ebből következően a valóban előre vivő lépések:
x+1 függvény, akkor az azt jelenti, hogy véges sok lépésben el kell jutnunk a függvények felhasználásával x-ből x+1-be, azonban (1) és (2) alapján az egymás után kétszer végrehajtott f, illetve háromszor végrehajtott g függvények kiesnek. Ebből következően a valóban előre vivő lépések: 
 1(43k+23k+1)
1(43k+23k+1) 3k, azaz l
3k, azaz l