|
| [219] ScarMan | 2006-05-08 21:16:44 |
 Én is csináltam a feladatra egy animációt Euler 3D-ben, letölthető innen.
|
|
| [218] Hajba Károly | 2006-05-08 15:09:07 |
 Ivánnak az utolsó 6. fázis moziját küldtem el és ebből egy kép, melyet László betett.
Aki igényli és küld egy drótpostát nekem, annak visszaküldöm mind a 6 fázis moziját. Reményeim szerint a megoldás mellékleteként a honlapra is felkerül, ha eljön az ideje.
|
|
|
| [216] lorantfy | 2006-05-08 12:31:08 |
 Kedves Iván!
Külföldön voltam 10 napig, így csak most tudok válaszolni.
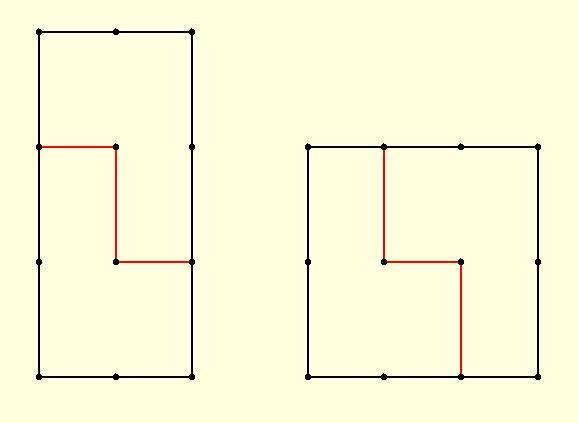
A lenti síkbeli módszer a téglalap egyik oldalát 2/3-ára csökkenti, a másik oldalt 3/2 szeresére növeli.
Van egy 8x8x27 oldalú téglatestünk. Először elvágjuk az egyik 8x27-es téglalap felől. Összeillesztjük a darabokat és 12x8x18 méretű téglatestet kaponk.
Majd elvágjuk ezt a téglatestet a 8x18-as oldal felöl és összeillesztve a darabokat 12x12x12-es kockát kapunk.
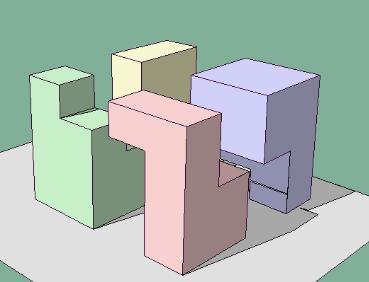
Hajba Károly barátom nagyon szép mozgóképes ábrákat készített a darabolásról. Ebből egyenlőre egy kivágott képet teszek fel.
|
 |
| Előzmény: [214] Iván88, 2006-04-28 21:01:28 |
|
| [215] ScarMan | 2006-04-30 14:06:22 |
 Én is ebből indultam ki, innen továbbvittem koordináta-geometriával és ki is jött a hiperbola, az volt a vicces, hogy mind a két ágát megkaptam, pedig a feltételek alapján csak az egyik lett volna jó (csak a 30°osnál jön ki a lefelé álló szabályos háromszög). Gondolom valami négyzetreemelésnél vagy ilyesminél bejött mégegy előjel, nem tudom... Nem találtam meg, hogy hol, beküldtem úgy ahogy volt, és odaírtam a végére, hogy 'mellesleg csak az egyik ága jó...' :) Ha 4 pontot kapnék rá, már az is jó lenne. A darabolósat én se csináltam meg, a másik két 5pontosom remélem jó. Én nem csináltam meg a magasság-felezőmerőlegeseset sem. Az x5+y5 nekem meglepően hamar kijött, szerencsém volt.
|
| Előzmény: [206] Iván88, 2006-04-20 21:42:58 |
|
|
|
| [212] lorantfy | 2006-04-21 21:43:18 |
 Kedves KöMaL Megoldók!
Azoknak, akik nem boldogultak a B. 3895. (darabolós) feladattal, egy kis síkbeli segédpéldát szeretnék adni, amit megoldva aztán rögtön rá lehet jönni az eredeti feladat megoldására.
Vágjunk szét egy 9x4 egység méretű téglalapot két olyan részre, amiből négyzetet lehet összerakni!
A méretekből lehet következtetni, ha nem megy akkor a nevem kezdőbetűje a segítség!
|
| Előzmény: [210] [evilcman], 2006-04-21 11:46:53 |
|
|
|
| [209] Sabroso | 2006-04-21 11:00:31 |
 Nekem is ugyanez a hiperbola jött ki. Az én megoldásom ennél annyival bonyolultabb, hogy az abszolútérték-jeleid helyén én külön-külön megvizsgáltam a lehetséges előjeleket (de ez csak azért volt, mert először csak a +30 fokos esetet kerestem). Egyébként érdekes, hogy ha a hiperbolának lenne metszéspontja a vezéregyenessel, akkor az a két pont nem lenne jó (ott ugyanis a bezárt szög tangense nem lenne értelmezve, a meredekségek szorzata -1 lenne). De hát nem lesz...
Mindenesetre szerintem ebben a tanévben ez volt a legnehezebb feladatsor eddig. Négy ötpontos példa volt és egyik se túl egyszerű. Nekem például sokkal jobban tetszett az az x5+y5-es. Rengeteget kellett rajta gondolkozni, de aztán nem tartott olyan sokáig leírni. A 3901. leírása nekem két és fél oldal lett. Hasonlóképp a 3900.-é is, a másik kettőt meg meg se bírtam oldani :-)
|
| Előzmény: [208] [evilcman], 2006-04-20 22:38:21 |
|
|
| [207] Sabroso | 2006-04-20 21:46:43 |
 Bocsi, de azt a 'szakadásmentes'-t kifejtenéd? Nekem ugyanis hiperbola jött ki koordinátageometriával.
Persze érdekes kérdés, hogy a 30o-os szöget bezáró érintők az érintőszakaszokat vagy az egyeneseket jelentik. Ha az előbbi, akkor csak a hiperbola alsó ága lesz megfelelő, szerintem ezt találhattad meg.
|
| Előzmény: [206] Iván88, 2006-04-20 21:42:58 |
|
| [206] Iván88 | 2006-04-20 21:42:58 |
 Sziasztok. Elakadtam a B.3901-essel (Az a parabolás)
Odáig jutottam, (sajnos ábrát nem tudok feltölteni) hogy (A parabola fókusza F, vezéregyenese v,) Az összes ilyen P pontra igaz, hogy a P középpontú PF sugarú körök metszéspontjait v-vel E1-gyel és E2-vel jelölve a PE1E2 háromszög szabályos. (Kiss György tavalyi kúpszeletes cikkében van néhány hasznos infó, de nem elég...)
A keresett alakzat nyilvánvalóan szimmetrikus az F-ből v-re bocsájtott merőleges egyenesre, biztosan szakadásmentes és nyítl.
Euklidesszel megnéztem, és 99,9999 százalék, hogy a keresett alakzat szintén parabola, de itt akadtam el.
Valaki aki tud segítsen. (Koordináta-renszerbe betéve semeddig sem tudtam eljutni, szerintem túl sok jó megoldás nem lesz :o) )
|
|
| [205] rizsesz | 2006-04-20 15:52:35 |
 mármint az én időmben, azaz 2002-ben :)
|
|
| [204] rizsesz | 2006-04-20 15:52:15 |
 emellett még a 11. osztályos matek oktv 2. és döntő fordulójából is volt példa...
|
|
| [203] Sümegi Károly | 2006-04-20 15:50:37 |
 Idén eddig legalább 10-15 olyan feladat volt B-ben, ami könyvekben megtalálható. Ezt nem tartom kifejezetten szerencsésnek. Ezt a feladatot én nem találtam meg, de ki tudja mennyi feladatot tűztek ki még máshol.
|
| Előzmény: [202] rizsesz, 2006-04-20 00:57:37 |
|
| [202] rizsesz | 2006-04-20 00:57:37 |
 A B.3875.-höz kapcsolódóan a 2002. májusi szám egyik feladata:
B.3555. Egy 2n+1-tagú társaság bármely n-tagú csoportjához van a társaságnak olyan a csoporthoz nem tartozó tagja, aki a csoport minden tagját ismeri. Az ismeretséget kölcsönösnek tételezzük fel. Bizonyítsuk be, hogy a társaságnak van olyan tagja, aki mindenkit ismer. (5 pont) ...
|
|
| [201] Iván88 | 2006-04-06 15:13:30 |
 Kösz!
Az igazat megvallva nekem volt hozzá könyvem, onnan néztem ki, de ez nem tilos.
De azért ez az 5 pontosok között is egy nehezebb feladat volt.
Én hamar eljutottam odáig, hogy
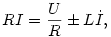
innentől a diff. egy. az kézenfekvő, csak nem tananyag...
|
| Előzmény: [200] CsG, 2006-04-05 22:58:59 |
|
| [200] CsG | 2006-04-05 22:58:59 |
 Igen, diff. egyenlet nélkül is megoldható. Ha felhasználod, hogy a fluxus egyenesen arányos az áramerősséggel, és hogy a fluxus hirtelen nem változhat (tehát állandó). Ellentétes tekercselésnél a fluxusok kivonódnak egymásból, azonos menetiránynál pedig összeadódnak. Ezekből is ugyanúgy kijön, amire te is jutottál.
|
| Előzmény: [199] Iván88, 2006-04-05 20:19:34 |
|
| [199] Iván88 | 2006-04-05 20:19:34 |
 Már régen írtam megoldást!
A P.3872.-esre a megoldásom: (sajnos az ábrát nem bírta a rendszer feltölteni)
A kapcsolós ág a Kettes, a másik az 1-es. A Kettes ág nyitva van, tehát ott nyitás után semmikor sem folyhat áram. (feszültség persze indukálódik...)
Az 1-esben viszont:
a) Ha a tekercselés azonos, akkor a vasmagman-nyitás előtt-a mágneses indukció nagysága(jó közelítéssel) 0 .
Ha nyitjuk a Kapcsolót, akkor bekapcsolási jelenséget figyelhetünk meg. Azaz az indukált feszültség és a telep feszültsége egymást rontja. Mint ismeretes:
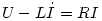
Ez I-re egy elsőfokú differenciálegyenlet, azaz
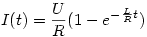
(Mivel I(0)= ) Tehát ) Tehát  . Így közvetlenül a nyitás után sehol sem folyik áram. . Így közvetlenül a nyitás után sehol sem folyik áram.
b) Itt viszont nyitás előtt a B-k egymást erősítik, azaz az egyes tekercsek mégneses indukciója (mely mindkét tekercsnél ugyanakkora) fele a vasmagban lévőnek. Nyitás után a B értéke a felére csökken, tehát egy kikapcsolási jelenség figyelhető meg nyitáskor, így az indukált feszültség( ), és a telep feszültsége egymást erősítik. Így: ), és a telep feszültsége egymást erősítik. Így:
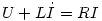
. Ennek a megoldása:
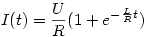
(I(0)=UR) Tehát

Tehát ez esetben az áramerősség értéke kezdetben a nyitás előttinek a duplája.
De vajon differenciál egyenletek nélkül ez megoldható?
|
|
|
|
| [196] Sabroso | 2006-04-05 17:05:03 |
 Bocs, de ezt nem értem. Ha x és y racionálisak, abból szerintem nem következik, hogy 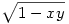 is racionális. is racionális.
Viszont az én megoldásom szerintem jó, csak eléggé kitalálhatatlan: Osszunk át x2y2-tel (x=y=0-ra nyilván igaz az állítás)
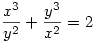
Jelöljük most  -et a-val! Ekkor -et a-val! Ekkor
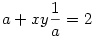
Ahonnan a-val fölszorozva
a2-2a=-xy
, tehát
(a-1)2=a2-2a+1=1-xy
Persze az egy jó kérdés, hogy miért nem szimmetrikus az a... Megpróbáltam végig levezetni, de egy kicsit hosszadalmas, úgyhogy inkább nem írnám le :)
|
| Előzmény: [195] jenei.attila, 2006-04-04 23:09:30 |
|