| [363] Maga Péter | 2007-12-24 21:25:21 |
 Elnézést, hogy csak így beleszólok - kérdezek... a B.4020 jelű feladatnál a "poliéder" nem volt egy kicsit szerencsétlen szóhasználat, ebbe egyesek beleértik a konvexitást?
|
|
| [362] Róbert Gida | 2007-12-18 14:46:16 |
 Kömal A.437 megoldása, (jó rövid lesz): D. O. Skljarszkij-N. N. Csencov-I. M. Jaglom Válogatott feladatok és tételek az elemi matematika köréből című könyv 60.a feladat szerint, ha p>3 prím, akkor 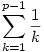 összeg olyan tovább nem egyszerűsíthető tört, amelynek a számlálója osztható p2-tel. Bizonyítás a könyv végén. Ez egyébként Wolstenholme tétele. összeg olyan tovább nem egyszerűsíthető tört, amelynek a számlálója osztható p2-tel. Bizonyítás a könyv végén. Ez egyébként Wolstenholme tétele.
Nekünk azonban még az  tag is benne van a feladatban, hát adjuk hozzá, kapjuk: tag is benne van a feladatban, hát adjuk hozzá, kapjuk:
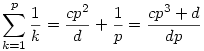
, ahol persze használtam az előző feladatot és itt lnko(c,d)=1 tovább nem egyszerűsíthető felírásban. De 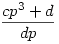 sem egyszerűsíthető tovább, azaz lnko(cp3+d,dp)=1 teljesül, hiszen lnko(cp3+d,d)=lnko(cp3,d)=lnko(c,d)=1, hiszen p és d relatív prímek, mert triviálisan d osztója (p-1)!-nak, de p prím, így relatív prím (p-1)!-hoz. Továbbá lnko(cp3+d,p)=lnko(d,p)=1 az előzőek miatt szintén. Így d-hez és p-hez is relatív prímcp3+d, de akkor pd-hez is. Azaz a feladat jelöléseit használva valamely T egészre a felírás a következő alakú a=T(cp3+d) és b=T(dp) lesz, hiszen a redukált alak sem egyszerűsíthető tovább, azaz lnko(cp3+d,dp)=1 teljesül, hiszen lnko(cp3+d,d)=lnko(cp3,d)=lnko(c,d)=1, hiszen p és d relatív prímek, mert triviálisan d osztója (p-1)!-nak, de p prím, így relatív prím (p-1)!-hoz. Továbbá lnko(cp3+d,p)=lnko(d,p)=1 az előzőek miatt szintén. Így d-hez és p-hez is relatív prímcp3+d, de akkor pd-hez is. Azaz a feladat jelöléseit használva valamely T egészre a felírás a következő alakú a=T(cp3+d) és b=T(dp) lesz, hiszen a redukált alak 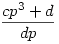 . Így . Így
ap-b=T(cp4+dp-dp)=Tcp4
ami valóban osztható p4-nel. Készen vagyunk.
|
|
| [361] Róbert Gida | 2007-11-17 13:43:39 |
 Kömal A. 436. megoldása: Indirekt tegyük fel, hogy n pozítiv egész és
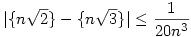
Legyen
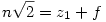 | (1) |
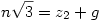 | (2) |
Ahol z1 és z2 a számok egészrészei, míg f és g a számok törtrészei. Így a feladat szerint
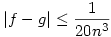 | (3) |
Vonjuk ki a (2)-es egynletből az (1)-est, kapjuk:
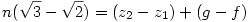
Osszuk el n-el és legyen z2-z1=p egész szám, ekkor:
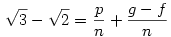
Kivonva az egyenletből 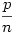 -et és (3)-at használva kapjuk: -et és (3)-at használva kapjuk:
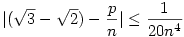 | (4) |
A háromszög-egyenlőtlenséget és (4)-et használva:
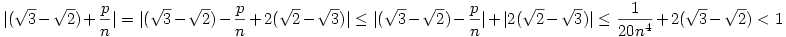
Azaz:
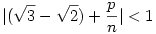 | (5) |
(4)-et és (5)-öt összeszorozva, kapjuk:
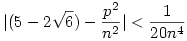 | (6) |
Újra a háromszög-egyenlőtlenséget és (6)-ot használva:
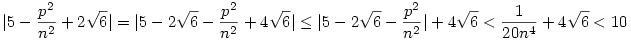
Azaz
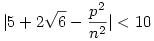 | (7) |
(6)-ot és (7)-et összeszorozva:
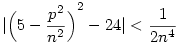 | (8) |
Az egyenlőtlenséget n4-gyel szorozva kapjuk:
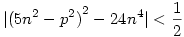
De a bal oldalt nemnegatív egész szám áll, így csak nulla lehet, azaz
(5n2-p2)2-24n4=0
Azaz
(5n2-p2)2=24n4
, ami nem lehet, mert bal oldalon négyzetszám áll, míg a jobb oldalon nem, amint az könnyen látható. Így ellentmondást kaptunk, így igaz a feladat állítása.
|
|
|
| [359] sakkmath | 2007-11-06 09:19:54 |
 Az A433., szeptemberi feladat megoldása a komal.hu-n egy elírással jelent meg .
Az (1a) sor első '=' jele téves, a helyére '+' jelet kell írni.
|
|
| [358] rizsesz | 2007-10-31 13:04:26 |
 Nem ismerem :) de a neve alapján nem merek nyilatkozni ilyesmikről. Tavaly a C-ben volt egy hatodikos amerikai lány, aki csak angolul küldött megoldásokat.
|
| Előzmény: [357] jonas, 2007-10-31 12:00:23 |
|
|
|
|
| [354] rizsesz | 2007-10-30 15:20:26 |
 Én pont most láttam egy Amerikából versenyző fiatalt az A-ban. :)
|
|
|
| [352] vogel | 2007-10-21 13:40:20 |
 A B.4013. is rosszul volt fordítva. Ki lehet-e színezni a pozitív racionális számokat... Angolul: s it possible to colour the positive integers... Ami ugye egész számokat ír.
|
|
| [351] Python | 2007-10-21 13:17:30 |
 Szerintem a mostani K.136. feladat félre van fordítva az újságban:
Magyar:
"Az iskola fiútanulóinak 70%-át az első, lánytanulóinak 80%-át a második csoportba osztották be."
Angol:
"70% of the boys and 80% of the girls were in the first group."
Mellesleg az angolt nem lehet megoldani...
|
|
| [350] Kisfox | 2007-08-16 09:31:06 |
 az en nevem varga bonbien es en raktam fel az artofproblemsolvingra a feladatokat. Az A matekokat azert mert tortem rajtuk a fejemet, de nem jutottam megoldasra, igy kivancsi lettem a megoldasukra, es kertem a velemenyet a forumozoknak. Aztan ha mar kaptam tippeket gondoltam (nagyon rosszul) hogy miert ne adjak be roluk megoldast. hasonlo volt a helyzet egy par B vel. a fizikakat amiket felraktam viszont csak azutan tettem hogy megoldottam oket. a p3992 feladattal kapcsolatban meg azt tudom mondani, hogy semmifele kiszivargasrol nincsen szo. nezzetek csak meg a komal 2006 januarjaban kituzott p3860 as feladatot. lathato hogy mar akkor meg kaptam ra az 5 pontot, es az is lathato hogy ezt a feladatot tuztem ki a forumon. az meg pusztan veletlen hogy pont a majusi rakovetkezo ujsagban volt egy hasonlo feladat.
ezennel kifejezm mely sajnalatomat eme nagyon rossz tettemert, es sajnalom hogy ha a szerkesztosegnek fejfajast okoztam. Nagyon elveztem oldani a komal feladatait, es pusztan tulzott erdeklodesem okozta a vesztem.
Varga Bonbien
|
|
| [349] lorantfy | 2007-08-09 11:15:49 |
 Mindegy, hogy hány lakosú a falu, ha több mint 103. Ugyanis előfordulhat, hogy a lakosok közül 103 fő alakít 104 (vagy annál több) klubot és a többi lakos nem vesz részt a klubalakításban.

Ez azt jelenti, hogy 103 fő akár 5253 legalább 1 tagban különböző klubot is alakíthat. Törvényes képviselője viszon csak 103-nak lehet, mert csak ennyi emberünk van.
A jogi bizottság ezért nem engedélyezheti, hogy 103-nál több klub jöjjön létre. Hiszen, ha engedélyezné 104 klub létrehozását, akkor 103 lakos összeállhatna és alakíthatna mondjuk 104 klubot és a 104. klubnál már nem lehetne törvényes képviselőt találni.
Láttuk, hogy 101 és 102 klub létrehozása engedélyezhető.
Egyetlen kérdés maradt, - és ez a feladat legszebb része - hogy 103 db klub esetén lehet-e mindig törvényes képviselőt választani.
A válasz: igen, már csak meg kell mondani hogyan!
|
| Előzmény: [348] öreg, 2007-08-09 09:41:28 |
|
| [348] öreg | 2007-08-09 09:41:28 |
 A B.4011.-nél a magyarázat érthető. De hiányzik a megoldás összefoglalása a végén: Mivel egy n>101 lakosú faluban éppen n darab ilyen egyesület hozható létre, tehát a 2007 lakos 2007 egyesületet alapíthat.(???) A polgármester végülis nem matematikus, nem az elméletre kiváncsi, hanem arra, hogy hány egyesület alakulhat...
|
| Előzmény: [347] lorantfy, 2007-08-08 13:42:12 |
|
| [347] lorantfy | 2007-08-08 13:42:12 |
 Kedves Öreg!
Szeretnék Neked segíteni a B.4011. feladat megoldásának megértésében és másnak is akit érdekel.
Idemásolom a feladatot, hogy ne kelljen keresgélni:
B. 4011. A 2007 lakosú Egyesületfalva lakói nagyon szeretnek klubokat alakítani. A település polgármestere a következő szabályokat hozza:
(1) minden klubnak pontosan 101 taggal kell rendelkeznie, és
(2) két különböző klubnak nem lehet azonos a tagsága. A város szenátusában mindegyik klubot az egyik tagja képviseli, és a törvény szerint semelyik két klubnak nem lehet ugyanaz a személy a képviselője. A jogi bizottság úgy szeretné korlátozni a klubok számát, hogy azok bárhogyan is alakuljanak a szabályok betartásával, mindig lehessen törvényesen képviselőket találni. Legfeljebb hány klub megalakítását engedélyezheti a bizottság?
A falu lakóinak száma nem igazán lényeges, csak annyira, hogy nagyobb mint 104. Ugyanis az összes esetek közül azok az érdekesek, ahol kevés emberből alakulnak a 101 tagú klubok, hiszen akkor lehet, hogy nem lesz elég képviselő.
Ha csak 101 klub alakul akkor minden klubban biztosan tudunk képviselőt választani, mert a tagok között legfeljebb 100 másik klub képviselője lehet és a maradék egy ember lehet a képviselő.
Ha 102 egyesület alakul, akkor ahhoz legalább 102 emberre van szükség. Tehát megvan a 102 képviselőnk. De előfordulhat, hogy a 102. klub képviselőválasztásán kiderül, hogy éppen a többi 101 klub képviselői vannak jelen. Ekkor kiválasztunk egy x jelenlévő tagot, aki a X klubban képviselő. X klubnak van 102. klubtól különböző tagja y, aki nem képviselő. Mostantól y lesz az X klub képviselője, x pedig a 102. klubbé.
Ha 104 klubot engedélyezne a bizottság, akkor már gond lehet a képviselő választással. Ugyanis 104 klubot már 103 emberből is létre lehet hozni a szabályok szerint, de akkor 1 klubnak biztos nem lesz képviselője.
Engedélyezhetnek-e 103 klubot?
|
| Előzmény: [345] öreg, 2007-08-07 12:06:35 |
|
| [346] lorantfy | 2007-08-07 15:21:36 |
 Kedves Öreg!
Köszönjük az észrevételedet! A C.900. feladat magoldása valóban nem egy szám, hanem 8 megoldás van:
216, 324, 432, 540, 648, 756, 864, 972, ahogy Te is írtad.
A szövege nem könnyű, de szerintem nem magyartalan. Persze lehetne bővíteni a szöveget, hogy könnyebben érthető legyen:
Egy különböző számjegyekből álló háromjegyű szám értékének 75 százaléka egy olyan háromjegyű szám, melyben ugyanazok a számjegyek szerepelnek mint az eredeti számban, de egyik számjegy sincs az eredeti helyén. Melyik ez a szám?
|
| Előzmény: [345] öreg, 2007-08-07 12:06:35 |
|
| [345] öreg | 2007-08-07 12:06:35 |
 Nosztalgiából megnéztem a 2007. májusi feladatokat és megoldásokat és elszomorodtam, illetve megijedtem, hogy ennyire öregszem mert két megoldást nem értek.:(
A C.900. feladatnál már a kérdéssel is bajban voltam, mert kicsit magyartalan a megfogalmazás. De a megoldásból megértettem a kérdést. Viszont miért csak a (216;162) a megoldás? A (324;234)(432;324)(540;405)(648;486)(756;567)(864;648)(972;729) miért nem elégíti ki a feltételeket?
A B.4011.-es feladatnál pedig a kiírás szerint 2007 lakója van a falunak, a megoldás pedig mintha 103 lakosra lenne megadva.
Már nagyon rég volt, de szép emlék a KÖMAL...
|
|
| [344] rizsesz | 2007-07-31 01:18:13 |
 az én problémám nem ez volt, hanem az, hogy a feladat még nem volt hozzáférhető, se az újságban, sem a neten. ellenben az illető felrakta egy honlapra azt a feladatot április akárhányadikán, ami a kömalban május 10.-e után jelent meg.
|
|
| [343] Doom | 2007-07-25 09:48:48 |
 Szerintem nagyon is tudja... Csak van, akinek elég "érdekes" a fontossági és érték-sorrendje.
Viszont a kiszivárogtatás, főleg a rendszeres szerintem sem valós probléma. Ráadásul minél hamarabb rakja ki valaki a kérdést egy fórumra, annál nagyobb az esélye, hogy egy rivális is megtalálja. Sőt, így valószínűleg csak az eredeti kirakó dolgozata lesz NVSZ, így előbb-utóbb (a picit is nagyobb tömeg csinálja ezt) rá fognak döbbeni, hogy pont az első ember szívja meg és csak másoknak segít saját maga ellen, így talán ez elég elrettentésnek, ha amúgy is csak azért csinálta, hogy ő nyerjen.
|
| Előzmény: [342] Willy, 2007-07-25 01:53:51 |
|
| [342] Willy | 2007-07-25 01:53:51 |
 Hát, csak azt nem értem, hogy az aki csal miért nem érti, hogy ezzel leginkább önmagát csapja be...
Az, meg, hogy egy feladat hogyan szivárog ki, hát engem is nagyon érdekelne... de nem hinném, hogy erről volna szó. Az már nagyon durva lenne... kb. mint az, amit Jonas írt.
|
| Előzmény: [341] rizsesz, 2007-07-24 16:44:11 |
|
| [341] rizsesz | 2007-07-24 16:44:11 |
 Szerintem annak is érdemes lenne utánajárni, hogy hogyan szivároghatott ki idő előtt a feladat. Már ha erről van szó (a jóindulat szóljon belőlem: a feladat előkerült valamilyen válogatón, szakkörön, satöbbi)... azt mindenesetre ne mesélje be nekem senki, hogy 1 hónappal a feladat megjelenése előtt ő pont ezt a feladatot rakta ki egészen véletlenül 1 fórumra, hogy oldjátok meg...
|
|
| [340] Alma | 2007-07-24 15:58:46 |
 Szerintem aki egy pontverseny feladatát kitűzi fórumon határidő lejárta előtt és aztán a saját nevével beküldi azt, az szánalmas. Aki ezt más nevében teszi a kitűzést az nem csak szánalmas hanem aljas, rosszindulatú, bunkó, tirpák, gerinctelen és undorító is. Szerintem nincs olyan kömalozó aki ilyet tenne.
|
| Előzmény: [339] jonas, 2007-07-24 11:16:44 |
|
| [339] jonas | 2007-07-24 11:16:44 |
 A legrosszabb (és nem akarok ötleteket adni), hogy elvileg más valaki is beküldhet egy versenyző nevével nem versenyszerű dolgozatokat, vagy megkérdezheti látszólag a versenyző nevében a feladatot egy internetes fórumon. Ezt úgy is meg lehet tenni, hogy gyakorlatilag lehetetlen kinyomozni.
|
|







 A
A




