Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[438] BohnerGéza	2009-02-17 22:12:34
Ha belátjuk, hogy P az ABQ körülírt körén van, a többi rész már könnyebb.

[437] S.Ákos	2009-02-17 17:15:39
Valaki tudna mutatni az A.470 feladatra egy elemi (koordinátageo nélküli) megoldást?

[436] janomo	2008-12-23 10:20:54
Ezt a jelet kétféleképpen szokták használni, valódi részhalmazként, ha külön mondják és normálisként, ha nem írnak oda semmit. Én ebben a nagy zűrzavarban a végén elfelejtettem, hogy vannaki végtelen halmazok is. Kellemes ünnepeket mindenkinek: Nagy János
Előzmény: [435] Python, 2008-12-22 19:22:52

[435] Python

2008-12-22 19:22:52

Az A.464. feladatban az " $\subset$ " jel mit akart jelenteni? Én úgy tudom, hogy ez a "valódi részhalmaz" jele (tehát ha A=B, akkor A $\subset$ B nem teljesül), de a hivatalos megoldás ezt a "részhalmaz" jelölésére használja (aminél szerintem a " $\subset$ "-et alá kellene húzni, mint az " $\le$ "-nél az "<"-t, és ami A=B esetén is igaz). Ha pedig a " $\subset$ " a valódi részhalamaz jele, akkor a feladat állítása nem igaz (legegyszerűbb példa az üres vagy az egyelemű halamaz, de minden n-re van n-elemű ellenpélda).

[434] Doky	2008-12-22 15:45:54
Ákosnak igaza van! Bár szerintem egyszerűbb volt úgy nézni mint a javítókulcs mutatja. Itt( ahogy te csináltad) több esély volt az elszámolásnak.
Előzmény: [432] Blinki Bill, 2008-12-22 09:16:59

[433] S.Ákos	2008-12-22 10:21:56
Arra nem figyeltél, hogy nem ugyanakkora a valószínűsége az eseményeknek.
Előzmény: [432] Blinki Bill, 2008-12-22 09:16:59

[432] Blinki Bill

2008-12-22 09:16:59

Kedves Fórumozók!

A C.958. számú feladatra az alábbi megoldást adtam. Kérlek, ha van egy kis időtök, akkor mondjátok meg, hogy mi a hiba benne, mert egészen más eredményt kaptam, mint a hivatalos megoldás.

Előre is kösz.

Számoljuk össze a lehetséges játék-befejeződéseket:

1dobásból vége van a játéknak: 4est dobunk, vagy 5-öst dobunk vagy 6-ost dobunk, azaz 3 eset összesen

2dobásból van vége a játéknak: 1-3;1-4;1-5;1-6; 2-2;2-3;2-4;2-5;2-6; 3-1;3-2;3-3;3-4;3-5;3-6, azaz 15 eset összesen

3dobásból van vége a játéknak: 1-1-2;1-1-3;1-1-4;1-1-5;1-1-6; 1-2-1;1-2-2;1-2-3;1-2-4;1-2-5;1-2-6; 2-1-1;2-1-2;2-1-3;2-1-4;2-1-5;2-1-6, azaz összesen 17 eset

4dobásból van vége a játéknak: 1-1-1-1;1-1-1-2;1-1-1-3;1-1-1-4;1-1-1-5;1-1-1-6, azaz összesen 6 eset

több változat nincs,mert 4pozitív szám összege legalább négy és 4 mezőre voltunk a céltól.

Amikor több,mint két dobás kell, azon esetek száma 17+6=23, az összes eseté pedig 41, tehát a keresett valószínűség 23/41.

Bogár Blanka 7.o.

[431] nadorp

2008-12-20 10:22:54

Megjegyzés az A.465. számú feladat megoldásához ( másképp számolva)

Ha 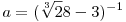$a=(\root3\of28-3)^{-1}$ ,akkor

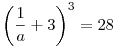$\left(\frac1a+3\right)^3=28$ , azaz "a" gyöke az

x³-27x²-9x-1=0 egyenletnek. Ha ennek az egyenletnek a másik két gyöke b és c - melyek nyilván komplex számok és egymás konjugáltjai -, akkor a megoldásban közölt S összegre

S=aⁿ+bⁿ+cⁿ

A gyökök és együtthatók összefüggése alapján

a+b+c=27

a²+b²+c²=(a+b+c)²-2(ab+ac+bc)=27²-2^.(-9)=747

Tekintsük ezek után az

x_n+3=27^.x_n+2+9^.x_n+1+x_n rekurziót a x₀=3, x₁=27, x₂=747 kezdeti értékekkel. A rekurzió karakterisztikus egyenletének gyökei éppen a,b és c, tehát

x_n=aⁿ+bⁿ+cⁿ

másrészt az x_n sorozat elemei egész számok sőt egyszerű indukcióval adódik, hogy 6k+3 alakúak. Mivel abc=1, ezért

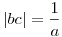
$|bc|=\frac1a$

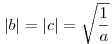$|b|=|c|=\sqrt{\frac1a}$ , azaz

$x_n=a^n+\frac2{{\sqrt a}^n}\cos n\phi$ alakú alkalmas $\phi$ értékre. Innen a>27 miatt már látszik, hogy

x_n-1<aⁿ<x_n+1, azaz [aⁿ]=x_n vagy [aⁿ]=x_n-1, tehát 6k+2 vagy 6k+3 alakú

[430] nadorp

2008-11-23 22:25:09

Most már látom mi tévesztett meg,elírtam. Helyesen:

Ha az eredeti állításs HAMIS lenne ...

Előzmény: [427] rizsesz, 2008-11-22 17:23:13

[429] Róbert Gida	2008-11-23 03:52:10
??? A segédtétel megfordítása triviális. Amúgy több is igaz. Szép megoldás.
Előzmény: [427] rizsesz, 2008-11-22 17:23:13

[428] Valezius	2008-11-22 17:26:47
Teljesen jó bizonyítás, gondold át újra :) Indirekt tegyük fel, hogy a keresett szám racionális, akkor a segédtétel miatt a 100. hatványösszeg is racionális. Ezzel megvan a kívánt ellentmondás.
Előzmény: [427] rizsesz, 2008-11-22 17:23:13

[427] rizsesz	2008-11-22 17:23:13
Na, jól megfogalmaztam - szóval a segédtétel bizonyítása jó, de a végén pont a fordított állítást használod fel.
Előzmény: [426] rizsesz, 2008-11-22 17:22:28

[426] rizsesz	2008-11-22 17:22:28
Nem jó a bizonyításod. A segédtételt legalábbis csak az egyik irányban bizonyítod be, viszont a megoldásod végén a másik irányt használod ki.
Előzmény: [425] nadorp, 2008-11-22 16:23:36

[425] nadorp

2008-11-22 16:23:36

Az alábbi megoldás kicsit egyszerűbb a közöltnél és általánosabb is

B. 4109. Igazoljuk, hogy

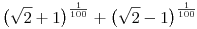
$\big(\sqrt{2}+1\big)^{\frac{1}{100}}+ \big(\sqrt{2}-1\big)^{\frac{1}{100}}$

irracionális szám.

Bebizonyítjuk a következő segédállítást:

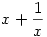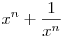Ha $x+\frac1x$ racionális, akkor $x^n+\frac1{x^n}$ is racionális minden pozitív egész n-re

Az állítás n=1 esetén nyilván igaz,n=2-re

$x^2+\frac1{x^2}=\left(x+\frac1x\right)^2-2$ miatt szintén teljesül.

Ha n>2, akkor indukcióval

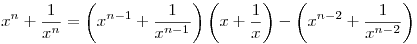
$x^n+\frac1{x^n}=\left(x^{n-1}+\frac1{x^{n-1}}\right)\left(x+\frac1x\right)-\left(x^{n-2}+\frac1{x^{n-2}}\right)$

miatt n-re is igaz a segédállítás.

Ha az eredeti feladat állítása igaz lenne, akkor a segédállításban $x=(\sqrt2+1)^{\frac1{100}}$ és n=100 értékeket véve

$(\sqrt2+1)+(\sqrt2-1)=2\sqrt2$ is racionális lenne, ami ellentmondás

[424] KK07	2008-11-19 18:48:53
Azt szeretném megtudni hogy a a C951 -s feladatnál nem volt megadva hogy melyik saroktól számolom, és én azt küldtem be ha a jobbról számolom akkor 4, de ha balról akkor 12! Ez rossznak számít? Mert sztem akkor egyértelművé kellet volna tenni!

[423] Káli gúla	2008-11-19 13:19:59
Igy lehetne "fejben" igazolni, hogy a szorzat valóban annyi, amennyi: 16656=(100+66)(100-66)=10000-66², és 66²=6²11²=30121=3630, ezért a szorzat : 10000-3630=8590 (minden szám 12-es számrendszerben van írva).

[422] Káli gúla	2008-11-19 10:35:12
Egyébként mindenféle polinomok nélkül a "kilences" próba azt adja a 16656-8590-re (1+6+6=13, 5+6=11, 8+5+9+0=22), hogy 1311-22 = 121 osztható (a-1)-gyel, tehát a=2, a=12 vagy a=122. Az alap páros, így 166*56 4-gyel osztható, ezért 8590 is, tehát a is 4-gyel osztható, vagyis a=12.
Előzmény: [421] Róbert Gida, 2008-11-19 02:01:49

[421] Róbert Gida	2008-11-19 02:01:49
A komal.hu-n közölt C950. megoldása rossz, egy érettségin sem fogadnák el. Ha történetesen f(9)=0 volna akkor sem lenne megoldás, mivel a jegyek között szerepel a 9, így a számrendszer alapja nem lehet 9. f(12)=0, de ott sem nézte meg, hogy minden számjegy kisebb-e, mint 12.

[420] Róbert Gida

2008-11-19 01:54:50

B.4413. négy potya pontért, a Maple szerint ugyanis:

factor(2*(a⁴+b⁴+c⁴+(-a-b-c)⁴)+8*a*b*c*(-a-b-c));

4*(a²+a*b+b²+a*c+b*c+c²)²

[419] KK07	2008-10-31 12:08:41
Helló mindenkinek! Nem tudná valaki fel tenni a szeptemberi megoldásokat, hogy össze vessem az enyéimmel! :) Előre is köszi, bár én nem tartozom a "nagyok közé" én még mindig csak a C kategóriával próbálkozom. Ezért elsősorban az érdekelne. :P Üdv: Kristóf

[418] Róbert Gida	2008-10-27 14:27:39
Nem oldottam meg, de a konstans éles: http://www.mathlinks.ro/viewtopic.php?p=1187185#1187185
Előzmény: [417] janomo, 2008-10-27 08:47:45

[417] janomo

2008-10-27 08:47:45

Hello!

Ha valaki tudja, örülnék, ha feltenné a tavalyi májusi A455 feladat megoldását.

N.J.

[416] lorantfy	2008-09-17 10:24:15
Nagyon tetszik! Köszönöm, hogy feltetted!
Előzmény: [406] Káli gúla, 2008-06-16 17:00:58

[415] nadorp

2008-09-10 15:26:51

A. 457.

Legyen p páratlan prímszám. Igazoljuk, hogy

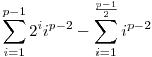
$\sum_{i=1}^{p-1}2^ii^{p-2}-\sum_{i=1}^{\frac{p-1}2}i^{p-2}$

osztható p-vel.

Azt bizonyítjuk be, hogy a mod p testben a fenti kifejezés 0, azaz a két összeg egyenlő.

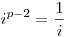Mivel 1 $\leq$ i $\leq$ p-1 esetén $i^{p-2}=\frac1i$ , ezért

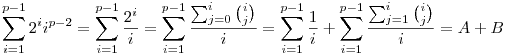
$\sum_{i=1}^{p-1}2^ii^{p-2}=\sum_{i=1}^{p-1}\frac{2^i}i=\sum_{i=1}^{p-1}\frac{ \sum_{j=0}^i\binom{i}{j}}i=\sum_{i=1}^{p-1}\frac1i+\sum_{i=1}^{p-1}\frac{\sum_{j=1}^i\binom{i}{j}}i=A+B$

Mivel 1 $\leq$ j $\leq$ i esetén

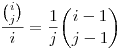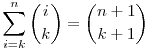$\frac{\binom{i}{j}}i=\frac1j\binom{i-1}{j-1}$ , ezért felhasználva az ismert $\sum_{i=k}^n\binom{i}{k}=\binom{n+1}{k+1}$ összefüggést

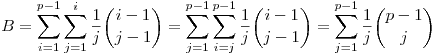
$B=\sum_{i=1}^{p-1}\sum_{j=1}^i\frac1j\binom{i-1}{j-1}=\sum_{j=1}^{p-1}\sum_{i=j}^{p-1}\frac1j\binom{i-1}{j-1}=\sum_{j=1}^{p-1}\frac1j\binom{p-1}{j}$

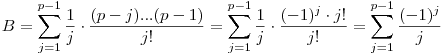$B=\sum_{j=1}^{p-1}\frac1j\cdot\frac{(p-j)...(p-1)}{j!}=\sum_{j=1}^{p-1}\frac1j\cdot\frac{(-1)^j\cdot j!}{j!}=\sum_{j=1}^{p-1}\frac{(-1)^j}j$ Tehát

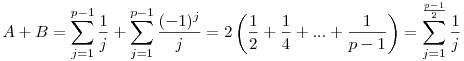
$A+B=\sum_{j=1}^{p-1}\frac1j+\sum_{j=1}^{p-1}\frac{(-1)^j}j=2\left(\frac12+\frac14+...+\frac1{p-1}\right)=\sum_{j=1}^{\frac{p-1}2}\frac1j$

és ezt kellett belátni

[414] Róbert Gida

2008-06-19 11:50:41

Akkor szerinted 24 darab 5 pontos megoldás fog érkezni a feladatra? Kizárt. Egyébként nem kell hozzá semmilyen trükk. Angolul is fent vannak a feladatok a Kömalon, csak a feladat pontos szövegére rákeresve a harmadik találat, de az első is a Putnam feladatról szól, de az fizetős cikk.

"Sajnos manapság az Internet korában sokkal nehezebb olyan feladatot kitűzni, amit nem lehet a Google-lal megoldani."

Ezért kell eredeti feladatokat kitűzni...

Előzmény: [413] jenei.attila, 2008-06-19 09:40:37

Már regisztráltál?
Új vendég vagy?