|
|
| [443] Vonka Vilmos Úr | 2009-02-21 19:12:58 |
 Tényleg igen szép a [441]-ben vázolt megoldás!
Az (ABCD) kollineáris pontnégyest harmonikusnak nevezzük, ha az (ABCD) kettősviszony -1, azaz 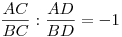 . .
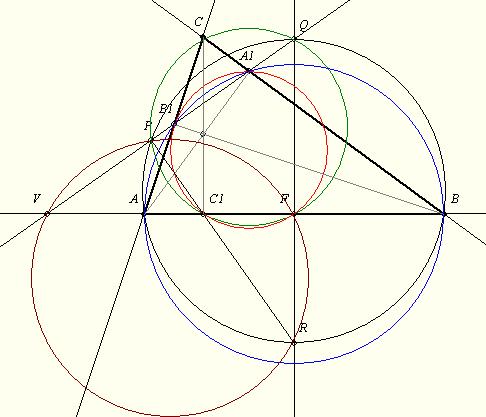
Ismert projektív geometriai tétel, hogy az (ABCD) pontnégyes pontosan akkor harmonikus, ha van olyan teljes négyszög, amelynek A és B csúcsai, C átlóspontja, D pedig a C-vel szemköztes átló metszéspontja az AB egyenessel. Ez annyit jelent, hogy (ABCD) pontosan akkor harmonikus pontnégyes, ha vannak olyan P és Q pontok, hogy a PQ egyenes az AB egyenest C-ben metszi; és az AP és BQ, valamint AQ és BP egyenesek metszéspontjait összekötő egyenes AB-t D-ben metszi. Ennek a tételnek a bizonyítása valóban a vetítéseket - és a vetítések kettősviszonytartó tulajdonságát - használja. (Lásd pl. ebben a jegyzetben az 53. oldalon.)
Így a feladatban az, hogy (ABDC1) harmonikus pontnégyes, egyszerűen onnan látható, hogy az ABA1B1 teljes négyszög átlóspontja D, a szemköztes oldalegyenes pedig AB-t C1-ben metszi.
Innen 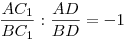 miatt az miatt az 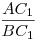 és és 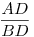 arányok valóban (előjeltől eltekintve) megegyeznek, tehát C1 és D ugyanazon az A és B által meghatározott Apollonius-körön van... a bizonyítás pedig [441] alapján befejezhető. arányok valóban (előjeltől eltekintve) megegyeznek, tehát C1 és D ugyanazon az A és B által meghatározott Apollonius-körön van... a bizonyítás pedig [441] alapján befejezhető.
|
| Előzmény: [442] BohnerGéza, 2009-02-21 15:37:00 |
|
| [442] BohnerGéza | 2009-02-21 15:37:00 |
 Örülök, ha valaki szép megoldást talál valamely feladatra!
Nekem biztosan, de talán másoknak is segítenél, ha leírnád a harmonikus pontnégyes fogalmát, de főleg a megfelelő vetítéseket. Előre köszönöm!
|
| Előzmény: [441] janomo, 2009-02-21 13:54:57 |
|
| [441] janomo | 2009-02-21 13:54:57 |
 Ez egyáltalán nem szép, elemi megoldás. Sokkal egyszerűbben látható a feladat, ha azt igazoljuk, hogy a PC1 egyenes szögfelező az APB háromszögbenEbből könnyen következik az, hogy A, B, P, Q egy körön vannak.
Azt, hogy az említett egyenes szögfelező, az appolonius körrel láthatjuk, be, ugyanis az A1B1 és az AB egyenes metszéspontja D, akkor vetítésekkel egyszerűen látható, hogy D, A, C1 és B harmonikus pontnégyest alkotnak.
Ekkor D rajta van az appolonius körön és C1 is és ráadásul az appolonis kör szimmetrikus az AB egyenesre, amiből az Appolonius kör a DC1 szakasz Thaleszköre, viszont ezen rajta van P is, mivel a DPC1 szög 90 fok. Ezzel készen vagyunk. Ehhez a bizonyításhoz egyáltalán nem kell számolni
|
| Előzmény: [440] BohnerGéza, 2009-02-21 04:33:29 |
|
|
|
| [438] BohnerGéza | 2009-02-17 22:12:34 |
 Ha belátjuk, hogy P az ABQ körülírt körén van, a többi rész már könnyebb.
|
|
| [437] S.Ákos | 2009-02-17 17:15:39 |
 Valaki tudna mutatni az A.470 feladatra egy elemi (koordinátageo nélküli) megoldást?
|
|
| [436] janomo | 2008-12-23 10:20:54 |
 Ezt a jelet kétféleképpen szokták használni, valódi részhalmazként, ha külön mondják és normálisként, ha nem írnak oda semmit. Én ebben a nagy zűrzavarban a végén elfelejtettem, hogy vannaki végtelen halmazok is. Kellemes ünnepeket mindenkinek: Nagy János
|
| Előzmény: [435] Python, 2008-12-22 19:22:52 |
|
|
|
|
| [432] Blinki Bill | 2008-12-22 09:16:59 |
 Kedves Fórumozók!
A C.958. számú feladatra az alábbi megoldást adtam. Kérlek, ha van egy kis időtök, akkor mondjátok meg, hogy mi a hiba benne, mert egészen más eredményt kaptam, mint a hivatalos megoldás.
Előre is kösz.
Számoljuk össze a lehetséges játék-befejeződéseket:
1dobásból vége van a játéknak: 4est dobunk, vagy 5-öst dobunk vagy 6-ost dobunk, azaz 3 eset összesen
2dobásból van vége a játéknak: 1-3;1-4;1-5;1-6; 2-2;2-3;2-4;2-5;2-6; 3-1;3-2;3-3;3-4;3-5;3-6, azaz 15 eset összesen
3dobásból van vége a játéknak: 1-1-2;1-1-3;1-1-4;1-1-5;1-1-6; 1-2-1;1-2-2;1-2-3;1-2-4;1-2-5;1-2-6; 2-1-1;2-1-2;2-1-3;2-1-4;2-1-5;2-1-6, azaz összesen 17 eset
4dobásból van vége a játéknak: 1-1-1-1;1-1-1-2;1-1-1-3;1-1-1-4;1-1-1-5;1-1-1-6, azaz összesen 6 eset
több változat nincs,mert 4pozitív szám összege legalább négy és 4 mezőre voltunk a céltól.
Amikor több,mint két dobás kell, azon esetek száma 17+6=23, az összes eseté pedig 41, tehát a keresett valószínűség 23/41.
Bogár Blanka 7.o.
|
|
| [431] nadorp | 2008-12-20 10:22:54 |
 Megjegyzés az A.465. számú feladat megoldásához ( másképp számolva)
Ha 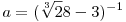 ,akkor ,akkor
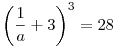 , azaz "a" gyöke az , azaz "a" gyöke az
x3-27x2-9x-1=0 egyenletnek. Ha ennek az egyenletnek a másik két gyöke b és c - melyek nyilván komplex számok és egymás konjugáltjai -, akkor a megoldásban közölt S összegre
S=an+bn+cn
A gyökök és együtthatók összefüggése alapján
a+b+c=27
a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=272-2.(-9)=747
Tekintsük ezek után az
xn+3=27.xn+2+9.xn+1+xn rekurziót a x0=3, x1=27, x2=747 kezdeti értékekkel. A rekurzió karakterisztikus egyenletének gyökei éppen a,b és c, tehát
xn=an+bn+cn
másrészt az xn sorozat elemei egész számok sőt egyszerű indukcióval adódik, hogy 6k+3 alakúak. Mivel abc=1, ezért
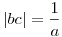
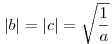 , azaz , azaz
 alakú alkalmas alakú alkalmas  értékre. Innen a>27 miatt már látszik, hogy értékre. Innen a>27 miatt már látszik, hogy
xn-1<an<xn+1, azaz [an]=xn vagy [an]=xn-1, tehát 6k+2 vagy 6k+3 alakú
|
|
|
|
| [428] Valezius | 2008-11-22 17:26:47 |
 Teljesen jó bizonyítás, gondold át újra :) Indirekt tegyük fel, hogy a keresett szám racionális, akkor a segédtétel miatt a 100. hatványösszeg is racionális. Ezzel megvan a kívánt ellentmondás.
|
| Előzmény: [427] rizsesz, 2008-11-22 17:23:13 |
|
|
|
| [425] nadorp | 2008-11-22 16:23:36 |
 Az alábbi megoldás kicsit egyszerűbb a közöltnél és általánosabb is
B. 4109. Igazoljuk, hogy
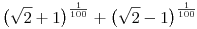
irracionális szám.
Bebizonyítjuk a következő segédállítást:
Ha 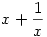 racionális, akkor racionális, akkor 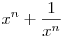 is racionális minden pozitív egész n-re is racionális minden pozitív egész n-re
Az állítás n=1 esetén nyilván igaz,n=2-re
 miatt szintén teljesül. miatt szintén teljesül.
Ha n>2, akkor indukcióval
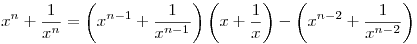
miatt n-re is igaz a segédállítás.
Ha az eredeti feladat állítása igaz lenne, akkor a segédállításban  és n=100 értékeket véve és n=100 értékeket véve
 is racionális lenne, ami ellentmondás is racionális lenne, ami ellentmondás
|
|
| [424] KK07 | 2008-11-19 18:48:53 |
 Azt szeretném megtudni hogy a a C951 -s feladatnál nem volt megadva hogy melyik saroktól számolom, és én azt küldtem be ha a jobbról számolom akkor 4, de ha balról akkor 12! Ez rossznak számít? Mert sztem akkor egyértelművé kellet volna tenni!
|
|
| [423] Káli gúla | 2008-11-19 13:19:59 |
 Igy lehetne "fejben" igazolni, hogy a szorzat valóban annyi, amennyi: 166*56=(100+66)*(100-66)=10000-662, és 662=62*112=30*121=3630, ezért a szorzat : 10000-3630=8590 (minden szám 12-es számrendszerben van írva).
|
|
| [422] Káli gúla | 2008-11-19 10:35:12 |
 Egyébként mindenféle polinomok nélkül a "kilences" próba azt adja a 166*56-8590-re (1+6+6=13, 5+6=11, 8+5+9+0=22), hogy 13*11-22 = 121 osztható (a-1)-gyel, tehát a=2, a=12 vagy a=122. Az alap páros, így 166*56 4-gyel osztható, ezért 8590 is, tehát a is 4-gyel osztható, vagyis a=12.
|
| Előzmény: [421] Róbert Gida, 2008-11-19 02:01:49 |
|
| [421] Róbert Gida | 2008-11-19 02:01:49 |
 A komal.hu-n közölt C950. megoldása rossz, egy érettségin sem fogadnák el. Ha történetesen f(9)=0 volna akkor sem lenne megoldás, mivel a jegyek között szerepel a 9, így a számrendszer alapja nem lehet 9. f(12)=0, de ott sem nézte meg, hogy minden számjegy kisebb-e, mint 12.
|
|









 " jel mit akart jelenteni? Én úgy tudom, hogy ez a "valódi részhalmaz" jele (tehát ha A=B, akkor A
" jel mit akart jelenteni? Én úgy tudom, hogy ez a "valódi részhalmaz" jele (tehát ha A=B, akkor A "-nél az "<"-t, és ami A=B esetén is igaz). Ha pedig a "
"-nél az "<"-t, és ami A=B esetén is igaz). Ha pedig a " értékre. Innen a>27 miatt már látszik, hogy
értékre. Innen a>27 miatt már látszik, hogy 

