|
|
|
| [505] Tibixe | 2010-01-12 20:06:28 |
 Az A496 megoldása megvan valakinek?
( nekem csak k 5 esetben ) 5 esetben )
|
|
|
| [503] S.Ákos | 2010-01-12 14:00:47 |
 A.495.-re tudna valaki mutatni megoldást? Köszönöm előre is. S.Á.
|
|
| [502] HoA | 2010-01-03 21:51:50 |
 Elegánsabb, ha elhagyjuk az R és T merőleges vetületeket. Jelöljük P1P4 és P3O metszéspontját U-val. S-et mint P1P4 és a P2-n át P3O-val húzott párhuzamos metszéspontját definiáljuk. Ekkor a P2P3US paralellogrammában SU=P2P3=b .
P1P4=1=P1Q-QS+SU+UP4=b-b3+b+b=3b-b3
|
| Előzmény: [500] HoA, 2010-01-03 16:54:49 |
|
| [501] zotyo58 | 2010-01-03 19:19:36 |
 A 2009 emelt szintű 7/II/6.b szerintem helyesen így szólna Az f(x) függvény a téglalap esetén a ]0;9[ nyílt intervallumban értelmezett.
Az eredeti megoldása végtelen lenne, hiszen teljesül az origóra az összes feltétel, így a téglalap egyik oldala a [0;9] az x tengelyen, a másik két oldal az y tengely és az x=9 egyenes, a negyedik oldal eltávolodhat a végtelenbe...
Számomra ez volt a megoldás... Tudom általában értelemszerű a megoldás, de miért ne lehetne így is gondolkozni.
|
|
| [500] HoA | 2010-01-03 16:54:49 |
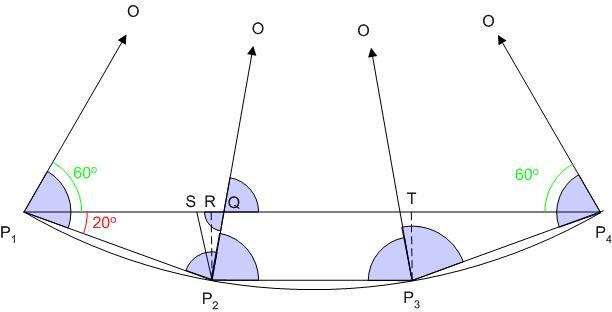
 Szemléletesebb megoldás a B. 4221. feladatra: ( Mutassuk meg, hogy ha az r sugarú körbe írt szabályos 18-szög oldala a, akkor a3+r3=3ar2. )
Legyen az egységsugarú körbe írt szabályos 18-szög oldala b, ekkor azt kell igazolni, hogy b3+1=3b. Ebben a körben a b hosszúságú húrhoz 10o kerületi és 20o középponti szög tartozik. Tekintsük a sokszög O középpontját és egymás utáni P1,P2,P3,P4 csúcsait. A P1P4 húrhoz 60oos középponti szög tartozik, P1OP4 szabályos, P1P4=1. A P1P2O=H0 20o csúcsszögű egyenlőszárú szabályos, P1P4=1. A P1P2O=H0 20o csúcsszögű egyenlőszárú  -ben az alap és a szár aránya b/1 = b. H0-lal egybevágó a P2P3O és a P3P4O háromszög. P2P1P4 -ben az alap és a szár aránya b/1 = b. H0-lal egybevágó a P2P3O és a P3P4O háromszög. P2P1P4 =20o, mint a P2P4 ívhez tartozó kerületi szög. P2O és P1P4 metszéspontja Q, P1P4 és P2P3 párhuzamossága miatt P2O és P1P4 80o –os szöget zár be, így a H1=P2QP1 =20o, mint a P2P4 ívhez tartozó kerületi szög. P2O és P1P4 metszéspontja Q, P1P4 és P2P3 párhuzamossága miatt P2O és P1P4 80o –os szöget zár be, így a H1=P2QP1 hasonló H0-hoz, P1Q=b, P2Q=b2. Legyen P2 merőleges vetülete P1P4-re R, Q tükörképe R-re S. A H2=QSP2 hasonló H0-hoz, P1Q=b, P2Q=b2. Legyen P2 merőleges vetülete P1P4-re R, Q tükörképe R-re S. A H2=QSP2 is hasonló H1-hez, QS=b3, QR=b3/2 . P1R=b–b3/2. Legyen P3 merőleges vetülete P1P4-re T. Hasonlóan adódik, hogy P4T=b–b3/2. A P2P3TR téglalapban RT=P2P3=b. is hasonló H1-hez, QS=b3, QR=b3/2 . P1R=b–b3/2. Legyen P3 merőleges vetülete P1P4-re T. Hasonlóan adódik, hogy P4T=b–b3/2. A P2P3TR téglalapban RT=P2P3=b.
P1P4=1=P1R+RT+TP4=(b–b3/2)+b+(b–b3/2)=3b–b3 .
|
 |
|
| [499] Radián | 2009-12-12 16:55:03 |
 A beküldési határidő LEJÁRT.
underbraceabcd
Ezt találtam a B. 4212-es feladat megoldásánál. Ez mit akar jelenteni?
|
|
| [498] Nandor | 2009-12-08 22:09:23 |
 B.4207
Ez a feladat ugy erzem hibasan volt megfogalmazva. Ki kellett volna kotni hogy a sokszog nem haromszog. Enelkul a megoldas tul egyszeru hiszen egy haromszog nyilvanvalo ellenpelda.
|
|
| [497] R.R King | 2009-12-06 20:23:11 |
 Az egyenletek amiket felírtál igazából egyenlőtlenségek. Bizonyítani kellene, hogy a maximumot akkor kapjuk, hogy ha az egyenlőtlenség egyenlőséggel teljesül..Bár nem vagyok javító, de erre a megoldásra szerintem nem kapsz teljes értékű pontszámot még akkor se ha történetesen ez a jó végeredmény...
|
| Előzmény: [496] Nánási József, 2009-12-06 19:04:24 |
|
| [496] Nánási József | 2009-12-06 19:04:24 |
 C.103-as feladat.
Erre adtam le megoldást:
p-papíráru
v-vegyiáru
v+3p=12
v+p=5
Fejezzük ki p-t:
p=3,5
v=1,5
Kereslet maximuma:
p*200000+v*100000=700000Ft+150000Ft=850000Ft
Azt szeretném megkérdezni, szerintetek mennyi az erre megfelelő pontszám.
Előre is ksüözönöm Józsi
|
|
|
|
| [493] Csimby | 2009-11-26 15:09:51 |
 Ellenpélda: legyen b=6 és p=7.
b2 1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül. 1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül.
A modulo p maradékosztályok a 0-t kivéve a szorzásra nézve p-1 rendű csoportot alkotnak. És csak annyit állíthatunk, hogy minden elem rendje osztja a csoport rendjét. Tehát b2 1(mod p)-ből csak az következik, hogy p páratlan. 1(mod p)-ből csak az következik, hogy p páratlan.
|
| Előzmény: [492] bily71, 2009-11-26 09:57:26 |
|
|
| [491] bily71 | 2009-11-26 09:46:20 |
 És most jöjjön egy másik lehetséges megoldás a B.4026. feladatra:
Minden p>3 prim felírható p=6k 1alakban. 1alakban.
A binomiális tétel értelmében
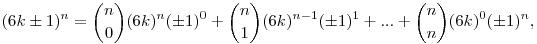
ahol a jobb oldali összeg utolsó tagja
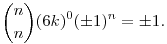
Mivel az összeg minden tagja az utolsó kivételével osztható 6-tal, ezért
(6k )n )n  1(mod 6). 1(mod 6).
Tételezzük fel indirekt módón, hogy a
pk+pm=a2
egyenlőség teljesül, ahol a pozitív egész, mivel négyzetszámon egy egész szám második hatványát értjük.
1. eset: 0<k m, és k és m paritása megegyezik. Ebben az esetben m, és k és m paritása megegyezik. Ebben az esetben
a2  2(mod 6), 2(mod 6),
de ez csak úgy lehetséges, ha az
a2  2(mod 3) 2(mod 3)
kongruencia is teljesül. Ez pedig nem teljesülhet, mert az Euler-Fermat-tétel miatt
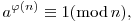
ha a és n relatív prímek, és mivel  (3)=2, ezért, ha 3 (3)=2, ezért, ha 3|a, akkor a2 1(mod 3), ha pedig 3|a, akkor a2 1(mod 3), ha pedig 3|a, akkor a2 0(mod 3), így az a2 0(mod 3), így az a2  2(mod 3) kongruencia nem teljesülhet. 2(mod 3) kongruencia nem teljesülhet.
2. eset: 0<k<m, és k és m paritása ellentétes. Ekkor
pk+pm=pm(pk-m+1)
pm(pk-m+1)=a2,
ez csak úgy lehetséges, ha 2|m. Osszunk le pm-mel, legyen 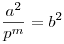 , és k-m=x, ekkor , és k-m=x, ekkor
px+1=b2.
Mivel px  1(mod 3), ezért vagy a b2 1(mod 3), ezért vagy a b2 2(mod 3), vagy a b2 2(mod 3), vagy a b2 0(mod 3) kongruencia teljesül. Az előbbi nem teljesülhet az 1.-ben tárgyaltak miatt. Nézzük az utóbbit: 0(mod 3) kongruencia teljesül. Az előbbi nem teljesülhet az 1.-ben tárgyaltak miatt. Nézzük az utóbbit:
px+1 1(mod p), 1(mod p),
ebből következik, hogy
b2 1(mod p). 1(mod p).
Ez viszont azt jelentené, mivel az Euler-Ferma-tétel megfordítása is igaz, hogy p=3, vagy 3|p, de egyik sem lehetséges, mert a feladat szerint p>3 és p P, azaz prím. P, azaz prím.
3. eset: k=m=0, ekkor a2 2(mod 3), mivel pk=pm=1, de ez a kongruencia nem teljesülhet az 1.-ben részletezett okok miatt. Több lehetőség nincs. 2(mod 3), mivel pk=pm=1, de ez a kongruencia nem teljesülhet az 1.-ben részletezett okok miatt. Több lehetőség nincs.
|
|
| [490] R.R King | 2009-11-24 18:42:27 |
 Szerintem nem kell aggódnod, mert már most többet tudsz, mint a felvételizők többsége:) Hidd el sokat változott a színvonal 20 év alatt. A másik topicban tett hibás gondolatmeneteidről meg annyit, hogy ki tudja, talán egyszer valaki hasonló nyomon indulva bizonyít be valamit a láncszemeket megfelelően helyretéve.. Vajon hány tétel született úgy, hogy előtte 100 rossz utat végigjárt a megoldó??? A legtöbben pedig, akik bírálnak 2-3 matektanártól tanulták amit tudnak, önállóan még nem sokat tettek le az asztalra..Akinek nem inge, ne vegye magára.
|
| Előzmény: [489] bily71, 2009-11-24 17:52:53 |
|
| [489] bily71 | 2009-11-24 17:52:53 |
 Nemcsak szerencsésebb, hanem helyesebb is. Amit én írtam, csak k=2 esetén lehet igaz. Hirtelen nem is jutott eszembe, hogy k bármilyen egész lehet, annyira a négyzetszámokra koncentráltam. Azt hiszem, nem lesz egyszerű visszaülni 20 év után az iskolapadba, egy kicsit össze kell szednem magam, hogy sikerüljön a felvételi:)
|
| Előzmény: [488] R.R King, 2009-11-24 16:46:04 |
|
| [488] R.R King | 2009-11-24 16:46:04 |
 A 3. rész végén talán szerencsésebb azt mondani, egy prímhatvány csak úgy bontható egészek szorzatára, ha a tényezők maguk is ugyanannak a prímnek a hatványai. Jelen esetben a a+1 és a-1 különbsége 2, így ezek nem lehetnek, mert p>3, még az sem lehet hogy az egyik tényező 1 a másik pedig maga p a k-on(leellenőrizhető!)
|
| Előzmény: [487] bily71, 2009-11-24 16:00:25 |
|
| [487] bily71 | 2009-11-24 16:00:25 |
 Sokan bírálták (jogosan) eddigi működésemet, ezért jöjjön egy lehetséges megoldás egy, a tudásszintemhez méretezett feladatra:
B.4026. Legyen p>3 prímszám, k és m pedig nemnegatív egész számok. Igazoljuk, hogy pk+pm nem lehet négyzetszám.
Megoldás:
pk+pm=a2, ahol a nemnegatív egész, ugyanis négyzetszám definició szerint csak egy egész szám második hatványa lehet. Négy eset lehetséges:
1. k=m=0, ekkor
pk=pm=1
pk+pm=2
2=a2
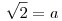 , ,
ami nem lehet, mert a a feladat szerint egész.
2. k=m>0, ekkor
pk=pm
pk+pm=2pm
2pm=a2,
ami nem lehet, mert egy négyzetszám prímtényezős felbontásában minden hatványkitevő páros, a baloldali 2-es kitevője pedig páratlan.
3. k>m=0, ekkor
pm=1
pk+pm=pk+1
pk+1=a2
pk=a2-1
pk=(a+1)(a-1),
ami nem lehet, mert (a+1) (a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám. (a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám.
4. k>m>0, ekkor
pk+pm=pm(pk-m+1)
pm(pk-m+1)=a2,
ami csak úgy lehetséges, ha 2|m, osszuk le az egyenletet pm-el. Legyen 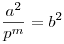 , és k-m=x, b és x nemnegatív egészek, ekkor , és k-m=x, b és x nemnegatív egészek, ekkor
px+1=b2
px=b2-1
px=(b+1)(b-1),
ez pedig nem lehet a 3. esetnél részletezett okok miatt. Több lehetőség nincs.
|
|
|
|
|





 5 esetben )
5 esetben )


 szabályos, P1P4=1. A P1P2O=H0 20o csúcsszögű egyenlőszárú
szabályos, P1P4=1. A P1P2O=H0 20o csúcsszögű egyenlőszárú  =20o, mint a P2P4 ívhez tartozó kerületi szög. P2O és P1P4 metszéspontja Q, P1P4 és P2P3 párhuzamossága miatt P2O és P1P4 80o –os szöget zár be, így a H1=P2QP1
=20o, mint a P2P4 ívhez tartozó kerületi szög. P2O és P1P4 metszéspontja Q, P1P4 és P2P3 párhuzamossága miatt P2O és P1P4 80o –os szöget zár be, így a H1=P2QP1



 1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül.
1 (mod p) nagyon-nagyon-nagyon nem csak p=3 esetén teljesül.  1alakban.
1alakban.  (3)=2, ezért, ha 3
(3)=2, ezért, ha 3 P, azaz prím.
P, azaz prím.  (a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám.
(a-1), és egy prímhatvány szorzótényezős felbontásában nem szerepelhet két különböző szám.