|
| [537] R.R King | 2010-04-19 20:01:18 |
 Pontosan erre gondoltam az előző hozzászólásban csak nem volt konkrét ellenpéldám
|
|
|
| [535] R.R King | 2010-04-19 19:58:44 |
 Üdv. Az oszthatóságok rendben vannak, szerintem ott a hiba amikor n-et kifejezed c,d-vel, mert ott már nem mindegy, hogy a +- közül melyik valósul meg ténylegesen.
|
| Előzmény: [534] bily71, 2010-04-19 19:39:38 |
|
|
|
|
|
| [530] D. Tamás | 2010-04-19 16:36:25 |
 A megoldásomban leírtam, hogy legyen (1) 2n+1="anégyzet" és (2) 3n+1="bnégyzet" ahol a és b pozitív egész számok. Namost mi az "anégyzet"+"bnégyzet"+1 értékét akarjuk meghatározni. Ha az (1) egyenlet háromszorosából kivonjuk a (2) egyenlet 2szeresét, akkor az pont előnyünkre válik, hiszen n mint változó kiesik. Innen pedig már szerintem könnyű a feladat, ezt a kis trükköt kellett volna észrevenni, hiszen ekkor 5n+3 felbomlik 2 egész szám szorzatára. (Bár nem írom már le ide, de még azt az esetet kellett vizsgálni, hogy mi van abban az esetben, ha az egyik tényező 1. Ekkor ugye lehet 5n+3 prím is, de itt is ellentmondásra jutunk, tehát nincsen ilyen lehetőség. Bár még nem javították ki a feladatot, de remélem nem hibáztam el semmit sem.
|
|
| [529] rizsesz | 2010-04-19 16:12:16 |
 Mivel osztható egyébként 5n+3, vagy hogy jön ki az, hogy összetett szám? :) Nekem mindenféle drámai fordulat kijött n-re (a 40-gyel oszthatóság biztosan, de mintha fokozódott volna a hangulat...)
|
| Előzmény: [528] D. Tamás, 2010-04-19 15:34:38 |
|
| [528] D. Tamás | 2010-04-19 15:34:38 |
 Nem olvastam végig, de az (iii)-től kezdve lesz a gondolatmenetben a hiba. Talán túlságosan is "túlbonyolítod" ezt a feladatot (Persze ez csak az én véleményem), létezik ennél sokkal egyszerűbb megoldása is, csak egy kicsit trükközni kell.
|
|
|
| [526] bily71 | 2010-04-19 14:33:10 |
 B.4255.
2n+1 és 3n+1 négyzetszámok, ezért felírhatók a következő alakban:
2n+1=(2a 1)2=2(2a2 1)2=2(2a2 2a)+1 és 3n+1=(3b 2a)+1 és 3n+1=(3b 1)2=3(3b2 1)2=3(3b2 2b)+1. 2b)+1.
(i) n=2a2 2a=3b2 2a=3b2 2b, átrendezés után 2(a2 2b, átrendezés után 2(a2 a a b)=3b2, minden változó pozitív egész, ezért 3|(a2 b)=3b2, minden változó pozitív egész, ezért 3|(a2 a a b). b).
(ii) 2n=2a2 2a+3b2 2a+3b2 2b=2(a2 2b=2(a2 a a b)+3b2, minden változó pozitív egész, ezért 2|b2. b)+3b2, minden változó pozitív egész, ezért 2|b2.
(iii) Legyen b2/2=c és a2 a a b=3d, ekkor n=3c+3d=3(c+d). b=3d, ekkor n=3c+3d=3(c+d).
Legyen 5n+3=p, behelyettesítéssel kapjuk, hogy 5.3(c+d)+3=p, vagyis 3(5(c+d)+1)=p. A bal oldal osztható 3-mal és minden változó pozitív egész, ezért 3|p, vagyis p összetett.
|
|
|
| [524] Róbert Gida | 2010-04-14 22:03:59 |
 Pontosan nem ismerjük, az egyetlen ismert nemtrivi klasszikus Ramsey szám hipergráfokra az r3(4,4)=13. Felső becslésként a feladatra, bár lehet, hogy ismernek jobbat is, ezt kaptam: (r2 helyett r-et írok a gráfos Ramsey számoknál).
r(5,11) r(4,11)+r(5,10) r(4,11)+r(5,10) 191+442=633 191+442=633
r(5,12) r(4,12)+r(5,11) r(4,12)+r(5,11) 238+633=871 238+633=871
r(5,13) r(4,13)+r(5,12) r(4,13)+r(5,12) 291+871=1162 291+871=1162
r3(4,5) r(r3(3,5),r3(4,4))+1=r(5,13)+1 r(r3(3,5),r3(4,4))+1=r(5,13)+1 1162+1=1163 1162+1=1163
Azaz már 1163-ra is igaz, 11000 helyett. Bár ez a számolás használja a fenti ismert Ramsey számot, és 4 nemtrivi felső becslést a sima Ramsey számokra, lásd például itt
http://www.emis.de/journals/EJC/Surveys/ds1.pdf
|
| Előzmény: [521] m2mm, 2010-04-14 20:30:31 |
|
|
| [522] Tibixe | 2010-04-14 21:39:01 |
 Én konkrétan nem láttam olyan ,,versenyzőt'' aki ebben NEM ismerte fel a Ramsey-tételt még jóval azelőtt hogy nekiállt volna ,,józan ésszel''.
Persze ez csak 4-5 fős minta, de ennél nem sokkal többen küldik az A pontversenyt.
|
| Előzmény: [520] vogel, 2010-04-14 18:17:27 |
|
|
| [520] vogel | 2010-04-14 18:17:27 |
 Csak éppen a versenyzők 90 százalékának eszébe nem jut a Ramsey-szám, mert még nem is hallott erről. Inkább megpróbálja józan ésszel. Nem az egyetemi tananyaghoz kéne mérni a dolgot. Mondjuk aki A-t csinál, az már tájékozottabb lehet.
|
| Előzmény: [519] Róbert Gida, 2010-04-14 17:07:58 |
|
| [519] Róbert Gida | 2010-04-14 17:07:58 |
 A504-es feladat egy sorban következik a halálismert Ramsey tételből. Ennyire potya A feladatot régen láttam.
Ugyanebben a számban a B4257. feladat pedig tulajdonképpen egy konkrét hipergráfos Ramsey szám becslését kéri (5 pontért) r3(4,5) 11000 11000
|
|
| [518] Maga Péter | 2010-03-13 10:31:59 |
 Tegnap este végiggondoltam. Szóval legyen p>3 prím. Ekkor
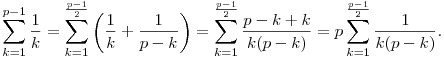
Tehát itt elegendő, hogy a 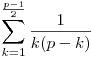 számlálója osztható p-vel, nevezője pedig nem (a közös nevezőre hozás és egyszerűsítés után). Ezt számoljuk mod p: számlálója osztható p-vel, nevezője pedig nem (a közös nevezőre hozás és egyszerűsítés után). Ezt számoljuk mod p:
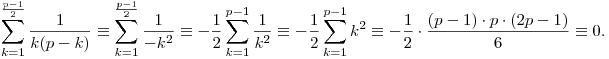
A 6 miatt nem megy ugyanez p=3-ra, p=2-re pedig már az első lépésben használt párosítás sem működik
|
| Előzmény: [515] Maga Péter, 2010-03-12 13:47:26 |
|
| [517] Tibixe | 2010-03-12 19:01:30 |
 Erről a tételről nem is tudtam
( Wikipedián alig mutat oda link, biztos azért :) ).
|
|
| [516] Róbert Gida | 2010-03-12 14:20:13 |
 Tényleg, wikin is fent van. Ezzel kb. 2 perc munka megoldani az A feladatot. De a 4-edik jegyre még mindig nem látom a bizonyítást, azaz hogy miért lenne: 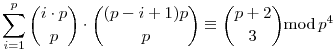 , ha p>5 prím. (Ez p=2,3,5-re nem igaz.) , ha p>5 prím. (Ez p=2,3,5-re nem igaz.)
|
| Előzmény: [515] Maga Péter, 2010-03-12 13:47:26 |
|
| [515] Maga Péter | 2010-03-12 13:47:26 |
 Az 0, ha p>3. Ha jol emlekszem Wolstenholme-tetel neven fut, bar annyira azert nem nehez. Most nem gondoltam pontosan vegig, de a p>3 feltetel ott jon be, hogy amikor az elso p-s primtenyezot kinyered, akkor utana at tudod pofozni az elso nehany szam negyzetosszegeve (talan p-1), es akkor van egy 6-os a nevezoben, ami p=2,3-ra elrontja a dolgot.
|
| Előzmény: [513] Tibixe, 2010-03-11 23:05:16 |
|
| [514] Róbert Gida | 2010-03-12 00:08:54 |
 Ennyire azért nem foglalkoztam vele, csak egy soros programot írtam rá, hogy megnézzem, hogy a többi jegy hogyan alakul.
Amit te kérsz feladatként az viszont a Válogatott feladatok és tételek az elemi matematika köréből (Aritmetika és algebra) című könyvének 60.a feladata, ami egyébként dupla csillagos, megoldása a könyv végén. Pont ennek a megoldásának az ötletét használtam az én időmben egy hasonló A feladat megoldásához.
|
| Előzmény: [513] Tibixe, 2010-03-11 23:05:16 |
|




 a
a
 1139).
1139).
