|
| [583] SAMBUCA | 2010-10-16 15:37:46 |
 Egy szép ábra, bizonyítás nélkül:
|
 |
|
|
| [581] Róbert Gida | 2010-10-14 18:55:44 |
 (lejárt) A512. feladat a méréssorozat előre kiválasztása nélkül a Válogatott feladatok és tételek az elemi matematika köréből aritmetika és algebra könyv dupla csillagos 6. feladata (általános eset bizonyítása a könyv végén). Potya példa.
Versenykiírásból: "Szép, érdekes és nem közismert feladatokat javasolhatnak kitűzésre." Kellett vagy fél métert nyúlnom az asztalon a könyvért...
|
|
|
|
| [577] Maga Péter | 2010-10-13 09:36:25 |
 Igen, azt akarták. Az én javaslatom a feladat, és én:) még odaírtam, hogy a főegyüttható ne legyen p-vel osztható. Aztán hogy, hogy nem, ez a feltétel lemaradt... De ha jól tudom, megjelenik a következő számban helyesen, és a leadási határidő egy hónappal eltolódik. Magától értetődő, hogy a px3+x megoldást nem fogják elfogadni.
|
| Előzmény: [576] Róbert Gida, 2010-10-13 01:02:53 |
|
|
| [575] Tibixe | 2010-10-12 22:51:56 |
 Az A.513 nem sikerült túl könnyűre?
( triviális megoldás: legyen f(x)=px3+x )
|
|
| [574] Róbert Gida | 2010-10-12 20:09:03 |
 Guinness világrekord, legrövidebb Kömal példamegoldás (K255):
0
|
|
|
| [572] Erben Péter | 2010-07-29 19:22:13 |
 Jelölés: 
y12-y6-2y4-1 = 2y3-2y7+2y
y12+2y7 -y6-1-2y4-2y3-2y=0
y12+2y7+y2-y2-y6-1-2y4-2y3-2y=0
(y12+2y7+y2)-(y6+y2+1+2y4+2y3+2y)=0
(y6+y)2-(y3+y+1)2=0
(y6-y3-1)(y6+y3+2y+1)=0
A második tényező pozitív, az első y3-ben másodfokú. Nemnegatív megoldása:
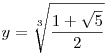
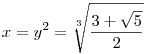
|
| Előzmény: [571] Blord, 2010-07-29 16:52:43 |
|
| [571] Blord | 2010-07-29 16:52:43 |
 Sziasztok!
Nekem sem igazán ment a 4275, én is nagyon hálás lennék egy megoldás(vázlat)ért. Valószínűleg rossz úton jártam, úgy kezdtem, hogy (gyök x)=a helyettesítés után a két oldalt négyzetre emeltem, a négyzet-b négyzet=(a-b)*(a+b), majd kis maple használat után még tovább alakítottam szorzattá, de ez az eljárás nagyon nem tetszett..
|
|
| [570] rizsesz | 2010-07-25 15:37:03 |
 Remélem jó irány :) ha kijön, kérlek szólj :) egy Bukarestbe tartó 4 órás buszút 3,5. órája környékén vettem elő és ki is jött a (2;3), (-1;1), (-1;0), de lehet, hogy van más megoldás is, azóta sem számoltam végig :)
|
| Előzmény: [569] Blinki Bill, 2010-07-25 13:17:12 |
|
|
| [568] rizsesz | 2010-07-25 11:34:04 |
 A 4277.-ben alakítsd át úgy a kifejezéseket, hogy minden x+y és x*y-nal kifejezve szerepeljen (nem egy nagy kaland) :)
utána használd fel a számtani-mértani közepek közötti összefüggést, majd átalakítások után kapsz egy felső korlátot x*y-ra (kijön, h legfeljebb 9).
ez akkor jó, ha x és y pozitív.
ha mindkettő negatív, akkor nincsen megoldás.
ha az egy negatív, a másik pozitív, akkor pedig helyettesítsd az egyiket a negatív előjelű értékkel (pl -y-nal); kicsit átalakul az egyenlet; onnan pedig zongorázd végig a legfelül leírtakat.
|
| Előzmény: [567] Blinki Bill, 2010-07-25 09:59:52 |
|
| [567] Blinki Bill | 2010-07-25 09:59:52 |
 Feltenné valaki a B.4275. és a B.4277. feladatok megoldási vázlatát, esetleg egy indító ötletet? Köszönöm.
|
|
| [566] Róbert Gida | 2010-07-15 15:19:41 |
 "Hacsak az A504 nem,[519]hsz. :DDD"
Nem, az A506-ot 12-en oldották meg teljesen (5 pontosra), míg az A504-et 6-an. Egyébként az A jelű pontversenyben a tanévben 21 diáknak van pozitív pontszáma és mindössze 7-en vannak a Fazekasból. Ez azért nem sok.
Pozitívum viszont, hogy lánygimnázium is van az A pontversenyben, de oda fiú hogyan járhat?
|
| Előzmény: [541] Blinki Bill, 2010-05-12 18:40:22 |
|
|
| [564] S.Ákos | 2010-06-16 18:20:41 |
 a0=0 sorozatot nézzük, 7|a2 és 5.17|a3, illetve maradékokkal látható, hogy a6-nak van ezektől különböző prímosztója, mivel mindegyik 1. hatványon szerepel a6 felbontásában. Ebből kapjuk, hogy ha 7|ak tetszőleges sorozatban, akkor 7|ak+2n, analg módon a másik 3 prímre is minden 3-ik illetve 6-ik szám osztható vele. Innét konstruálunk egy olyan x számot a kínai maradéktétellel, amire x 2(5), x 2(5), x 0(7.17) és x 0(7.17) és x 1(p), ahol p a6 prímosztója. Ugyanis ekkor minden 3k+1-.ik tag osztható 5-tel, 3k+2-ik 17-tel, 2k-ik 7-tel, és 6k+5-ik p-vel. De ezek lefedik az összes maradékosztályt, így ilyen számok jók, és tudunk olyant választani, hogy mindegyik prímnél nagyobb legyen. 1(p), ahol p a6 prímosztója. Ugyanis ekkor minden 3k+1-.ik tag osztható 5-tel, 3k+2-ik 17-tel, 2k-ik 7-tel, és 6k+5-ik p-vel. De ezek lefedik az összes maradékosztályt, így ilyen számok jók, és tudunk olyant választani, hogy mindegyik prímnél nagyobb legyen.
|
| Előzmény: [563] Radián, 2010-06-15 13:05:11 |
|
| [563] Radián | 2010-06-15 13:05:11 |
 Hello!
Ha valakinek megvan és van rá ideje kérem írja le a B.4272-es feladat megoldását. Előre is köszönöm.
|
|
| [562] BohnerGéza | 2010-06-03 16:10:11 |
 A B.4269 feladattal kapcsolatban fölvetek egy "sejtést" a GEOMETRIA témában, az 1422. hozzászólásban. Felhasználom az itteni 560. hozzászólás észrevételét, melynek bizonyítása is igen szép.
|
| Előzmény: [552] HoA, 2010-05-13 16:27:19 |
|
| [561] S.Ákos | 2010-05-16 00:24:35 |
 Ez független attól, hogy a körök sugarai egyenlők, tetszőleges AB szakaszon lévő belső pontra igaz, vagyis a beírt körök C-n át nem menő közös belső érintője átmegy az érintési ponton.
|
| Előzmény: [560] damil, 2010-05-15 21:22:28 |
|
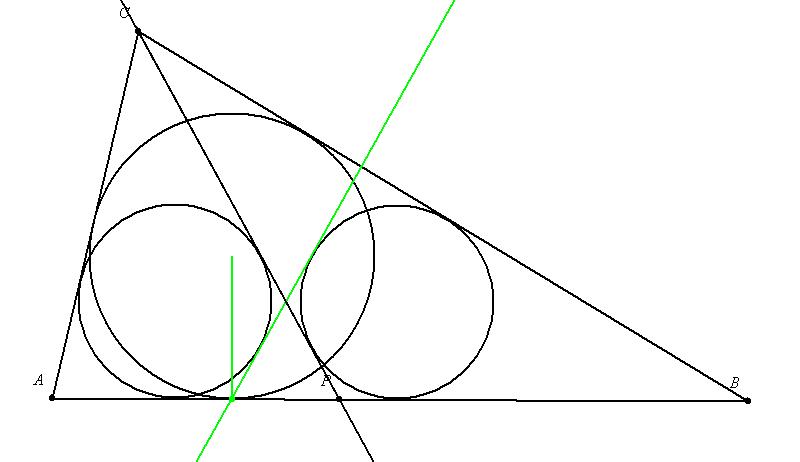
| [560] damil | 2010-05-15 21:22:28 |
 Itt egy ábra is amin kiemeltem a lényeget:
|
 |
|
| [559] damil | 2010-05-15 21:01:58 |
 Bocs, elfelejtettem odaírni, hogy közös belső érintő (külsőt se írtam, nem látom honnan szedted). Két közös belső érintő van (kivétel az egyenlő szárúaknál). Az egyikre illeszkedik C és P, és azt állítom hogy a másikra illeszkedik a a beírt kör és az AB oldal érintési pontja.
|
| Előzmény: [558] D. Tamás, 2010-05-15 11:29:15 |
|












 2(5), x
2(5), x
