| [659] Róbert Gida | 2011-08-09 00:27:07 |
 Nézzük meg tudja-e oldani a Mathematica az A jelű feladatot:
a = (b*c*d - b - c - d)/(1 - b*c - b*d - c*d);
Timing[FullSimplify[(a + b)*(c + d) + (a + d)*(b + c) >= 4*Sqrt[(1 + a*c)*(1 + b*d)], a > 0 && b > 0 && c > 0 && d > 0]]
{21.965 Second, True}
Húha, megdolgozott a Mathematica a válaszért. Kicsit segítettem is neki, ha az "a"-t nem fejezem ki, akkor nem bizonyítja be, visszaadja az eredetit. Az persze kérdéses, hogy minden esetben szabályos-e ez, azaz amivel leosztok az nem nulla, esetleg b-vel, c-vel, d-vel eljátszhatom ezt, ha "a"-val nem.
|
| Előzmény: [657] Tibixe, 2011-07-01 14:05:57 |
|
| [658] Janosov Milán | 2011-08-03 00:57:06 |
 Valaki tudja, az utolsó mérési feladat fura statisztikájának mi a magyarázata?
|
|
| [657] Tibixe | 2011-07-01 14:05:57 |
 Elég rögtön használni a számtani-mértani egyenlőtlenséget, homogenizálni és átrendezni.
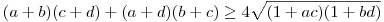
A számtani és mértani közép közti egyenlőtlenség miatt  . Ezért erősebb állítás, hogy . Ezért erősebb állítás, hogy
(a+b)(c+d)+(a+d)(b+c) 4+2ac+2bd 4+2ac+2bd
Kifejtve és kivonva:
ad+bc+ab+cd 4 4
A feltétellel szerint a+b+c+d=abc+abd+acd+bcd és itt mindkét oldal pozitív, tehát utóbbi két oldalával ekvivalens átalakításként szorozhatjuk az állítást:
(a+b+c+d)(ad+bc+ab+cd) 4(abc+abd+acd+bcd) 4(abc+abd+acd+bcd)
A zárójeleket felbontva és nullára rendezve:
a2b+a2d+ab2-2abc-2abd-2acd+ad2+b2c+bc2-2bcd+c2d+cd2 0 0
Ezt átírva:
(a+c)(b-d)2+(b+d)(a-c)2 0 0
Ez nyilván teljesül, mert nemnegatív teljes négyzetek nemnegatív együtthatós polinomja is nemnegatív.
|
| Előzmény: [655] sakkmath, 2011-07-01 08:44:32 |
|
|
| [655] sakkmath | 2011-07-01 08:44:32 |
 A KöMaL 2011/5-ös, májusi
számában megjelent
A.536. feladat egyik megoldása:
|
 |
|
| [654] Ali | 2011-06-03 07:53:07 |
 "Csak az a=b=1 esetet hagyod akkor ki."
Vszínűleg elkerülte a figyelmedet az utolsó mondat:
Ha pedig a=b 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1. 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1.
|
| Előzmény: [653] Róbert Gida, 2011-06-01 16:58:08 |
|
| [653] Róbert Gida | 2011-06-01 16:58:08 |
 "Legyenek először a és b relatív prímek (a,b)=1 és a>b (a>b feltehető, mivel a feladat a-ban és b-ben szimmetrikus)"
Csak az a=b=1 esetet hagyod akkor ki.
Szép megoldás. Amikor megláttam a feladatot nekem egyből a Válogatott feladatok és tételek az elemi matematika köréből (Aritmetika és algebra) 118. csillagos feladata ugrott be, nem tévedtem, a megoldás (és az egyenlet) hasonló: x2+y2+z2=kxyz. Ennek a feladatnak egy általánosítását már egyszer elsütötték A feladatként. Érdemes megvenni a könyvet.
|
| Előzmény: [652] Ali, 2011-06-01 16:00:37 |
|
| [652] Ali | 2011-06-01 16:00:37 |
 Megoldás A.533. -ra: Határozzuk meg mindazokat a pozitív egészekből álló (a,b,c) számhármasokat, amelyekre a2+b2 osztható (abc+1)-gyel.
Legyenek először a és b relatív prímek (a,b)=1 és a>b (a>b feltehető, mivel a feladat a-ban és b-ben szimmetrikus). Legyen továbbá k 1 olyan egész,melyre 1 olyan egész,melyre
Ha b>1 (b=1 eset később tisztázva bn=1-nél), akkor legyenek a1=b és b1=kbc-a. Ekkor fennál, hogy
Biz.: írjuk vissza a1 és b1 helyébe b-t és kbc-a-t: b2+(kbc-a)2=k(b(kbc-a)c+1). Rendezés után (1)-et kapjuk.
Fennáll továbbá, hogy 0<b1<b.
Biz.: k(a1b1c+1)=a12+b12 1 -ből következik, hogy a1b1c 1 -ből következik, hogy a1b1c 1/k-1>-1. Mivel a1 és c pozítív egészek és b1 egész, azért b1 1/k-1>-1. Mivel a1 és c pozítív egészek és b1 egész, azért b1 0. Felhasználva továbbá azt, hogy (a,b)=1 következik, hogy b1=(kbc-a)>0. Másrészt bb1<ab1=a(kbc-a)=b2-k<b2, tehát b1<b és nyilván b=a1<a. (a,b)=1-ből következik, hogy (b,kbc-a)=1, tehát (a1,b1)=1 is fennáll. 0. Felhasználva továbbá azt, hogy (a,b)=1 következik, hogy b1=(kbc-a)>0. Másrészt bb1<ab1=a(kbc-a)=b2-k<b2, tehát b1<b és nyilván b=a1<a. (a,b)=1-ből következik, hogy (b,kbc-a)=1, tehát (a1,b1)=1 is fennáll.
Azt kaptuk, hogy (a1,b1,c,k) -ra szintén teljesül (1).
Folytassuk a rekurziót egészen addig, míg b értéke 1 lesz. A rekurziós képlet:
| ai=bi-1,bi=kbi-1c-ai-1 | (3) |
A fenti gondolatmenetet megismételve kapjuk, hogy bi<bi-1=ai<ai-1 és (ai,bi)=1.
Legyen tehát an=bn-1,bn=kbn-1c-an-1=1. Ekkor an2+1=k(anc+1) és ezért anc+1|an2+1. Áll.: ez csak akkor lehetséges, ha an=c és k=1.
Biz.:Tegyük fel, hogy létezik c<an és l>1 úgy, hogy l(anc+1)=an2+1 an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc l l
következik,ami ellentmondás. Tehát an=c és k=1, továbbá an=bn-1>1 miatt c>1.
A (3) lineáris másodrendű rekurziót visszafelé megoldva a bn=1 és az an=c értékekből kiindulva c>2 esetén 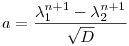 és és  , ahol , ahol  1,2 az x2-cx+1=0 egyenlet gyökei ( 1,2 az x2-cx+1=0 egyenlet gyökei ( 1> 1> 2), D az egyenlet diszkriminánsa és n 2), D az egyenlet diszkriminánsa és n 1. 1.
c=2 esetén a rekurzió az a=n+1 és b=n megoldást adja, ahol szintén n 1. 1.
Ezek pedig mind megoldások is. Ennek bizonyítása egyszerűen visszahelyettesítéssel történhet felhasználva, hogy  1+ 1+ 2=c, 2=c,  1. 1. 2=1 és D=c2-4, k=1. 2=1 és D=c2-4, k=1.
Nevezzük a továbbiakban az (a,b,c) hármast relatív prím megoldásnak, ha (a,b)=1. Legyen most (a,b,c) egy relatív prím megoldás, ahol c=d2c1, d>1, c1 1. Ilyen megoldás láttuk létezik. Ekkor (ad,bd,c1) egy nem relatív prím megoldás lesz, mivel (ad)(bd)c1+1=ab(d2c1)+1|a2+b2|(da)2+(db)2 1. Ilyen megoldás láttuk létezik. Ekkor (ad,bd,c1) egy nem relatív prím megoldás lesz, mivel (ad)(bd)c1+1=ab(d2c1)+1|a2+b2|(da)2+(db)2
Fordítva legyen (a,b,c) egy nem relatív prím megoldás (előbb láttuk ilyen létezik), melyben (a,b)=d>1, a=a1d, b=b1d, (a1,b1)=1. Ekkor mivel a1b1d2c+1|d2(a12+b12) és (a1b1d2c+1,d)=1, azért a1b1d2c+1|(a12+b12), tehát (a1,b1,d2c) egy relatív prím megoldás. Így minden nem relatív prím megoldás egyértelműen előáll egy relatív prím (a,b,c) megoldásból (ad,bd,c1) formában, ahol c=d2c1, d>1 és c1 1. 1.
Végül marad a c=1 eset. Láttuk, hogy relatív prím megoldás nem létezik c=1 esetén (ahhoz c>1 kellett). A nem relatív prím megoldások pedig azok az (ad,bd,1) alakú megoldások, melyekben (a,b,d2) egy relatív prím megoldás, ahol d>1.
Ha pedig a=b 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1. 1, akkor a2c+1|2a2 -ből triviálisan következik, hogy c=1 és a=1.
|
|
| [651] Róbert Gida | 2011-05-13 21:44:51 |
 Lejárt C1076. közölt megoldása érdekes.
Az ember azt hinné, hogy egy C feladatot azért nem lehet elszúrni, de mégis: "A gyökökre vonatkozó feltétel szerint a(a+1)-1=(a+1)2-a2" és itt van a hiba, a feladat a két gyök különbségéről beszélt, és még azt sem mondta, hogy a nagyobbikból a kisebbiket vonjuk ki. De, ha ezt feltesszük akkor is rossz, lásd a=-2, amikor (a+1)2-a2<0 teljesül.
Ki lehet számolni, nem jön be új megoldás, igazából ugyanezeket kapjuk meg még egyszer, de a közölt megoldás elvi hibás marad.
|
|
| [650] Róbert Gida | 2011-05-03 00:25:12 |
 Másik biz.: 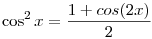 . De . De  , használjuk, hogy a csúcsok n, illetve n/2 csúcsú (minden csúcs 2-szer) szabályos sokszög csúcsaiba mennek át, attól függően, hogy n ptlan vagy ps, továbbá azt, hogy a szab. sokszög súlypontja az origó. Ebből már következik az állítás (n darab 1/2 lesz az összeg). Sinusra hasonló süthető el, vagy használjuk, hogy cos2x+sin2x=1 , használjuk, hogy a csúcsok n, illetve n/2 csúcsú (minden csúcs 2-szer) szabályos sokszög csúcsaiba mennek át, attól függően, hogy n ptlan vagy ps, továbbá azt, hogy a szab. sokszög súlypontja az origó. Ebből már következik az állítás (n darab 1/2 lesz az összeg). Sinusra hasonló süthető el, vagy használjuk, hogy cos2x+sin2x=1
|
| Előzmény: [648] bily71, 2011-05-02 21:43:27 |
|
|
| [648] bily71 | 2011-05-02 21:43:27 |
 Állítás:
Legyenek az origó középpontú, egységsugarú kör kerületére illeszkedő P1(x1,y1),P2(x2,y2),...,Pn(xn,yn) pontok egy szabályos n-szög csúcsai, ekkor 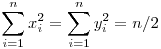 . .
Bizonyítás:
Legyen n=4m, húzzuk be az origón átmenő átlókat, ekkor van m darab egymásra merőleges átlópárunk (n,m N). N).
Tekintsük az AmA3m, A2mA4m átlópárt. Ha az Am pontba mutató vektor az x tengellyel  szöget zár be, akkor a koordináták így alakulnak Pm(cos szöget zár be, akkor a koordináták így alakulnak Pm(cos ,sin ,sin ),P2m(sin ),P2m(sin ,-cos ,-cos ),P3m(-cos ),P3m(-cos ,-sin ,-sin ),P4m(-sin ),P4m(-sin ,cos ,cos ) (0 ) (0    /2m). Ekkor xm2+x2m2+x3m2+x4m2=2(sin2 /2m). Ekkor xm2+x2m2+x3m2+x4m2=2(sin2 +cos2 +cos2 )=ym2+y2m2+y3m2+y4m2=2(sin2 )=ym2+y2m2+y3m2+y4m2=2(sin2 +cos2 +cos2 )=2. Ezt eljátszva a többi átlópárral kapjuk, hogy n=4m esetén )=2. Ezt eljátszva a többi átlópárral kapjuk, hogy n=4m esetén 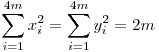 (0 (0    /2m). /2m).
n=2m esetén a problémát visszavezetjük az n=4m esetre: Töröljük a 4m-szög azon Pi csúcsait, ahol 2|i, ekkor kapunk egy szabályos 2m-szöget. Minden átlópár egyik tagja törölve lett a végpontokkal és azok koordinátáival együtt. Mivel xm2+x3m2=ym2+y3m2=x2m2+x4m2=y2m2+y4m2 és ez igaz minden átlópárra, azért 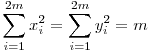 . .
n=m esetén a problémát visszavezetjük az n=2m esetre: Megintcsak töröljük a 2m-szög azon pi csúcsait, ahol 2|i, ekkor egy szabályos m szöget kapunk. Minden átló egyik végpontja törölve lett. Az átlók végpontjai az origóra tükrözve egymásba vihetők, ezért a koordinátáik egymás ellentettjei: Pi(xi,yi) Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy 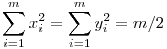 , m tetszőleges, tehát az állítás igaz bármely természetes számra. , m tetszőleges, tehát az állítás igaz bármely természetes számra.
|
| Előzmény: [647] jenei.attila, 2011-05-02 12:53:41 |
|
|
|
| [645] bily71 | 2011-04-29 13:17:39 |
 A feladat szerint az Ai pontok egy kör kerületén helyezkednek el, hát legyen ez a kör az egységsugarú, origó középpontú kör.
A feladat szerint az A1A3 szakasz az A2 pontból  /2n szögben látszik, vagyis az A1,A3 pontok által határolt körív kerületi szöge /2n szögben látszik, vagyis az A1,A3 pontok által határolt körív kerületi szöge  /2n (a pontok egy kör kerületén vannak!), vagyis a körív középponti szöge /2n (a pontok egy kör kerületén vannak!), vagyis a körív középponti szöge  /n. /n.
Az A3A5 szakasz az A4 pontból ugyancsak  /2n szögben látszik, vagyis a szakasz az origóból ugyancsak /2n szögben látszik, vagyis a szakasz az origóból ugyancsak  /n szögben látszik, ez csak úgy lehetséges, ha az A1,A3,A5 pontok egy a körbeírt szabályos 2n-szög csúcsai. Ugyanezt eljátszva az öszes Ai ponttal, ahol i páratlan, kapjuk, hogy az Ai pontok egy szabályos 2n-szög csúcsai. (Persze, az Ai pontok halmaza csak részhalmaza a 2n-szög csúcsai halmazának.) /n szögben látszik, ez csak úgy lehetséges, ha az A1,A3,A5 pontok egy a körbeírt szabályos 2n-szög csúcsai. Ugyanezt eljátszva az öszes Ai ponttal, ahol i páratlan, kapjuk, hogy az Ai pontok egy szabályos 2n-szög csúcsai. (Persze, az Ai pontok halmaza csak részhalmaza a 2n-szög csúcsai halmazának.)
Az is nyílvánvaló, hogy az A1A2n+1 szakasz átmegy az origón. Forgassuk az A1 pontot a (0,1), az A2n+1-et a (0,-1) pontba.
Ugyanígy az Aj pontok is, ahol j páros, egy szabályos 2n szög csúcsai. Az A1A2 szakasz az origóból a feladat szerint tetszőleges  szögben látszik, ahol a feltételek miatt 0 szögben látszik, ahol a feltételek miatt 0    /n, vagyis ezt a 2n-szöget origókörüli, /n, vagyis ezt a 2n-szöget origókörüli,  -szögű forgatással kapjuk az előzőből. -szögű forgatással kapjuk az előzőből.
A feladat szerint az l1 szakasz egyik végpontja az A1 pont (én most azonosítottam a szakasz hosszát magával a szakasszal, ha nem baj), a másikat jelöljük M1-gyel, amely pont egyben az l2 szakasz egyik végpontja, a másikat jelöljük M2-vel, ezt folytatva kapjuk az M1,M2,...,M2n-2 pontokat.
Az A1A2M1, A2M1M2, A3M2M3,...,A2nM2n-2A2n+1 háromszögek hasonlók, hiszen a feladat szerint az A2,A3,...,A2n-1,A2n csúcsokban elhelyezkedő szögek mindegyike  /2n. Ezek egyben váltószögek, hiszen a megfelelő száraik közösek, továbbá az összes háromszög egyik oldala egy egyenesre, az y tengelyre illeszkedik, a így a háromszögek oldalai páronkét párhuzamosak, vagyis hasonlóak. /2n. Ezek egyben váltószögek, hiszen a megfelelő száraik közösek, továbbá az összes háromszög egyik oldala egy egyenesre, az y tengelyre illeszkedik, a így a háromszögek oldalai páronkét párhuzamosak, vagyis hasonlóak.
Mivel a háromszögek hasonlóak, bennük a megfelelő oldalak és a hozzájuk tartozó magasságok aránya állandó, jelöljük ezt c-vel, c 0. 0.
A feladat szerint l12-l22+l32-l42+...-l2n-22+l2n-12=0, vagyis 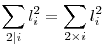 , ahol 1 , ahol 1 i i 2n-1 és ×: "nem osztója". 2n-1 és ×: "nem osztója".
Ha az előző teljesül az li szakaszokra, akkor teljesül a rájuk emelt magasságra is, azaz  (minden li szakasz az előbb részletezett háromszögek közül az egyik alapja), ugyanis mi=lic-t behelyettesítve (minden li szakasz az előbb részletezett háromszögek közül az egyik alapja), ugyanis mi=lic-t behelyettesítve 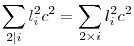 , ebből , ebből 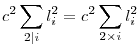 . Mivel c . Mivel c 0, ezért leoszthatunk c2-tel, így visszakapjuk az eredeti állítást, tehát elég az mi-kre belátni. 0, ezért leoszthatunk c2-tel, így visszakapjuk az eredeti állítást, tehát elég az mi-kre belátni.
Vegyük észre, hogy az mi szakasz hossza megegyezik az Ai+1 pontba (ami az mi-hez tartozó háromszög csúcsa) mutató helyvektor x koordinátájának "hosszával", ugyanis az mi-k, mivel magasságok, merőlegesek az alapokra, melyek az y tengelyere illeszkednek, így merőlegesek az y tengelyre, így a vetületük hossza egyenlő az Ai+1 pont vetülete és az origó közti távolsággal, ami definíció szerint épp a pont x koordinátájnak abszolút értéke.
Szerintem még mindig pontatlan, de ha visszamegyünk az axiómákig, akkor sosem érünk a végére.
Folyt. köv.
|
| Előzmény: [641] Maga Péter, 2011-04-29 10:09:22 |
|
|
|
| [642] bily71 | 2011-04-29 10:52:31 |
 "...ez a megoldás hibás, legalábbis erősen hiányos."
Nem hibás, de valóban erősen hiányos, legalábbis az, amit leírtam. Készíts ábrát és azonnal megérted a gondolatmenetem. Ha mégsem, leírom precízebben.
|
| Előzmény: [641] Maga Péter, 2011-04-29 10:09:22 |
|
| [641] Maga Péter | 2011-04-29 10:09:22 |
 Nem oldottam meg a feladatot, nem is nagyon gondolkodtam rajta, úgyhogy a partvonalon túlról szólok (és könnyen lehet, hogy tévedek): ez a megoldás hibás, legalábbis erősen hiányos. Az első két bekezdés már első ránézésre is elképesztő pontatlanságokat tartalmaz. De utána is 'valami bűzlik Dániában', ahogy mondani szokás.
|
| Előzmény: [640] bily71, 2011-04-28 19:15:23 |
|
| [640] bily71 | 2011-04-28 19:15:23 |
 A.530.
Legyen a kör az origó középpontú egységkör, továbbá legyen A1(0,1) és A2n+1(0,-1)!
A kerületi és középponti szögek tételéből következik, hogy az A1, A3,...,A2n+1 pontok egy szabályos 2n-szög csúcsai. Az A2, A4,...,A2n pontok ugyancsak egy szabályos 2n-szög csúcsai, melyet az előbbi 2n-szögből origó körüli  szögű forgatással kapunk (0 szögű forgatással kapunk (0    /n). /n).
Jelöljük az A1A2n+1 és az A2A3, A3A4,...,A2nA2n+1 szakaszok metszéspontjait M1, M2,...,M2n-nel! Ekkor az A1A2M1, A3M1M2,...,A2nM2n-2A2n+1 háromszögek hasonlóak, ugyanis az A1A2M1 , M1A3M2 , M1A3M2 ,...,M2n-2,A2nA2n+1 ,...,M2n-2,A2nA2n+1 szögek váltószögek és a háromszögek alapjai egy egynesre (az y tengelyre) esnek, így az oldalaik páronként párhuzamosak. szögek váltószögek és a háromszögek alapjai egy egynesre (az y tengelyre) esnek, így az oldalaik páronként párhuzamosak.
Mivel a hárömszögek hasonlóak, az alap és a ráemelt magasság aránya mindegyikben megegyezik, vagyis mi/ i=c i=c  mi= mi= ic ic  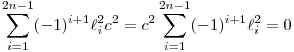 , c , c 0 0   . Tehát elég azt megmutatni, hogy . Tehát elég azt megmutatni, hogy 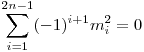 teljesül. teljesül.
Vegyük észre, hogy a magasság hossza a háromszög alapjával szemközti csúcsába mutató helyvektor x koordinátájának abszolút értékével egyezik meg.
Legyenek egy szabályos n-szög csúcsainak koordinátái x1,y1, x2,y2, ...,xn,yn, ekkor 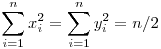 . (A bizonyítást, ha szükséges, leírom.) . (A bizonyítást, ha szükséges, leírom.)
Ha az A3, A5,...,A2n+1 pontokat tükrözzük az origóra, akkor egy szabályos 2n-szöget kapunk. Mivel az Ai és az Ai' pontok x koordinátáinak abszolút értéke megyegyezik, ezért  . Ugyanígy eljárva az A2, A4,...,A2n pontokkal kapjuk, hogy . Ugyanígy eljárva az A2, A4,...,A2n pontokkal kapjuk, hogy 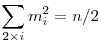 , (×: nem osztható) ebből , (×: nem osztható) ebből   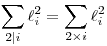   , vagyis az állítás igaz. , vagyis az állítás igaz.
|
|
|
| [638] jonas | 2011-04-24 13:18:05 |
 Ez gyors volt. Nekem majdnem egy évbe telt, amíg megtaláltam a Lovászban, pedig hamarabb kellett volna. Most már egyébként három lényegesen különböző megoldást is tudok a feladatra. Ha gondolod, szorgalmi feladatként találd meg mind a hármat.
Azzal vitatkoznék, hogy hipergráfokkal egyszerűbb a megfogalmazás. Szerintem nem, de más is mondta már, hogy igen.
|
| Előzmény: [636] Róbert Gida, 2011-04-23 21:58:42 |
|
|
| [636] Róbert Gida | 2011-04-23 21:58:42 |
 Így már érthető. Ha már észrevettem a hipergráfos átfogalmazást, gondoltam megnézem Lovász Kombinatorikai problémák és feladatok c. könyvében, hogy megtalálom-e. 13. fejezet 27. példája pontosan ez, kínairól matematika nyelvére lefordítva (13. fejezet a hipergráfos.) És csak fél métert kellett nyúlnom érte az asztalomon.
janomo, ezt is veheted egy általam elmondott nehéz feladatnak.
|
| Előzmény: [635] Kemény Legény, 2011-04-23 19:10:47 |
|
| [635] Kemény Legény | 2011-04-23 19:10:47 |
 Szerintem félreolvashattál valamit, talán azt, hogy "...amelyre C bármely két elemének és A-nak van közös eleme". Amit te feltételezel, az az, hogy C bármely három elemének kell legyen közös eleme, amit semmi sem garantál.
|
| Előzmény: [634] Róbert Gida, 2011-04-23 18:01:45 |
|





 4+2ac+2bd
4+2ac+2bd


 an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc
an(an-lc)=l-1>0. Ezért egyrészt an|l-1 és így an<l, másrészt an-lc>0, ebből pegig an>lc 1,2 az x2-cx+1=0 egyenlet gyökei (
1,2 az x2-cx+1=0 egyenlet gyökei (


 /2m kikötés felesleges,
/2m kikötés felesleges,  N).
N).  Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy
Pi'(-xi,-yi), vagyis xi2=(-xi)2, yi2=(-yi)2. Ebből már következik, hogy  0.
0. 
 , M1A3M2
, M1A3M2 i=c
i=c 