Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[679] Róbert Gida

2011-08-18 23:59:02

B.4355. Egy nagyon munkás bizonyítás: helyettesítsünk be 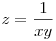$z=\frac {1}{xy}$ -t, rendezzük az egyenlőtlenséget nullára. Ekkor egy olyan törtet kapunk, aminek a nevezője pozitív (csak pozitív tagok szorzatából áll), így az kell, hogy a számláló pozitív minden x,y>0 esetén, ami végülis azt jelenti, hogy: (ezt a Mathematica is egyből megadja nekünk):

1+x²y+xy²+2x⁴y²+2x³y³+x⁶y³+2x²y⁴+2x⁵y⁴+x⁸y⁴+2x⁴y⁵+x⁷y⁵+2x¹⁰y⁵+x³y⁶

+2x⁶y⁶+2x⁹y⁶+x¹²y⁶+x⁵y⁷+2x⁸y⁷+2x¹¹y⁷+x¹⁴y⁷+x⁴y⁸+2x⁷y⁸+2x¹⁰y⁸+x¹³y⁸+2x⁶y⁹+x⁹y⁹

+2x¹²y⁹+2x⁵y¹⁰+2x⁸y¹⁰+x¹¹y¹⁰+2x⁷y¹¹+x¹⁰y¹¹+x⁶y¹²+2x⁹y¹²+x⁸y¹³+x⁷y¹⁴ $\ge$ 2x⁵y³+2x⁴y⁴+2x⁷y⁴

+2x³y⁵+4x⁶y⁵+2x⁹y⁵+4x⁵y⁶+4x⁸y⁶+2x⁴y⁷+6x⁷y⁷+2x¹⁰y⁷+4x⁶y⁸+4x⁹y⁸+2x⁵y⁹+4x⁸y⁹+2x¹¹y⁹

+2x⁷y¹⁰+2x¹⁰y¹⁰+2x⁹y¹¹

(Rendezéssel, hogy mindkét oldalon pozitív tagok álljanak). A bal, illetve a jobb oldalon álló tagok súlyozott mértani közepe egyaránt (xy)⁷. Így reménykedhetünk abban, hogy kizárólag számtani mértani egyenlőtlenségekkel be tudjuk bizonyítani az állítást, és ez valóban így van: 54 darab számtani-mértani egyenlőtlenséget felírva és összeadva kapjuk a bizonyítandó állítást:

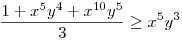
$\frac{1+x^{5}y^{4}+x^{10}y^{5}}{3}\ge x^{5}y^{3}$

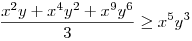
$\frac{x^{2}y+x^{4}y^{2}+x^{9}y^{6}}{3}\ge x^{5}y^{3}$

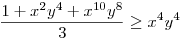
$\frac{1+x^{2}y^{4}+x^{10}y^{8}}{3}\ge x^{4}y^{4}$

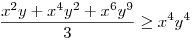
$\frac{x^{2}y+x^{4}y^{2}+x^{6}y^{9}}{3}\ge x^{4}y^{4}$

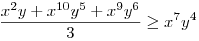
$\frac{x^{2}y+x^{10}y^{5}+x^{9}y^{6}}{3}\ge x^{7}y^{4}$

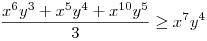
$\frac{x^{6}y^{3}+x^{5}y^{4}+x^{10}y^{5}}{3}\ge x^{7}y^{4}$

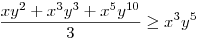
$\frac{xy^{2}+x^{3}y^{3}+x^{5}y^{10}}{3}\ge x^{3}y^{5}$

$\frac{x^{3}y^{3}+x^{2}y^{4}+x^{4}y^{8}}{3}\ge x^{3}y^{5}$

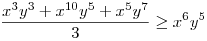
$\frac{x^{3}y^{3}+x^{10}y^{5}+x^{5}y^{7}}{3}\ge x^{6}y^{5}$

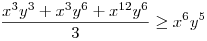
$\frac{x^{3}y^{3}+x^{3}y^{6}+x^{12}y^{6}}{3}\ge x^{6}y^{5}$

$\frac{x^{2}y^{4}+x^{5}y^{4}+x^{11}y^{7}}{3}\ge x^{6}y^{5}$

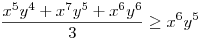
$\frac{x^{5}y^{4}+x^{7}y^{5}+x^{6}y^{6}}{3}\ge x^{6}y^{5}$

$\frac{x^{4}y^{2}+x^{9}y^{6}+x^{14}y^{7}}{3}\ge x^{9}y^{5}$

$\frac{x^{8}y^{4}+x^{10}y^{5}+x^{9}y^{6}}{3}\ge x^{9}y^{5}$

$\frac{xy^{2}+x^{5}y^{4}+x^{9}y^{12}}{3}\ge x^{5}y^{6}$

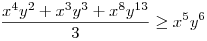
$\frac{x^{4}y^{2}+x^{3}y^{3}+x^{8}y^{13}}{3}\ge x^{5}y^{6}$

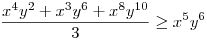
$\frac{x^{4}y^{2}+x^{3}y^{6}+x^{8}y^{10}}{3}\ge x^{5}y^{6}$

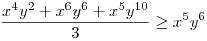
$\frac{x^{4}y^{2}+x^{6}y^{6}+x^{5}y^{10}}{3}\ge x^{5}y^{6}$

$\frac{x^{6}y^{3}+x^{8}y^{7}+x^{10}y^{8}}{3}\ge x^{8}y^{6}$

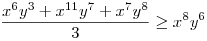
$\frac{x^{6}y^{3}+x^{11}y^{7}+x^{7}y^{8}}{3}\ge x^{8}y^{6}$

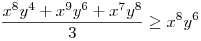
$\frac{x^{8}y^{4}+x^{9}y^{6}+x^{7}y^{8}}{3}\ge x^{8}y^{6}$

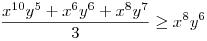
$\frac{x^{10}y^{5}+x^{6}y^{6}+x^{8}y^{7}}{3}\ge x^{8}y^{6}$

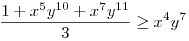
$\frac{1+x^{5}y^{10}+x^{7}y^{11}}{3}\ge x^{4}y^{7}$

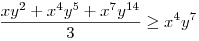
$\frac{xy^{2}+x^{4}y^{5}+x^{7}y^{14}}{3}\ge x^{4}y^{7}$

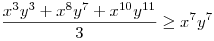
$\frac{x^{3}y^{3}+x^{8}y^{7}+x^{10}y^{11}}{3}\ge x^{7}y^{7}$

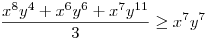
$\frac{x^{8}y^{4}+x^{6}y^{6}+x^{7}y^{11}}{3}\ge x^{7}y^{7}$

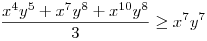
$\frac{x^{4}y^{5}+x^{7}y^{8}+x^{10}y^{8}}{3}\ge x^{7}y^{7}$

$\frac{x^{7}y^{5}+x^{6}y^{6}+x^{8}y^{10}}{3}\ge x^{7}y^{7}$

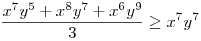
$\frac{x^{7}y^{5}+x^{8}y^{7}+x^{6}y^{9}}{3}\ge x^{7}y^{7}$

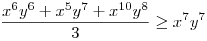
$\frac{x^{6}y^{6}+x^{5}y^{7}+x^{10}y^{8}}{3}\ge x^{7}y^{7}$

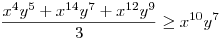
$\frac{x^{4}y^{5}+x^{14}y^{7}+x^{12}y^{9}}{3}\ge x^{10}y^{7}$

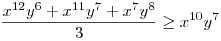
$\frac{x^{12}y^{6}+x^{11}y^{7}+x^{7}y^{8}}{3}\ge x^{10}y^{7}$

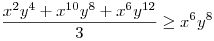
$\frac{x^{2}y^{4}+x^{10}y^{8}+x^{6}y^{12}}{3}\ge x^{6}y^{8}$

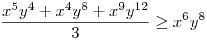
$\frac{x^{5}y^{4}+x^{4}y^{8}+x^{9}y^{12}}{3}\ge x^{6}y^{8}$

$\frac{x^{3}y^{6}+x^{6}y^{9}+x^{9}y^{9}}{3}\ge x^{6}y^{8}$

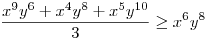
$\frac{x^{9}y^{6}+x^{4}y^{8}+x^{5}y^{10}}{3}\ge x^{6}y^{8}$

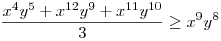
$\frac{x^{4}y^{5}+x^{12}y^{9}+x^{11}y^{10}}{3}\ge x^{9}y^{8}$

$\frac{x^{5}y^{7}+x^{14}y^{7}+x^{8}y^{10}}{3}\ge x^{9}y^{8}$

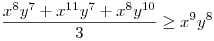
$\frac{x^{8}y^{7}+x^{11}y^{7}+x^{8}y^{10}}{3}\ge x^{9}y^{8}$

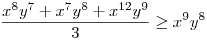
$\frac{x^{8}y^{7}+x^{7}y^{8}+x^{12}y^{9}}{3}\ge x^{9}y^{8}$

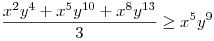
$\frac{x^{2}y^{4}+x^{5}y^{10}+x^{8}y^{13}}{3}\ge x^{5}y^{9}$

$\frac{x^{2}y^{4}+x^{7}y^{11}+x^{6}y^{12}}{3}\ge x^{5}y^{9}$

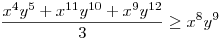
$\frac{x^{4}y^{5}+x^{11}y^{10}+x^{9}y^{12}}{3}\ge x^{8}y^{9}$

$\frac{x^{11}y^{7}+x^{6}y^{9}+x^{7}y^{11}}{3}\ge x^{8}y^{9}$

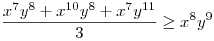
$\frac{x^{7}y^{8}+x^{10}y^{8}+x^{7}y^{11}}{3}\ge x^{8}y^{9}$

$\frac{x^{13}y^{8}+x^{6}y^{9}+x^{5}y^{10}}{3}\ge x^{8}y^{9}$

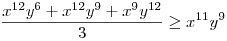
$\frac{x^{12}y^{6}+x^{12}y^{9}+x^{9}y^{12}}{3}\ge x^{11}y^{9}$

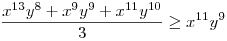
$\frac{x^{13}y^{8}+x^{9}y^{9}+x^{11}y^{10}}{3}\ge x^{11}y^{9}$

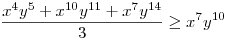
$\frac{x^{4}y^{5}+x^{10}y^{11}+x^{7}y^{14}}{3}\ge x^{7}y^{10}$

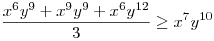
$\frac{x^{6}y^{9}+x^{9}y^{9}+x^{6}y^{12}}{3}\ge x^{7}y^{10}$

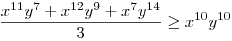
$\frac{x^{11}y^{7}+x^{12}y^{9}+x^{7}y^{14}}{3}\ge x^{10}y^{10}$

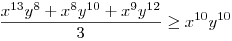
$\frac{x^{13}y^{8}+x^{8}y^{10}+x^{9}y^{12}}{3}\ge x^{10}y^{10}$

$\frac{x^{12}y^{9}+x^{7}y^{11}+x^{8}y^{13}}{3}\ge x^{9}y^{11}$

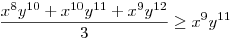
$\frac{x^{8}y^{10}+x^{10}y^{11}+x^{9}y^{12}}{3}\ge x^{9}y^{11}$

Előzmény: [673] Blinki Bill, 2011-08-17 18:05:18

[678] Fálesz Mihály	2011-08-18 14:57:15
Leírok egy lehetséges megoldást. (Nem saját; Ilja Bogdanovtól hallottam.) A. 505. Az ABCD húrnégyszögben O₁ és O₂ az ABC, illetve az ABD háromszögbe írt kör középpontja. Az O₁O₂ egyenes a BC egyenest E-ben, az AD egyenest F-ben metszi. (a) Igazoljuk, hogy létezik egy olyan k kör, ami E-ben, illetve F-ben érinti a BC és az AD egyenest. (b) Mutassuk meg, hogy k érinti az ABCD négyszög köré írt kört is. 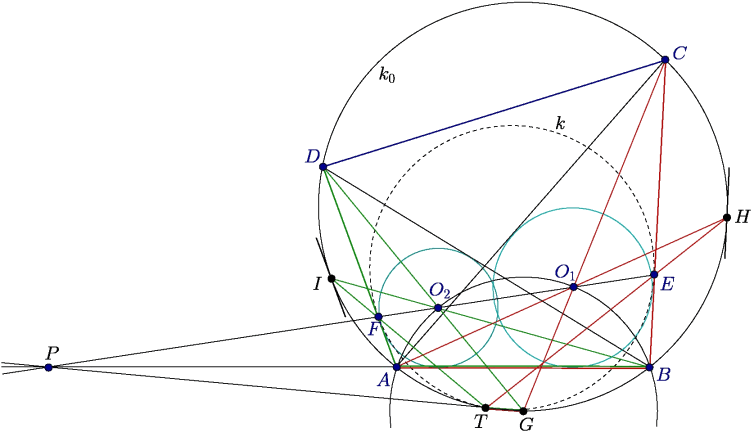Javasolta: Nagy János (Budapest) Megoldás. (a) Jelöljük a körülírt kört k₀-nal, és legyen G,H,I rendre a kör AB, BC, DA íveinek felezőpontja. Az ABC háromszögben AH és CG szögfelezők, tehát O₁ ezek metszéspontja; hasonlóan O₂ a BI és DG húrok metszéspontja. Ismert továbbá, hogy O₁ és O₂ rajta van a G középpontú, A-n és B-n átmenő körön. Az O₁O₂G háromszög tehát egyenlő szárú. 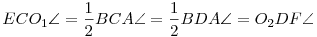A CO₁E és DO₂F háromszögekben $ECO_1\angle = \frac12 BCA\angle = \frac12 BDA\angle = O_2DF \angle$ és CO₁E $\angle$ =GO₁O₂ $\angle$ =O₁O₂G $\angle$ =FO₂D $\angle$ , tehát FEC $\angle$ =DFE $\angle$ . Ebből pedig következik, hogy létezik a BC egyenest E-ben, az AD egyenest F-ben érintő k kör. (b) Legyen az AB és EF egyenesek metszéspontja P, a PG egyenes és k₀ második metszéspontja T. (Ha AB és EF párhuzamosak, akkor P a két egyenes ideális pontja és T=G.) A Pascal-tételt az ABCGTH (piros) hatszögre alkalmazva kapjuk, hogy AB $\cap$ GT=P, CG $\cap$ HA=O₁ és BC $\cap$ TH egy egyenesen van; következésképp a TH egyenes átmegy az E ponton. Hasonlóan, a Pascal-tételt a BADGTI (zöld) hatszögre alkalmazva kapjuk, hogy a TI egyenes átmegy az F ponton. A k₀ körhöz H-ban és I-ben, illetve a k-hoz E-ben és F-ben húzott érintők párhuzamosak. Ezért a HE egyenes és az IF egyenes is átmegy a két kör külső hasonlósági pontján. Tehát HE $\cap$ IF=T a két kör külső hasonlósági pontja. De a hasonlósági pont csak akkor lehet rajta valamelyik körön, ha a két kör érinti egymást.

Előzmény: [672] HoA, 2011-08-17 11:50:13

[677] Fálesz Mihály

2011-08-18 11:46:45

A számlálók barátságosan magas fokúak, és ez sokféle más megoldást lehetővé tesz. Például céltudatosan becsülhetjük a számlálókat az

$a^3+b^3 \ge \frac23 \sqrt{ab}\big(a^2+ab+b^2\big)$

(*)

egyenlőtlenséggel, hogy utána felírhassuk a számtani és mértani közepek közötti egyenlőtlenséget a három tagra:

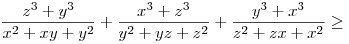
$\frac{z^3 + y^3}{x^2+xy+y^2} + \frac{x^3 + z^3}{y^2+yz+z^2} + \frac{y^3 + x^3}{z^2+zx+x^2} \ge$

$\ge \frac{\frac23 \sqrt{zy}\big(z^2+zy+y^2\big)}{x^2+xy+y^2}+ \frac{\frac23 \sqrt{xz}\big(x^2+xz+z^2\big)}{y^2+yz+z^2}+ \frac{\frac23 \sqrt{yx}\big(y^2+yx+x^2\big)}{z^2+zx+x^2} \ge$

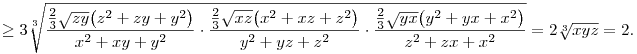
$\ge 3\root3\of{ \frac{\frac23 \sqrt{zy}\big(z^2+zy+y^2\big)}{x^2+xy+y^2}\cdot \frac{\frac23 \sqrt{xz}\big(x^2+xz+z^2\big)}{y^2+yz+z^2}\cdot \frac{\frac23 \sqrt{yx}\big(y^2+yx+x^2\big)}{z^2+zx+x^2}} = 2\root3\of{xyz} = 2.$

(*) egy lehetséges bizonyítása:

$3(a^3+b^3) - 2\sqrt{ab}\big(a^2+ab+b^2\big) = \big(\sqrt{a}-\sqrt{b}\big)^2\big( 3a^2+4a^{3/2}b^{1/2}+5ab+4a^{1/2}b^{3/2}+3b^2\big)\ge0.$

Előzmény: [676] Maga Péter, 2011-08-18 08:41:47

[676] Maga Péter	2011-08-18 08:41:47
Igazad van, ezt elnéztem. De akkor már (legalábbis nekem) egyszerűbbnek tűnik az a kiegészítés, hogy az x $\geq$ y $\geq$ z esetben az első két soromban minden egyenlőtlenség megfordul, és a rendezési tétel arra írható fel ugyanazzal az eredménnyel.
Előzmény: [675] Kemény Legény, 2011-08-18 07:31:19

[675] Kemény Legény

2011-08-18 07:31:19

"Nyilván feltehető a x $\leq$ y $\leq$ z rendezés."

Ez igaz, de szerintem nem annyira nyilvánvaló. Az eredeti képletben csak a ciklikus szimmetria látszik ránézésre, ami alapján csak az tehető fel, hogy x $\leq$ y $\leq$ z vagy x $\geq$ y $\geq$ z. A teljes szimmetria nekem csak az alábbi egyenlőség miatt nyilvánvaló:

$\frac{z^3 + y^3}{x^2+xy+y^2} + \frac{x^3 + z^3}{y^2+yz+z^2} + \frac{y^3 + x^3}{z^2+zx+x^2} = \frac{z^3 + x^3}{x^2+xy+y^2} + \frac{x^3 + y^3}{y^2+yz+z^2} + \frac{y^3 + z^3}{z^2+zx+x^2}$

Értem én, hogy ez csak egy ötlet/vázlat volt a megoldáshoz, de ez a rész talán említésre méltó lehet.

Előzmény: [674] Maga Péter, 2011-08-17 20:15:45

[674] Maga Péter

2011-08-17 20:15:45

Nyilván feltehető a x $\leq$ y $\leq$ z rendezés. Ekkor egyrészt

x³+y³ $\leq$ x³+z³ $\leq$ y³+z³,

másrészt

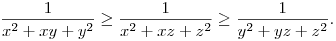
$\frac{1}{x^2+xy+y^2}\geq \frac{1}{x^2+xz+z^2}\geq \frac{1}{y^2+yz+z^2}.$

Ekkor a bizonyítandó egyenlőtlenség bal oldala a rendezési tétel értelmében alulról becsülhető azzal, hogy

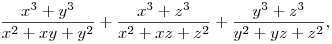
$\frac{x^3+y^3}{x^2+xy+y^2}+\frac{x^3+z^3}{x^2+xz+z^2}+\frac{y^3+z^3}{y^2+yz+z^2},$

elég tehát erről megmutatni, hogy ez $\geq$ 2. Ennek egy tipikus tagja

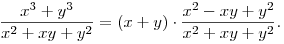
$\frac{x^3+y^3}{x^2+xy+y^2}=(x+y)\cdot\frac{x^2-xy+y^2}{x^2+xy+y^2}.$

Innen már menni fog:), ha mégsem, szólj!

Előzmény: [673] Blinki Bill, 2011-08-17 18:05:18

[673] Blinki Bill	2011-08-17 18:05:18
Sziasztok, kérhetnék egy kis ötletet (indítót) a B.4355-höz (április)?Köszönöm.

[672] HoA	2011-08-17 11:50:13
Fel tudná tenni valaki az A 505. ( 2010. március ) lapban közölt megoldásának vázlatát? Itt csak egy statisztikát érek el és szeretnék a feladathoz hozzátenni valamit, de nem szeretnék ismétlésbe esni. Köszönöm.

[671] Szabó Attila	2011-08-15 22:18:12
Nem tudja valaki, hogy miért nem kapott senki pontot a májusi mérési feladatra és miért nem javították ki a beküldött dolgozatokat?

[670] sakkmath	2011-08-12 23:36:47
Igazad van, köszönöm. A vázlatom tehát alapos átdolgozásra szorul.
Előzmény: [666] Lóczi Lajos, 2011-08-12 14:29:44

[669] Róbert Gida	2011-08-12 18:21:55
Akarom mondani: S(2ⁿ) végtelenbe tart, ha n tart végtelen volt a példa, ha jól emlékszem.
Előzmény: [668] Róbert Gida, 2011-08-12 18:01:19

[668] Róbert Gida

2011-08-12 18:01:19

Voltak már hasonló példák, leginkább az S(2ⁿ) nem korlátos ősrégi N jelű feladatra gondolok.

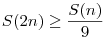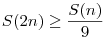B4360: Belátom először, hogy k=2 jó. Részben indukcióval csinálom. Állításom: $S(2n)\ge \frac {S(n)}{9}$ . Ez n<10-re teljesül. Ha n $\ge$ 10 és n-nek van 5-nél kisebb számjegye, akkor ott elvágjuk n-et és indukcióval teljesül az állítás n-re is. Így feltehető, hogy n minden jegye legalább 5, akkor minden helyiértéken van átvitel a szorzásnál, így a következő jegy a szorzatban nem lehet nulla, hiszen (2*d+1)mod 10 a jegy, ami páratlan, így nem nulla. Azaz L jegyű n esetén S(n) $\le$ 9L (ez trivi), míg S(2n) $\ge$ L, hiszen a rákövetkező jegy mindig legalább 1. Kettőből: $S(2n)\ge \frac {S(n)}{9}$ , ami kellett. Teljesen hasonló a biz. k=5-re is. 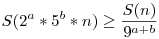Indukcióval ebből: $S(2^a*5^b*n)\ge \frac {S(n)}{9^{a+b}}$ , így, ha k=2^a*5^b, akkor az megoldás lesz.

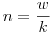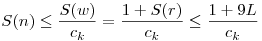Más megoldás nincs: legyen k az L jegyű, így k<10^L. Legyen N $\ge$ L tetszőleges, és w az az egyértelmű k-val osztható egész, amelyre w=10^N+r, ahol 0 $\le$ r<k teljesül. Ekkor r=0 nem lehet, különben k|10^N, de k akkor 2^a*5^b alakú szám lenne, ellentmondás. w osztható k-val, így legyen $n=\frac wk$ . Indirekt feltevés miatt S(kn) $\ge$ c_kS(n), innen: $S(n)\le \frac {S(w)}{c_k}=\frac {1+S(r)}{c_k}\le \frac {1+9L}{c_k}$ , azaz S(n) korlátos. (L és c_k is konstans). És ez nem lehet.

Legyen n 10-es számrendszeres ábrázolása:

$n=\sum_{i=0}^{s-1}d_i*10^{a_i}$

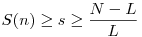, ahol d_i>0 és az a₀<a₁<...<a_s-1. Ekkor a₀ $\le$ L, minden i-re, a_i-a_i-1 $\le$ L, a_s-1 $\ge$ N-L, ezekből már kövekezni fog az ellentmondás, mert ekkor indukcióval: a_i $\le$ (i+1)L, de a_s-1 $\ge$ N-L, így $S(n)\ge s\ge \frac {N-L}{L}$ , azaz S(n) nem korlátos, ellentmondás.

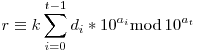Ha a₀>L, akkor n osztható 10^L-el, de akkor w=kn is, ellentmondás, mert N $\ge$ L, így w az 10^L-el osztva r maradékot ad, de r nem nulla. w>10^N és k<10^L, így $n=\frac wk>10^{N-L}$ , ezért a_s-1 $\ge$ N-L. Végül minden i-re a_i $\le$ a_i-1+L, indirekte legyen: a_t>a_t-1+L esetén tekintsük az $10^N+r=w=kn=k\sum_{i=0}^{s-1}d_i*10^{a_i}$ , tekintsük ezt modulo 10^a_t, ekkor $r\equiv k\sum_{i=0}^{t-1}d_i*10^{a_i} \mod {10^{a_t}}$ , ez modulo nélkül is teljesül egyenlőséggel, mert k<10^L és a_t-1+L<a_t. 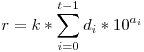Azaz $r=k*\sum_{i=0}^{t-1}d_i*10^{a_i}$ , jobb oldal osztható k-val, de a bal oldal nem, ellentmondás.

Előzmény: [663] Róbert Gida, 2011-08-12 01:09:50

[667] SmallPotato	2011-08-12 17:33:01
Szép, igényes, és (számomra legalábbis) igen tanulságos munka!
Előzmény: [666] Lóczi Lajos, 2011-08-12 14:29:44

[666] Lóczi Lajos

2011-08-12 14:29:44

Csak óvatosan! A 2.) lépésbeli 2. állításod általában nem igaz! Egy függvény grafikonja és inverze grafikonjának metszéspontja "bárhol" lehet!

Ezzel kapcsolatban lásd a megfelelő KöMaL-cikket, amely pl. elérhető itt:

www.berzsenyi.hu/erben/rlv/2010/abraham_gabor.ppt

Előzmény: [665] sakkmath, 2011-08-12 14:09:05

[665] sakkmath

2011-08-12 14:09:05

Vázlat B.4358.-hoz:

1) Belátjuk, hogy 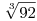$\root3\of{92}$ és -11 nem gyökei az egyenletnek, s ezért a gyökökhöz ezt az egyenletet vizsgáljuk:

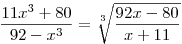
$\frac{11x^{3}+80}{92-x^{3}}=\root3\of{\frac{92x-80}{x+11}}$

2) Belátjuk, hogy a bal oldalon álló függvény a jobb oldalon álló inverze. A derékszögű koordinátarendszerben e két fv. grafikonja az y=x egyenesen metszi egymást.

3) A jobb (vagy a bal) oldalon álló kifejezést x - szel egyenlővé tesszük és a rendezések után ezt kapjuk:

x⁴+11x³-92x+80=0

4) Feltesszük, hogy van egész gyök. A szóba jövő egész gyökök a konstans tag osztói, ezért behelyettesítésekkel hamar kijön, hogy a gyökök: -10,-4,1 és 2.

Előzmény: [661] Blinki Bill, 2011-08-11 20:39:23

[664] Blinki Bill	2011-08-12 08:14:57
Köszönöm a megoldásaidat, ötleteidet. Élő versenyen (nem levelezős), ahol nem használhatok programot, ott hogyan oldom meg a 10-ed fokú egyenletet? Blanka
Előzmény: [663] Róbert Gida, 2011-08-12 01:09:50

[663] Róbert Gida	2011-08-12 01:09:50
B4360 Pontosan k=2^a*5^b alakú számok lesznek jók. Érdekes feladat.
Előzmény: [661] Blinki Bill, 2011-08-11 20:39:23

[662] Róbert Gida

2011-08-12 00:13:30

B4358 Feladat nem írja (miért is írná), de csak a valós megoldásokat keressük (köbgyökvonás a komplexeknél már nem is egyértelmű). Az egyik tagot átviszem a másik oldalra, köbre emelem, hogy eltűnjön a köbgyök, rendezem, kapok egy 10-edfokú egyenletet:

1423*x¹⁰+14561*x⁹+3648*x⁷+341520*x⁶+2547264*x⁴+291840*x³-71127296*x+67927040=0 (Mathematica szerint) ennek -10,-4,1,2 gyöke, és a feladatnak is (ellenőrzés). A maradó polinom hatodfokú: g(x)=1423*x⁶-1092*x⁵+12012*x⁴+2432*x³+100464*x²+87360*x+849088. Ennek már nincs valós gyöke: |x|<1-re a konstans tag miatt pozitiv g(x), míg |x|>1-re: 1423*x⁶ $\ge$ 1092*x⁵, 12012*x⁴ $\ge$ -2432*x³, 100464*x² $\ge$ -87360*x, egyenlőtlenségeket használva: g(x)>0 itt is.

Előzmény: [661] Blinki Bill, 2011-08-11 20:39:23

[661] Blinki Bill

2011-08-11 20:39:23

Sziasztok!

Feltenné vki a B.4358. és B.4360. feladatok megoldását?

Köszönöm: Blanka

[660] Lóczi Lajos	2011-08-10 16:28:48
Mathematica 7-ben ha a feladatkitűzésnek megfelelően írjuk be a képleteket, akkor egy bonyolult logikai kombinációt ad ki eredményül, amelyről kideríthetjük, hogy azonosan igaz. Ám ha a konklúzióbeli egyenlőtlenség tagadását írjuk be, indirekt bizonyítás-szerűen, akkor a Reduce pár másodperc alatt kiadja, hogy "azonosan hamis".
Előzmény: [659] Róbert Gida, 2011-08-09 00:27:07

[659] Róbert Gida

2011-08-09 00:27:07

Nézzük meg tudja-e oldani a Mathematica az A jelű feladatot:

a = (b*c*d - b - c - d)/(1 - b*c - b*d - c*d);

Timing[FullSimplify[(a + b)*(c + d) + (a + d)*(b + c) >= 4*Sqrt[(1 + a*c)*(1 + b*d)], a > 0 && b > 0 && c > 0 && d > 0]]

{21.965 Second, True}

Húha, megdolgozott a Mathematica a válaszért. Kicsit segítettem is neki, ha az "a"-t nem fejezem ki, akkor nem bizonyítja be, visszaadja az eredetit. Az persze kérdéses, hogy minden esetben szabályos-e ez, azaz amivel leosztok az nem nulla, esetleg b-vel, c-vel, d-vel eljátszhatom ezt, ha "a"-val nem.

Előzmény: [657] Tibixe, 2011-07-01 14:05:57

[658] Janosov Milán	2011-08-03 00:57:06
Valaki tudja, az utolsó mérési feladat fura statisztikájának mi a magyarázata?

[657] Tibixe

2011-07-01 14:05:57

Elég rögtön használni a számtani-mértani egyenlőtlenséget, homogenizálni és átrendezni.

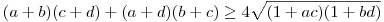
$(a+b)(c+d)+(a+d)(b+c) \ge 4\sqrt{(1+ac)(1+bd)}$

A számtani és mértani közép közti egyenlőtlenség miatt $4\sqrt{(1+ac)(1+bd)} \le 4\frac{1+ac+1+bd}{2}=4+2ac+2bd$ . Ezért erősebb állítás, hogy

(a+b)(c+d)+(a+d)(b+c) $\ge$ 4+2ac+2bd

Kifejtve és kivonva:

ad+bc+ab+cd $\ge$ 4

A feltétellel szerint a+b+c+d=abc+abd+acd+bcd és itt mindkét oldal pozitív, tehát utóbbi két oldalával ekvivalens átalakításként szorozhatjuk az állítást:

(a+b+c+d)(ad+bc+ab+cd) $\ge$ 4(abc+abd+acd+bcd)

A zárójeleket felbontva és nullára rendezve:

a²b+a²d+ab²-2abc-2abd-2acd+ad²+b²c+bc²-2bcd+c²d+cd² $\ge$ 0

Ezt átírva:

(a+c)(b-d)²+(b+d)(a-c)² $\ge$ 0

Ez nyilván teljesül, mert nemnegatív teljes négyzetek nemnegatív együtthatós polinomja is nemnegatív.

Előzmény: [655] sakkmath, 2011-07-01 08:44:32

[656] sakkmath	2011-07-01 09:01:36
Az előbbi név helyesen: Schwarz.
Előzmény: [655] sakkmath, 2011-07-01 08:44:32

[655] sakkmath

2011-07-01 08:44:32

A KöMaL 2011/5-ös, májusi

számában megjelent

A.536. feladat egyik megoldása:

Már regisztráltál?
Új vendég vagy?