Fórum: Lejárt határidejű KÖMAL feladatokról

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49]

Szeretnél hozzászólni? Jelentkezz be.

[734] Róbert Gida

2013-01-15 21:28:38

Decemberi lejárt B4500.: "Útmutatás: Igen. Bizonyítsuk be, hogy f(1)=1."

Bizonyítást nem találunk hozzá, de mindegy is, mert nem igaz: legyen g(n)=2*n²+2*n-1. Ekkor g(1)=3; és megfelelő polinom!

Prímek meg egyáltalán nem kellenek a bizonyításhoz, elég azt belátni, hogy f_i(n) $\equiv$ 1mod n, illetve nálam: g_i(n) $\equiv$ -1mod n.

[733] w

2012-12-16 18:00:47

Úgy tűnik, hogy nem fogják a honlapra felrakni az A. 573. feladat megoldását, pedig relatívan egyszerű volt (a leírása a legnehezebb rész).

Valaki elmondaná-e az A. 572. megoldását?

[732] vogel	2012-11-26 02:26:59
Gondolom nem. Csak nem értettem, miért van útmutatás, ha alatta van a megoldás. :) De már értem.
Előzmény: [731] vogel, 2012-11-26 02:25:13

[731] vogel	2012-11-26 02:25:13
Ezek az útmutatások, amik a megoldások felett vannak, megjelennek az újságban is?

[730] w

2012-11-24 23:41:27

A honlapinál egyszerűbb megoldás B.4477-re:

A feltétel szerint A és B rajta van a PQ Apollóniusz-körén; Thálesz-tétel megfordítása szerint R is rajta van. A PRQ< szögfelezője messe PQ-t A'-ben -- szögfelezőtétel miatt A'=A, innen adódik a bizonyítandó állítás. (Nem töltök fel ábrát, mert könnyű fejben elképzelni.)

Nagyon szépen, egyszerűen kijön C.1139. (Legalább mekkora átfogójú az a derékszögű háromszög, amelynek kerülete k?):

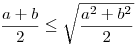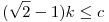A szokásos jelölésekkel $\frac{a+b}2\le\sqrt{\frac{a^2+b^2}2}$ , azaz $\frac{k-c}2\le\frac{c}{\sqrt2}$ , innen $(\sqrt2-1)k\le c$ , ezzel készen is vagyunk, mert egyenlőség a=b esetén fennállhat.

[729] m2mm	2012-11-24 21:19:09
Több pont helyett most néha adnak különdíjat általánosításra, bár ahogy ezt elnézem ez változik évenként hogy mire adnak pontosan(általánosítás/szép megoldás/egyedüli megoldó/Fair Play).
Előzmény: [728] w, 2012-11-24 19:47:44

[728] w	2012-11-24 19:47:44
Több pont általánosításokra? Jó lehetett. Persze, annak is van értelme, hogy nincs extra pont, pl. a B-ben könnyebb egy egyszerűbb példát általánosítani, mint egy összetettebb példa megoldásával megszerezni ugyanazt a pontszámot. Én mondjuk ennek ismeretében mégis hozzáírom a megjegyzéseket, mert szerintem érdemes a javítóval tudatni, hogy a példát kissé továbbgondoltam. Kevés időt vesz igénybe, nem sülhet ki rosszul, és hát nem érzem úgy, hogy "hiányos" a dolgozat.
Előzmény: [727] Róbert Gida, 2012-11-24 15:46:52

[727] Róbert Gida

2012-11-24 15:46:52

"Természetesen lehet általánosítani, Megjegyzés rovatba :)"

Igen, de nem kapsz rá plusz pontot. Ami nagyon is jól van, a mi időnkben még volt olyan, hogy valaki az eredetileg 5 pontos feladatra általánosítások miatt 8 pontot kapott.

Előzmény: [726] w, 2012-11-24 12:34:57

[726] w

2012-11-24 12:34:57

Szerintem azért így tűzték ki a feladatot, mert ilyen formában nehezebb rájönni a megoldásra, első nekifogásban valamilyen egyszerű módszerrel (szögszámítás, Thálesz, Pit.) állok hozzá (magam nevében beszélek). Több adattal több felesleges dolog jön ki, amibe belegabalyodhatok. Végül egyszerűen kijött, Apollóniusz-körrel. Természetesen lehet általánosítani, Megjegyzés rovatba :)

[725] m2mm

2012-11-23 16:28:38

Ha A,B,C,D pontok ilyen sorrendben egy egyenesen vannak és harmonikus pontnégyest határoznak meg, akkor tetszőleges I pontra a síkon(leszámítva AB egyenes pontjait), pontosan akkor lesz 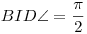$BID\angle=\frac{\pi}{2}$ , ha AIB $\angle$ =BIC $\angle$ . Ez belátható pl. szinusz-tételekkel, ujjgyakorlat.

Így valójában a feladatban P lehet bármely mást pont AB oldalon és Q az AP.BQ=AQ.BP feltétellel megadott pont(AB egyenesen), akkor is fennáll a szögfelező tulajdonság, magyarán van egy kis fölös információ a feladatban.

Előzmény: [723] Erben Péter, 2012-11-23 10:24:07

[724] Erben Péter

2012-11-23 14:49:21

Javítva:

A AP^.BQ=AQ^.BP feltétel így is írható:

$\frac{AP/PB}{AQ/QB}=-1$

Előzmény: [723] Erben Péter, 2012-11-23 10:24:07

[723] Erben Péter

2012-11-23 10:24:07

Egy észrevétel a B.4477. egy lehetséges hátteréről.

A AP^.BQ=AQ^.BP feltétel így is írható: $\frac{AP/PB}{AQ/QP}=1$ . Erről - ha a pontok lehetséges sorrendjét elemezve a szakaszokat előjeles hosszal jellemezzük - a kettősviszony juthat eszünkbe: (ABPQ)=-1.

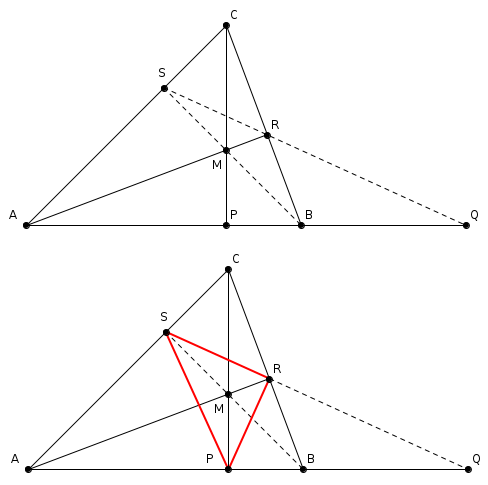
Tehát A és B harmonikusan választja el P-t és Q-t, amiből az következik, hogy Q az ábrán látható módon (szaggatott vonalak) szerkeszthető. (Az MRCS négyszög szemközti oldalegyeneseinek metszéspontja A és B, átlói pedig a P és Q pontokban metszik az AB egyenest.)

Végül arra kell csak emlékezni, hogy a PRS talpponti háromszög belső szögfelezői az ABC háromszög magasságvonalai, innen egyszerűen következik az eredeti feladat állítása.

[722] valaki akit úgyis ismersz	2012-11-14 20:48:09
Megoldotta vki az A.569.-et?

[721] valaki akit úgyis ismersz	2012-11-14 20:42:41
Tudomásul vettem.
Előzmény: [720] Róbert Gida, 2012-11-14 20:14:48

[720] Róbert Gida	2012-11-14 20:14:48
Az számít, hogy mit küldtél be, azt pedig mi nem tudhatjuk. Amúgy, ha nagyon szigorúan nézném, akkor 0 pontos is lehetne a megoldásod, mert nem a feladott példát oldottad meg. Érettségin például simán kaphatsz ilyenért nulla pontot.
Előzmény: [719] valaki akit úgyis ismersz, 2012-11-14 17:14:16

[719] valaki akit úgyis ismersz	2012-11-14 17:14:16
Elnézést, kissé félreírtam; mm2m: valóban szorzás nem összeadás; továbbá a törtbecslésnél szigorú az egyenlőtlenség, mint a háromszög-egyenlőtlenségben, nincs 1 pont levonás.
Előzmény: [716] m2mm, 2012-11-14 00:43:58

[718] Fálesz Mihály	2012-11-14 09:11:48
Érdemes megrajzolni az ABC, ABP, BCP, CAP háromszögek beírt köreit.
Előzmény: [716] m2mm, 2012-11-14 00:43:58

[717] Róbert Gida	2012-11-14 02:10:06
$<\frac 52$ -et kellett bizonyítani. 1 pont levonás.
Előzmény: [714] valaki akit úgyis ismersz, 2012-11-13 22:07:01

[716] m2mm

2012-11-14 00:43:58

A.570. (vázlatos)

AC₁(P)PB₁(P) pontosan akkor érintőnégyszög, ha AB-AC=PB-PC(ismert, de érintőszakaszok felírásával triviális). P tehát az a pont, amin áthaladnak azon hiperbolaágak, melyekhez tartozó fókuszpontok ABC háromszög két csúcsa, és áthaladnak a harmadik csúcson. P megvan konstruálva, szerkesztés az már csúnyább, de a hiperbolaágak egyenlete felírható és ezekből a metszéspont is megvan... A kérdés, hogy számolás nélkül valaki megtudja-e szerkeszteni?

[715] m2mm

2012-11-14 00:18:15

Hát na ne már egy egyenlőtlenség-feladat nem attól lesz szép, hogy kipróbálunk egy Cauchy-t és hopp, kijön belőle még egy lépéssel, hanem inkább tudatosan keressünk köztes becslést(mint a hiv. megoldás is) illetve a kifejezés, mint fv. viselkedéséből szűrünk le infót. Persze ez gusztus dolga.

Ja, az első egyenlőtlenségedben a két gyökös kifejezést nem összeadod, hanem összeszorzod, erre figyeljünk, az ember ebben hiába keres Cauchy-t.

Előzmény: [714] valaki akit úgyis ismersz, 2012-11-13 22:07:01

[714] valaki akit úgyis ismersz

2012-11-13 22:07:01

A szépség a feladatban az, hogy egyszerű módon is megoldható, ráadásul durva becslésekkel. Cauchy-egyenlőtlenség szerint 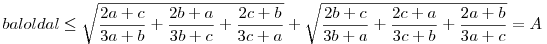$bal oldal \le \sqrt{\frac{2a+c}{3a+b}+\frac{2b+a}{3b+c}+\frac{2c+b}{3c+a}}+\sqrt{\frac{2b+c}{3b+a}+\frac{2c+a}{3c+b}+\frac{2a+b}{3a+c}}=A$ .

Továbbá pl.

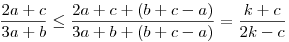
$\frac{2a+c}{3a+b}\le\frac{2a+c+(b+c-a)}{3a+b+(b+c-a)}=\frac{k+c}{2k-c}$

,ahol k=a+b+c (törtek becslésére vonatkozó tétel, $\Delta$ -egyenlőtlenség). Tehát

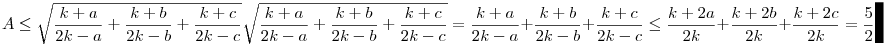$A\le\sqrt{\frac{k+a}{2k-a}+\frac{k+b}{2k-b}+\frac{k+c}{2k-c}}\sqrt{\frac{k+a}{2k-a}+\frac{k+b}{2k-b}+\frac{k+c}{2k-c}}=\frac{k+a}{2k-a}+\frac{k+b}{2k-b}+\frac{k+c}{2k-c}\le\frac{k+2a}{2k}+\frac{k+2b}{2k}+\frac{k+2c}{2k}=\frac52$ .

Azaz készen vagyunk. A korlát élességéről némi határértékszámítással győződhetünk meg, ha a=b és c egészen kicsi.

[713] nadorp

2012-11-13 15:54:42

A bizonyítás első része deriválás nélkül is megy:

(2a+c)(2b+c)=c²+2ac+2bc+4ab=(a+b+c)²-(a-b)²

(3a+b)(3b+a)=3a²+10ab+3b²=4(a+b)²-(a-b)²

Tehát, felhasználva, hogy 2(a+b)>a+b+c

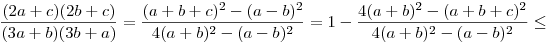
$\frac{(2a+c)(2b+c)}{(3a+b)(3b+a)}=\frac{(a+b+c)^2-(a-b)^2}{4(a+b)^2-(a-b)^2}=1-\frac{4(a+b)^2-(a+b+c)^2}{4(a+b)^2-(a-b)^2}\leq$

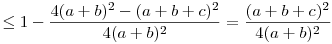
$\leq1-\frac{4(a+b)^2-(a+b+c)^2}{4(a+b)^2}=\frac{(a+b+c)^2}{4(a+b)^2}$

Előzmény: [712] m2mm, 2012-11-13 13:42:08

[712] m2mm

2012-11-13 13:42:08

A.571.

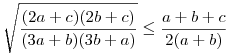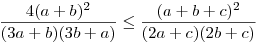Először $\sqrt{\frac{(2a+c)(2b+c)}{(3a+b)(3b+a)}}\le \frac{a+b+c}{2(a+b)}$ -t látom be. Négyzetre emelve és egy oldalra hozva a c-t tartalmazó tényezőket az ekvivalens $\frac{4(a+b)^2}{(3a+b)(3b+a)}\le \frac{(a+b+c)^2}{(2a+c)(2b+c)}$ (*) a bizonyítandó. Rögzített 0<a,b-re tekintsük f_a,b: R⁺->R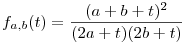⁺ $f_{a,b}(t)=\frac{(a+b+t)^2}{(2a+t)(2b+t)}$ függvényt.

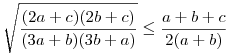$f'_{a,b}(t)=\frac{2(a+b+t)(2a+t)(2b+t)-(a+b+t)^2(a+b+t)^2}{(2a+t)^2(2b+t)^2}\le 0$ , mivel ez ekvivalens 2(a+b+t)(2a+t)(2b+t)-2(a+b+t)²(a+b+t) $\le$ 0-val, (2a+t)(2b+t) $\le$ (a+b+t)²-tel, 0 $\le$ (a-b)²-tel. Tehát f_a,b monoton csökkenő, továbbá a+b>c, így f_a,b(c) $\ge$ f_a,b(a+b). Behelyettesítve (*) adódik. Tehát $\sqrt{\frac{(2a+c)(2b+c)}{(3a+b)(3b+a)}}\le \frac{a+b+c}{2(a+b)}$ . A másik két tagra is felírva a hasonlóan adódó egyenlőtlenséget

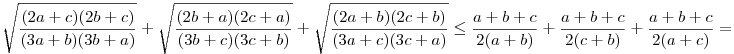
$\sqrt{\frac{(2a+c)(2b+c)}{(3a+b)(3b+a)}}+\sqrt{\frac{(2b+a)(2c+a)}{(3b+c)(3c+b)}}+\sqrt{\frac{(2a+b)(2c+b)}{(3a+c)(3c+a)}}\le \frac{a+b+c}{2(a+b)}+\frac{a+b+c}{2(c+b)}+\frac{a+b+c}{2(a+c)}=$

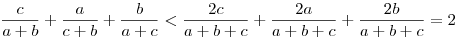$=\frac{3}{2}+\frac{1}{2}(\frac{c}{a+b}+\frac{a}{c+b}+\frac{b}{a+c})<\frac{5}{2}$ , mivel $\frac{c}{a+b}+\frac{a}{c+b}+\frac{b}{a+c}< \frac{2c}{a+b+c}+\frac{2a}{a+b+c}+\frac{2b}{a+b+c}=2$ .

[711] m2mm	2012-10-12 13:39:38
Szándékos is lehetett, letesztelni ki az akit lehet tanítani, nem csak vegetál szakkörökön, illetve ki az aki a nehéznek tűnő feladatokat bemisztifikálja és esélytelen emiatt egy IMO 3 vagy 6-ra...
Előzmény: [710] Róbert Gida, 2012-10-12 00:56:00

[710] Róbert Gida

2012-10-12 00:56:00

Lejárt A567. megoldása.

Ritkán ad a szerkesztő (Kós Géza) segítséget egy akkor még élő feladathoz. Az olimpiai szakkör második feladatának (1988/6) megoldásában ugyanaz a trükk van, mint az egyébként pont a Pelikán által kitűzött A567-ben.

Egyszerre oldom meg az a,b, részét a feladatnak, legyen e=5 vagy 3. A feladat szerint a|b²-e, és b|a²-e és a,b relatív prímek, így ab|a²+b²-e is teljesül, sőt ez megfordítva is igaz (kivéve az, hogy relatív prímek lesznek). Nagyszerű, a két oszthatósági feltételből egyet csináltam.

Ha ab|a²+b²-e, akkor a²+b²-e=kab teljesül valamilyen k egészre (k lehet negatív is). Az a,b szerepe szimmetrikus, így feltehető, hogy a $\le$ b. Rendezve: b²-kab+a²-e=0, azaz x=b megoldása az x²-kax+a²-e=0 másodfokú egyenletnek. Végtelen leszállás (méthode de descente infinie) következik, majd felszállás.

Tegyük fel, hogy a>2 teljesül. Ha az egyenletnek az egyik megoldása 'b', akkor a másik b₂=ka-b (gyökök és együtthatók közti összefüggés) és a,b₂-re teljesül, hogy a²+b₂²-e=kab₂, sőt a,b₂ relatív prímek, hiszen lnko(a,b₂)=lnko(a,ka-b)=lnko(a,b), továbbá b₂ egész (trivi), és pozítiv, hiszen $b_2=\frac{a^2-e}{b}>0$ , mert a²-e $\ge$ 9-5=4>0 és b>0. Már csak az kell, hogy "kisebb" megoldást találtunk, valóban: 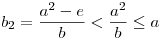$b_2=\frac{a^2-e}{b}<\frac{a^2}{b}\le a$ (utóbbi azért, mert a $\le$ b volt). Azaz a (b₂,a) pár megoldás, ahol b₂<a, így az (a,b) párnál a rendezésben kisebb megoldást kaptunk.

Leszállás addig működik, amíg az a>2 feltétel teljesül. Mikor akadunk el e=3 esetben: ha a=1, akkor b=1 vagy b=2, míg az a=2 eset nem ad megoldást. Így (még a (2,1) páron kívül) nincs más megoldás, hiszen a felszálláshoz szükséges b>2 feltétel egyikre sem teljesül. Ha e=5, akkor a=1 esetén b=1,2,4 és a=2 nem ad megoldást. Végtelen felszállás működik, de csupán az (1,4) párra, hiszen ott b>2. Figyeljük meg, hogy k értéke egy sorozat mentén konstans, itt k=3. Azaz az összes megoldás (1,1),(1,2) és legyen a₀=1;a₁=4;a_n=3a_n-1-a_n-2, ekkor (a_n,a_n+1) megoldás, illetve ezek felcserélésével kapott párok. És nincs több megoldás. Ehhez még elsüthetjük azt, hogy a fel/leszállás adott megoldásból kiindulva egyértelmű, hiszen a másodfokú egyenletnek két gyöke van.

Már regisztráltál?
Új vendég vagy?