| [814] w | 2013-05-15 17:44:22 |
 De legalább elemi.
Egyébként ha már kétszer is hivatkozik feladat a megjegyzésben leírt cikkre, jó volna elektronikusan is hozzáférni. Tudjátok-e, hogy kapható-e olyan régi Kömal?
|
| Előzmény: [813] Róbert Gida, 2013-05-15 17:11:13 |
|
|
| [812] w | 2013-05-14 16:30:01 |
 Áprilisi feladatokból.
A.587 nem valami ügy (feltéve, hogy nem szúrtam el semmit). Vázlatosan: lebetűzzük, hogy ai között melyik mod 4 maradéknak mennyi a gyakorisága, kifejezzük belőle az összeghalmaz maradékait, és a kapott egyenletrendszert "ügyesen" megoldjuk. Szokatlanul egyszerű az eredmény, az jön ki, hogy n egy negyedik hatvány kell legyen, és ha a maradékok rendben vannak, akkor az összegek eltérése elintézhető, az ai számoknál minden új számot az összes többi összegénél nagyobbnak választjuk.
B.4540. Ez egy érdekes feladat. Az n=2 esetnél k=1 (könnyű), ezért adott n-re k=[n/2] elérhető (párbaállítás). Ennél több nem lehet. Valóban, egy adott rab tévedési esélye 1/2, ezért minden lehetséges sapkakiosztásra eljátszva a stratégiát n.2n tipp lesz, és belőle n.2n-1 talált. Skatulya-elv miatt lesz olyan kiosztás, melyre max. n/2 jó tipp van, tehát készen vagyunk.
B.4541. Vegyünk három pontot: (xi,xi2,xi3) (i=1,2,3). A rájuk illeszkedő sík egyenlete a1x+a2y+z+a0=0 alakú (nyilván nem vízszintes), behelyettesítve a három pont koordinátáit xi3+a2xi2+a1xi+a0=0 (i=1,2,3). Ez olyan gyanús polinom alakú (persze, mert úgy írtam fel a sík egyenletét :-) ). Ez a polinom nem más, mint p(x)=(x-x1)(x-x2)(x-x3). Tudjuk, hogy az {1;2;...;100} tartományon minden más x-re a hozzá tartozó pont e sík felett van, már ha az a sík K része. Akkor z>-(a1x+a2y+a0) vagy pont fordítva. Átrendezve p(x)>0 vagy p(x)<0 minden x {1;2;...;100}\{xi:i=1,2,3} esetén. A gyöktényezős felbontásból ez összesen 196 módon lehet. Továbbá mivel K minden lapja ily módon háromszög, 294 él és (Euler) 100 csúcs lesz. {1;2;...;100}\{xi:i=1,2,3} esetén. A gyöktényezős felbontásból ez összesen 196 módon lehet. Továbbá mivel K minden lapja ily módon háromszög, 294 él és (Euler) 100 csúcs lesz.
|
|
| [811] w | 2013-05-14 16:07:25 |
 Szerintem biztos egyetemi anyagra van szükség, és hivatalos megoldást nem fognak felrakni. Ettől függetlenül kíváncsi volnék a megoldásodra, vagy akár egy vázlatra (a megértéshez van nálam szakirodalom).
|
| Előzmény: [810] nadorp, 2013-05-13 21:08:59 |
|
| [810] nadorp | 2013-05-13 21:08:59 |
 A588-ra van viszonylag egyszerű megoldásom, de egyetemi anyagot - véges testek, testbővítés - is használ. Várnék a hivatalos megoldásra, lehet, hogy van elemi bizonyítás is.
|
| Előzmény: [807] w, 2013-05-11 09:35:56 |
|
|
| [808] w | 2013-05-13 16:38:26 |
 A B.4515-ről szóló hozzászólásommal valami baj van, nem tudom, hogy ezt Ti is látjátok-e. A k*szin* szóhoz nem raktam semmiféle linket sem, viszont érdekes módon valamilyen robot egy reklámoldalt rakott be hozzá. Ha pl. válaszolunk rá, akkor pedig a link eltűnik. A jelenséget érdemes volna eltüntetni. Válaszokat előre is köszönök.
|
| Előzmény: [806] w, 2013-05-06 13:39:47 |
|
| [807] w | 2013-05-11 09:35:56 |
 A B4539 szép megoldásáért (ha van), vagy valamelyik A-jelű feladat megoldásáért cserébe felraknám a B4540, B4541 vagy A587 megoldását.
|
|
| [806] w | 2013-05-06 13:39:47 |
 A B.4515 feladat mintájára kitűzném a következő feladatot.
Egy kaszinó egy speciális új játékautomatát vett. Zsetonnal működik, és a zsetont előre meg kell venni adott áron. A következőképpen működik. Zseton bedobása után egy legfeljebb két körös játék indul meg. Az automata véletlenszerűen választ egy egész számot 1 és n között (n rögzített), és megmutatja. Ha a látható számmal elégedett a játékos, felveszi nyereményét, ami a látható számmal megegyező számértékű pénz, és a játék véget ér. Ha a játékos szerencsésnek érzi magát, akkor még egy zsetont bedob, folytatva a játékot; a gép újra generál egy számot 1-től n-ig, és ekkor a nyeremény a két szám szorzata lesz. Melyik az az xn szám, amely esetén ha a zseton ára xn, akkor a kaszinó várható bevétele 0 lesz? (+ Ha lehet, adjuk meg xn-et rekurzívan és explicite is.)
|
| Előzmény: [768] w, 2013-03-14 15:25:38 |
|
| [805] w | 2013-04-29 18:21:08 |
 Jó, hogy így egyedül vezetem a témát. Kíváncsi volnék, még talán marcius8 kedvéért is, hogy az A.585-ös szép "magyar passziánsz"-remineszenciát hogy lehetett megfogni (ugyebár ő terjesztette elő a problémakört). Előre is köszönöm az esetleges válaszokat!
|
|
| [804] w | 2013-04-28 10:45:08 |
 A C.1162 feladat kiírt megoldása hibás. Idézem: "Tehát a paralelogramma összes szöge hegyesszög."
Emellett még hibás a C.1145 feladat hiv. megoldása: "Írjuk fel két tetszőleges négyzetszám különbségét. Ez valahány egymás utáni négyzetszám összege lesz."
Aki alaposan meggondolta a feladatot, annak ezek az elírások nem okoznak gondot, de biztosan akad olyan, akinek igen nehéz megérteni a megoldást, ha kíváncsi, hogy a kitűzők hogyan oldották meg.
|
|
| [803] w | 2013-04-23 21:34:17 |
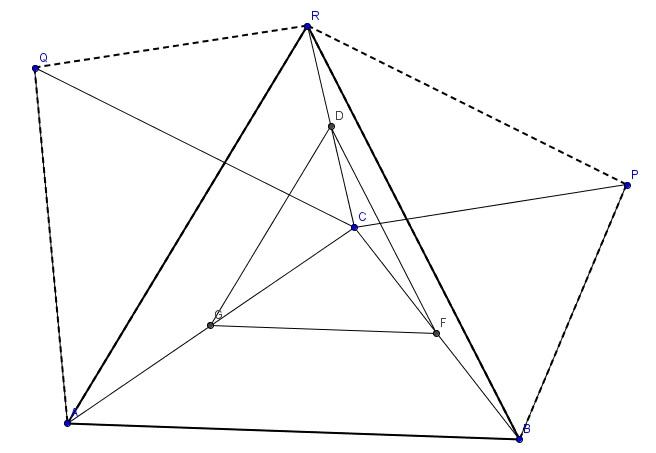
 B.4530 megoldása szebben.
Használva az ábra jelöléseit, nagyítsuk FGD-t C körül kétszeresére --> BAR háromszög. Itt CPRQ paralelogr., hisz kposan tükrös. Azt fogjuk igazolni, hogy ABR hasonló BCP-hez, egy további stratégiával: azt mutatjuk meg, hogy BR:BA=BP:BC és AR:AB=AQ:AC. Vegyük észre, hogy ABC, RBP és ARQ hasonló háromszögek! Pl. ABC és ARQ hasonló: AQR<=ACB< (szögszámítás) és AQ:QR=AQ:CP, ami AC:CB a hasonlóság miatt. Ugyanígy ABC hasonló RBP, tehát készen is vagyunk.
|
 |
|
| [802] w | 2013-04-23 17:42:34 |
 C. 1160. Mennyi a maradék, ha a 20122013+20132012 összeget elosztjuk 2012.2013-mal?
A hiv. megoldás binomiális tétellel készült. A versenykiírás szerint azonban "egy hónapon belül a kisebb sorszámú feladatokat ajánljuk a fiatalabb versenyzőknek". Ennek megfelelően az általános iskolás megoldás:
20132012=(2012+1)20132011=2012.20132011+20132011 20132011 (mod 2012.2013), 20132011 (mod 2012.2013),
és hasonló lépésekkel 20132012 20132011 20132011 ... ... 2013 (2012.2013), ugyancsak 2013 (2012.2013), ugyancsak
20122013=20122.20122011=(2011.2013+1).20122011 20122011 20122011 ... ... 2012 (mod 2012.2013). 2012 (mod 2012.2013).
Vagyis a maradék 2012+2013=4025.
|
|
|
|
| [799] m2mm | 2013-04-19 20:12:23 |
 Mondjuk olvasd el ennek a cikknek az alján levő három estere való írását:
http://www.komal.hu/cikkek/dandelin/dandelin.h.shtml
Utána mondjuk lásd be, hogy a kúp C csúcsának az ellipszis síkjára vett merőleges vetülete az AB nagytengelyen van, innen pedig azt lásd be, hogy CAB háromszög minden oldalát érinti a cikkben leírt beírt gömb. Innen B.4450. és adódik(persze itt nem csak az egyik hiperbolaíven lesznek pontok, mert a két fókuszpont bármelyikére bármelyik oldalra vehetjük a beírt gömböt), hogy a kérdéses pontok halmaza egy hiperbolán van, minek síkja merőleges az ellipszisére, és fókuszpontjai az ellipszis nagytengelyének végpontjai etc.
A többi kúpszeletre, ha érdekel nézd végig hasonlóan.
|
| Előzmény: [798] w, 2013-04-18 08:26:04 |
|
|
| [797] m2mm | 2013-04-18 01:03:39 |
 Ahogy én tapasztaltam A és B példák közti egyik fő különbség, hogy A-nál valami nagyobb, hatásosabb eszközt/módszert tudsz felfedezni magadtól/gyakorolni, míg a B-példák puzzle-ként kijönnek ált. max. 2 lépésben ha az ismert apró trükköket helyes sorrendben kihasználod.
Mostanában nincs időm nagyon A-kat nézegetni, B-k meg már nem mondanak újat, így
B.4525-öt sem oldottam meg, azaz nem tudom eldönteni A-ba való-e, ránézésre nem. Pláne mert a konstrukció(legalábbis a tied) nem igényel komolyabb hátteret, mint ld. pl. A.524.
Az általad említett A.542.-re én teljesen különböző megoldást találtam, de az is és a hiv. megoldás is azt mutatja hogy váratlanul "egyszerű" a megoldása általában egy komb. példának.
Nehézségre A.584. se valami nagy ügy, de Dandelin-gömb és B.4450 alap hozzá, B-be nem berakható. Mondjuk B.4450. előkerül A.570 megoldásánál is (bár vele csak az jön ki, hogy mi a megszerkesztendő pont valójában, onnan kell kicsi számolás a szerkesztéshez, de annak a feladatnak amúgy sem a szerkesztés kéne hogy legyen a lényege, csak a pont ily módon való meghatározása, de ez csak egyéni vélemény)
De a megoldáshoz nem kell ezeket tudni, arra is van az A-példa, hogy aki nem ismeri az magától rájöjjön ezekre. Mint ahogy pl. a Sawayama-lemmát se kell ismerned, az A-példák arra vannak hogy részeredményként belásd, aztán hiv. megoldásból tudod, hogy ezt így hívják.
|
| Előzmény: [796] w, 2013-04-17 19:33:06 |
|
|
| [795] w | 2013-04-14 19:59:20 |
 Senki? Fontos kiindulási adat, hogy az a1, a2, a3, a4 sorozat és az A1, A2, A3, A4 sorozat azonosan rendezett, enélkül talán nem is igaz az egyenlőtlenségem (?).
|
| Előzmény: [793] w, 2013-04-11 07:21:56 |
|
|
| [793] w | 2013-04-11 07:21:56 |
 A.588 (?) könnyítés:
Igazoljuk, hogy 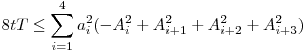 , ahol a két négyszög oldalai azonosan rendezettek. , ahol a két négyszög oldalai azonosan rendezettek.
|
|
| [792] w | 2013-04-11 07:18:20 |
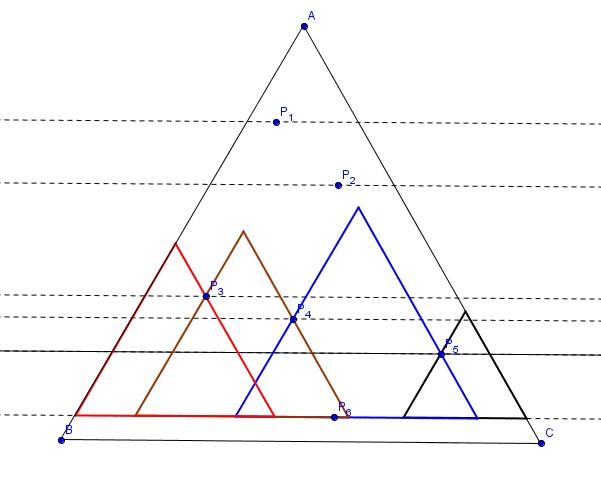
 De a mostani B.4525 is mehetett volna az A-ba. Nehéz konstrukciót találni. A következő pl. szerintem jó:
Rekurzív. Tfh. 2n-1 3-szög lefedi az (n-1) felvett belső pontú 3-szöget. Az n-edik Pn ponton át ||-t húztunk T oldalával (pn), a levágott 3-szög lefedhető (2n-1)-gyel. A maradó réteget úgy fedjük le, hogy meghosszabbítjuk a lefedők oldalait T oldaláig. A kapott háromszögek ha tartalmazzák Pn-et, húzzunk Pn-nel még két T-oldalirányban ||-t. A legnagyobb kétféle ilyet vegyük, mint új háromszög. Ez jó is lesz, mert lefedik a pn T-be eső részét a generálás módja miatt, és így a 3-szögek állásából lefedik az új "réteget".
Az ellenpélda n db pont egy T oldalával nem || egyenesen, ki-ki lássa be.
|
 |
| Előzmény: [791] w, 2013-04-08 16:32:23 |
|
| [791] w | 2013-04-08 16:32:23 |
 Egyetértek, ingadozó nehézségű A-jelű problémák vannak. Szerintem azt a feladatot azért tűzték ki, hogy kiszűrjék azokat, akik bemisztifikálják az A-feladatokat. Egyébként meg nem természetes, hogy most már négy olyan feladat is volt, melyre egyáltalán nem született megoldás. (Igaz, a mezőny sem olyan erős.) Sok olyan B-jelű 6 pontos feladatot látni, amely bőven méltó lenne az A-pontversenybe: B.4510, B.4511, B.4520, B.4521.
|
| Előzmény: [790] HoA, 2013-04-08 14:02:31 |
|
| [790] HoA | 2013-04-08 14:02:31 |
 Tudja valaki miért volt A.581 "A" feladat? Nekem a "Projektív geometria" téma [41] végén is leírt módon elég egyszerűnek tűnt.
|
|




 {1;2;...;100}\{xi:i=1,2,3} esetén. A gyöktényezős felbontásból ez összesen 196 módon lehet. Továbbá mivel K minden lapja ily módon háromszög, 294 él és (Euler) 100 csúcs lesz.
{1;2;...;100}\{xi:i=1,2,3} esetén. A gyöktényezős felbontásból ez összesen 196 módon lehet. Továbbá mivel K minden lapja ily módon háromszög, 294 él és (Euler) 100 csúcs lesz. 

 20132011 (mod 2012.2013),
20132011 (mod 2012.2013), 
