Fórum: Lejárt határidejű KÖMAL feladatokról

B.4643.' Léteznek-e olyan $\displaystyle n$ és $\displaystyle k$ egész számok, amelyekre $\displaystyle n^4-n^2-n=k^2-k+1$?

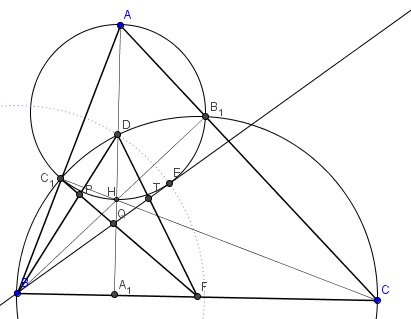
A.621. Az $\displaystyle ABC$ hegyesszögű háromszög magasságainak talppontjai rendre $\displaystyle A_1$, $\displaystyle B_1$, illetve $\displaystyle C_1$. A $\displaystyle BC$ oldal felezőpontja $\displaystyle F$. A $\displaystyle BCB_1C_1$ pontokon átmenő kör az $\displaystyle AA_1$ szakaszt a $\displaystyle D$ pontban metszi. Legyen $\displaystyle T$ az a pont a $\displaystyle DF$ szakaszon, amelyre a $\displaystyle BT$ egyenes érinti az $\displaystyle AB_1C_1$ kört. Messe a $\displaystyle C_1F$ szakasz a $\displaystyle BD$ és $\displaystyle BT$ egyeneseket $\displaystyle P$-ben, illetve $\displaystyle Q$-ban. Mutassuk meg, hogy a $\displaystyle DPQT$ négyszög érintőnégyszög.

Megoldás. $\displaystyle BT$ az $\displaystyle E$ pontban érinti $\displaystyle AB_1C_1$ kört, a magasságpont $\displaystyle H$. Ismert, hogy $\displaystyle AB_1HC_1$ húrnégyszög.

Egy, az érintőnégyszögek tételéhez hasonlóan belátható tétel (B.4639. rokona) szerint $\displaystyle DPQT$ pontosan akkor érintőnégyszög, hogyha $\displaystyle BD-FD=BQ-FQ$ (1).

Könnyű látni, hogy $\displaystyle FC_1B\angle=\beta$ és $\displaystyle AC_1B_1\angle=\gamma$, innen $\displaystyle FC_1B_1\angle=\alpha=C_1AB_1\angle$. Ebből leolvasható, hogy $\displaystyle F$ az $\displaystyle AB_1C_1$ körhöz $\displaystyle C_1$-ben húzható érintőre illeszkedik.

Kaptuk, hogy $\displaystyle QC_1=QE$ egyenlő hosszú érintőszakaszok. Ezzel (1) átalakítható:

$\displaystyle BD-FD=BQ-FQ=(BQ+QE)-(FQ+QC_1)=BE-FC_1.$

Mivel $\displaystyle FC_1=FD$, ezért csak annyit kell belátnunk, hogy $\displaystyle BD=BE$.

Invertáljunk a $\displaystyle B$ középpontú, $\displaystyle BE$ sugarú körre! Ekkor az $\displaystyle AB_1C_1$ kör invariáns marad, hisz merőleges az alapkörre, így $\displaystyle A$ és $\displaystyle C_1$, $\displaystyle B_1$ és $\displaystyle H$ helyet cserél. Ezért $\displaystyle AH$ egyenes képe $\displaystyle BB_1C_1$ kör lesz.

Az inverzióban $\displaystyle D\in AH$ képe a $\displaystyle BD$ egyenesen lesz, és a $\displaystyle BB_1C_1$ körön. Mivel $\displaystyle D$ képe $\displaystyle B$ nem lehet, ezért $\displaystyle D$ fixpont kell legyen. Vagyis $\displaystyle BD=BE$. Ezzel (1)-et beláttuk, készen vagyunk.

Tetszik az a meglátás, hogy a probléma ekvivalens azzal, hogy $\displaystyle BC$ oldal hatványvonala az $\displaystyle AB_1C_1$ körnek és $\displaystyle D$ pontnak.

Innen rövid befejezés kínálkozik a megoldásra.

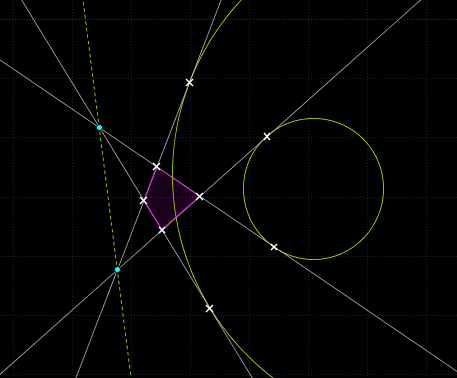
Az A621-hez egy lemma (az A613-as ha már nem jött ki vele):

Ha két körhöz a hatványvonalán ha felveszünk két pontot, akkor azokból ha érintőket húzunk, a megfelelő érintőegyenesek egy érintőnégyszög oldalai.

A megfordítása meg valami olyasmi, hogy ha az egyik pont nincs a hatványvonalon, akkor a másik pont egy hiperbolán mozog, ha érintőnégyszögeket akarunk kapni (a két körtől való távolságok különbsége állandó).

És akkor azt kell belátni, hogy a B és F pontok az $\displaystyle AB_1C_1$ és a D pont hatványvonalán fekszenek.

(nem biztos, hogy így a legegyszerűbb)

Ábra:

Egy megjegyzés a C. 1242. feladathoz. Nemcsak derékszögű, hanem bármilyen háromszögre érvényes a következő tétel. Az alábbi három állítás közül 1) az egyenes felezi a háromszög kerületét 2) az egyenes felezi a háromszög területét 3) az egyenes átmegy a beírt kör középpontján ha bármelyik kettő mint feltétel igaz, akkor a harmadik is, mint állítás igaz. A kitűzött feladatra vonatkozólag ez azt jelenti, hogy a megoldásként kapott „felező egyenes” is átmegy a háromszög beírható körének középpontján. A feladat speciális adataival ez kis számolással a fenti tétel ismerete nélkül is igazolható. A beírt kör sugarát r-el jelölve a terület: T = a*r/2+b*r/2+c*r/2 = r/2*(a+b+c). Mivel T = 6 és a+b+c = K = 12, 6 = r/2 * 12, amiből r = 1. Ezek után helyezzük el a háromszöget a (derékszögű) koordináta rendszerben úgy, hogy a derékszögnél levő csúcsot az origóra, a befogókat a két tengelyre fektetjük (az első síknegyedben). Ekkor a beírt kör középpontja a P(1;1) pont lesz. A megoldásban kapott értékekkel felírva a két adott ponton átmenő egyenes egyenletét láthatjuk, hogy P koordinátái kielégítik az egyenletet, azaz az egyenes valóban átmegy a P ponton.

Való igaz, gyakran jól jönne a sokkal hamarabbi megoldás. Főleg amikor (egy iskolában mondjuk) senki nem tudja megcsinálni. A hivatalos később már nem ér sokat.

Talán az lenne a legkézenfekvőbb megoldás, ha a feladatot beküldők beküldéskor egy checkbox-szerűvel hozzájárulnhatnának ahhoz hogy a beküldött megoldás pl a munkafüzetbe regisztrált tagok számára látható legyen. (azt hiszem ha nem nagyon ocsmány az e-KöMaL kódja akkor nem kell sokat kalapálni egy ilyen beépítéséhez rajta)

Akkor kimásolom neked a megoldásokat:

B.4647. Legyen a $\displaystyle 100$ egységkör halmaza $\displaystyle K$, továbbá a $\displaystyle K$ körei által lefedett $\displaystyle 101$-edik egységkör $\displaystyle k$.

Válasszuk ki $\displaystyle K$-ból azt a $\displaystyle c$ kört, amely lefedi $\displaystyle k$-nak a legalsó pontját; legyen $\displaystyle k$ és $\displaystyle c$ középpontja $\displaystyle O$ és $\displaystyle C$, $\displaystyle k$ legalsó pontja $\displaystyle B$, $\displaystyle c$ legfelső pontja $\displaystyle A$. Mivel $\displaystyle BO=CA=1$ függőleges szakaszok, így $\displaystyle AOBC$ paralelogramma, amiből $\displaystyle OA=CB$. Mivel viszont $\displaystyle c$ lefedi $\displaystyle B$-t, így $\displaystyle CB\le 1$, ahonnan $\displaystyle OA\le 1$, ami ekvivalens azzal, hogy $\displaystyle k$ lefedje $\displaystyle A$ pontot.

Tegyük fel indirekt, hogy $\displaystyle K^*:=K\setminus\{c\}$ nem tartalmaz olyan kört, amely lefedi $\displaystyle A$ pontot. Ekkor a $\displaystyle K^*$-beli körök középpontjainak távolsága $\displaystyle A$-tól mind $\displaystyle 1$-nél nagyobb. Legyen e véges sok távolság közül a legkisebbik $\displaystyle d>1$, ekkor minden $\displaystyle K^*$-beli középpont legalább $\displaystyle d$ távol van $\displaystyle A$-tól, vagyis a $\displaystyle K^*$-beli körök minden pontja legalább $\displaystyle d-1$ messzire esik az $\displaystyle A$ ponttól.

Legyen $\displaystyle P$ a $\displaystyle k$ körnek legfelső pontja, és tekintsük az $\displaystyle AP$ szakaszt (ez a szakasz létezik, hisz $\displaystyle A\neq P$ mert $\displaystyle c\neq k$ feltétel volt). Mivel $\displaystyle A$ és $\displaystyle P$ is $\displaystyle k$ határán vagy belsejében van, ezért a kör konvexitása miatt $\displaystyle AP$ szakasz $\displaystyle k$ belsejébe esik. Mi több, a $\displaystyle P$ pont magasabban helyezkedik, mint $\displaystyle A$, mert $\displaystyle O$ magasabban van $\displaystyle C$-nél, tudniillik $\displaystyle BC\le 1$ miatt $\displaystyle C\neq O$ a $\displaystyle B$ középpontú egységkörlapra esik, amely körlap legfelső pontja $\displaystyle O$. Tehát $\displaystyle A$ kivételével az $\displaystyle AP$ szakaszon lévő pontok mind $\displaystyle c$ felett találhatók, így $\displaystyle c$ nem tartalmazza őket.

Válasszunk az $\displaystyle AP$ szakaszon egy olyan $\displaystyle X$ pontot, amelyre $\displaystyle 0<AX<d-1$. Ekkor az $\displaystyle X$ pontot $\displaystyle c$ körlap nem tartalmazza, továbbá mivel feltevésünk szerint a $\displaystyle K^*$-beli körök minden pontja legalább $\displaystyle d-1$ messze van $\displaystyle A$-tól, így azok sem fedik le $\displaystyle X$ pontot. Vagyis $\displaystyle X$ olyan pont $\displaystyle k$ belsejében, amit egyik $\displaystyle K$-beli kör sem fed le, ez ellentmond a feltételnek.

Tehát van olyan $\displaystyle K^*$-beli kör, amely tartalmazza $\displaystyle c$ legfelső $\displaystyle A$ pontját. Ez bizonyítja a feladat állítását.

B.4549. Tegyük fel, hogy $\displaystyle f_1$, $\displaystyle f_2$ és $\displaystyle f_3$ egyenesek párhuzamosak, úgy helyezkednek el, hogy $\displaystyle f_2$ esik az $\displaystyle f_1$ és $\displaystyle f_3$ egyenesek közé, és elmetszik az $\displaystyle e_1,e_2,\dots,e_n$ egyenesek mindegyikét. Legyen $\displaystyle f_1$, $\displaystyle f_2$, $\displaystyle f_3$ és $\displaystyle e_i$ metszéspontja rendre $\displaystyle A_i$, $\displaystyle B_i$, $\displaystyle C_i$ minden $\displaystyle 1\le i\le n$-re, és a megfelelő pontokba egy tetszőleges $\displaystyle O$ origóból mutató helyvektorok $\displaystyle \vec{a_i}$, $\displaystyle \vec{b_i}$ és $\displaystyle \vec{c_i}$.

Legyen továbbá $\displaystyle \lambda:=\frac{d(f_3,f_1)}{d(f_2,f_1)}$. A párhuzamos szelők tétele szerint ekkor $\displaystyle \frac{A_iC_i}{A_iB_i}=\lambda$ (bármely $\displaystyle i=1,\dots,n$-re). Mivel pedig $\displaystyle A_i,B_i,C_i$ kollineáris és $\displaystyle B_i$ az $\displaystyle A_iC_i$ szakaszra esik, hisz $\displaystyle f_2$ van $\displaystyle f_1$ és $\displaystyle f_3$ között, így ezt úgy is írhatjuk, hogy $\displaystyle \vec{A_iC_i}=\lambda\cdot \vec{A_iB_i}$, azaz $\displaystyle \vec{c_i}-\vec{a_i}=\lambda\left(\vec{b_i}-\vec{a_i}\right)$. $\displaystyle (*)$

Jelölje az $\displaystyle A_1,\dots,A_n$ pontok $\displaystyle S_A$, a $\displaystyle B_1,\dots,B_n$ pontok $\displaystyle S_B$, illetve a $\displaystyle C_1,\dots,C_n$ pontok $\displaystyle S_C$ súlypontjába mutató helyvektort rendre $\displaystyle \vec{s_a}$, $\displaystyle \vec{s_b}$, $\displaystyle \vec{s_c}$. Ekkor $\displaystyle (*)$ értelmében, és persze felhasználva a súlypont definícióját, felírhatjuk a következőt:

$\displaystyle \vec{S_AS_C}=\vec{s_c}-\vec{s_a}=\frac1n\sum_{i=1}^n \vec{c_i}-\frac1n\sum_{i=1}^n \vec{a_i}=\frac1n\sum_{i=1}^n \left(\vec{c_i}-\vec{a_i}\right)=$

$\displaystyle =\frac1n\sum_{i=1}^n \lambda\left(\vec{b_i}-\vec{a_i}\right)=\lambda\cdot \left(\frac1n\sum_{i=1}^n \vec{b_i}-\frac1n\sum_{i=1}^n \vec{a_i}\right)=\lambda\cdot \left(\vec{s_b}-\vec{s_a}\right)=\lambda\cdot\vec{S_AS_B},$

amiből tüstént leolvasható, hogy az $\displaystyle S_C$ pont az $\displaystyle S_AS_B$ egyenesre esik.

A feladat megoldásához azt kell belátnunk, hogy az összes $\displaystyle S_\alpha$ pont egy egyenesre esik. Ehhez persze elegendő belátni, hogy bármely három $\displaystyle S_\alpha$ pont egy egyenesen van, hisz akkor minden $\displaystyle S_\alpha$ pont illeszkedik valamely két $\displaystyle S_\alpha$ pont által meghatározott egyenesre. Utóbbi tényt azonban a fenti okfejtéssel bebizonyítottuk, így készen is vagyunk.

Köszönöm, de főleg utóbbi nem sokat segített. Arra, hogy vektorok kellenének meg hogy ki kéne használni a párhuzamosságot, eddig is gondoltam. Csak hozzá sem tudok kezdeni. Nem lenne baj, ha a 6 pontos feladatok megoldása aránylag hamar megjelenne online.

B.4647. Van 100 egységkörünk, ezek halmaza legyen $\displaystyle K$, és még van egy 101., amit együttesen lefednek, ez legyen $\displaystyle k$.

Mi garantálná azt, hogy legyen olyan $\displaystyle c\in K$ kör, amelynek a legfelső pontja le van fedve $\displaystyle K$ többi köre által? Legegyszerűbben úgy lehetne ezt elérni, hogyha $\displaystyle c$ legfelső pontja netán $\displaystyle k$-ba esne, hisz már van olyan feltételünk, hogy $\displaystyle k$-t lefedik $\displaystyle K$ körei.

A megoldáshoz szerintem elég lesz a következő két kulcslépést belátnod:

1. állítás: $\displaystyle k$ pontosan akkor tartalmazza $\displaystyle c$ legfelső pontját, hogyha $\displaystyle c$ lefedi $\displaystyle k$ legalsó pontját.

2. állítás: legyen $\displaystyle k$ legfelső pontja $\displaystyle P$, és $\displaystyle c$ legfelső pontja $\displaystyle A$. Ekkor $\displaystyle AP$ szakasz belső pontjait $\displaystyle k$ lefedi, de $\displaystyle c$ nem.

B.4649. Vektorok és a párhuzamos szelők tétele segítségével bizonyítsd be, hogy az említett súlypontok közül bármely három egy egyenesre esik.

Valaki tudna mondani egy szép megoldást a B4647 és B4649 feladatokra? Előre is kösz.

A622. potya feladat volt (hivatalos megoldás is fent van.)

$\displaystyle 7^{7*h}+1=(7^h+1)*L*M$, ahol

$\displaystyle L=T^3-B, M=T^3+B, T=7^h+1, B=7^k*(T^2-7^h), h=2k-1$

Így már $\displaystyle \frac {7^{7*h}+1}{7^h+1}$ is összetett, ha $\displaystyle h$ páratlan szám. Egyébként Aurifeuillean faktorizáció a neve. Aki ezt ismeri az kb. 1 perc alatt meg is oldotta. Más alapokra, kitevőkre is van hasonló faktorizáció, ez mind ismert, és valószínűtlen, hogy lenne más felbontás is.

Ami nekem szintetikus úton kijött az A.614. feladatból a következő, önmagában is érdekes feladat.

Legyen $\displaystyle ABC$ háromszög $\displaystyle BC$ oldalához írt köre $\displaystyle h$, amely a $\displaystyle BC$ oldalt $\displaystyle D$-ben érinti. Tekintsük azt a $\displaystyle k$ kört, amely áthalad a $\displaystyle B$ és $\displaystyle C$ pontokon, és érinti $\displaystyle h$-t (de nem a $\displaystyle BC$ egyenes). Mutassuk meg, hogy $\displaystyle h$ és $\displaystyle k$ érintési pontját $\displaystyle P$-vel jelölve, $\displaystyle PD$ egyenes felezi a $\displaystyle BPC$ szöget.

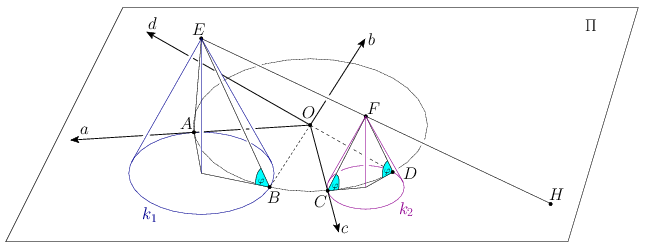
Ha hasonlóság, akkor Monge-kúpok.

Legyen $\displaystyle O,A,B,C,D$ ugyanaz, mint a te megoldásodban. Rajzoljuk meg a $\displaystyle \Pi$ síkban azt a két irányított kört ($\displaystyle k_1$ és $\displaystyle k_2$), ami az $\displaystyle A,B,C,D$ pontokban érinti az $\displaystyle a$ és a $\displaystyle b$, illetve a $\displaystyle c$ és a $\displaystyle d$ egyenest. A két körre illesszünk egy-egy kúpot, amelyek alkotói a $\displaystyle \Pi$ síkkal $\displaystyle \varphi$ szöget zárnak be. Ezek csúcsai legyenek $\displaystyle E$, illetve $\displaystyle F$. Legyen $\displaystyle H$ a két kúp hasonlósági pontja, ami az $\displaystyle EF$ egyenes és $\displaystyle \Pi$ döféspontja.

Ha az irányításokat megfelelően választjuk, akkor $\displaystyle E\in A_\varphi \cap B_\varphi$ és $\displaystyle F\in \Gamma_\varphi \cap \Delta_\varphi$, így $\displaystyle H\in EF\subset \Sigma_\varphi$.

Mivel $\displaystyle O$ triviálisan a $\displaystyle \Sigma_\varphi$ síkban van, $\displaystyle OH$ közös egyenese az összes $\displaystyle \Sigma_\varphi$ síknak.

(Az A. 529. feladat ugyanez, csak hiperbolikusban.)

"Hasonlóan adódik a $\displaystyle \Gamma_\varphi$ és $\displaystyle \Delta_\varphi$ síkok metszésvonala, ami a következő pontokból áll:" résznél a képlet helyesen:

$\displaystyle \left((\gamma-\delta)x,(\gamma D-\delta C)x,(C-D)\tg\varphi\cdot x\right).$

Bár ez annyira nem zavaró.

A megoldásod érdekes, de szerintem annyira nem triviális. Mondjuk én nyilván miután sikertelenül megpróbáltam megjeleníteni az ábrát, koordinátáztam. Nagyon jó gyakorlópélda koordinátákra, olcsón, kb. egy órán belül kijött (+későbbi pontosítgatások).

Egyébként ha már itt tartunk, szerintem az A.617 feladat ennél még olcsóbb volt, bár a statisztika ezzel nem ért egyet. :) A megoldás(oka)t inkább még nem lőném le.

Leírok akkor egy erős vázlatot az A619-re:

Először felveszünk egy térbeli koordinátarendszert, az $\displaystyle O$ origó természetesen a félegyenesek közös kiindulópontja, a $\displaystyle z=0$ sík pedig $\displaystyle \Pi$. lesz. Az $\displaystyle a$ egyenesének egyenlete $\displaystyle y=Ax$, $\displaystyle z=0$, a többié hasonló. A koordinátarendszer megválasztható úgy, hogy $\displaystyle |A|\neq |B|$ és $\displaystyle |C|\neq |D|$ legyen (illetve pl. $\displaystyle A=B$ esetben $\displaystyle \Sigma$ triviálisan illeszkedik $\displaystyle a$-ra és $\displaystyle b$-re, kész).

$\displaystyle A_\varphi$ egyeletének meghatározása: tudjuk, hogy ez a sík rajta van az $\displaystyle y=Ax$, $\displaystyle z=0$ egyenesen; most keresünk egy harmadik pontot, ami rá illeszkedik.

Vegyük az $\displaystyle y=-\frac1A x$, $\displaystyle z=0$ egyenest (ez merőleges $\displaystyle a$-ra), ez az egyenes $\displaystyle \varphi$ szöget zár be $\displaystyle A_\varphi$-vel. Keressük akkor meg az $\displaystyle A_\varphi$ síkon azt a $\displaystyle Q$ pontot, aminek merőleges vetükete $\displaystyle \Pi$-re a $\displaystyle P\left(1,-\frac1A,0\right)$ pont lesz. Mivel $\displaystyle OPQ$ háromszög derékszögű és $\displaystyle O$-nál $\displaystyle \varphi$ szög van, így könnyen látható, hogy $\displaystyle Q$ koordinátái:

$\displaystyle \left(1,-\frac1A,\epsilon_a\tg\varphi\sqrt{1+\frac1{A^2}}\right),$

ahol $\displaystyle \epsilon_a$ egy olyan előjel, ami kizárólag az $\displaystyle a$ félegyenes irányától (a forgatás irányától) függ.

Ha most az $\displaystyle A_\varphi$ síkot a $\displaystyle (0,0,0)$, $\displaystyle (1,A,0)$, $\displaystyle Q$ pontokra illesztjük, a kapott egyenletrendszer megoldásával $\displaystyle A_\varphi$ egyenlete

$\displaystyle -Ax+y+\frac{\alpha}{\tg \varphi} z=0$

lesz, ahol $\displaystyle \alpha=\epsilon_a\sqrt{A^2+1}$ egy $\displaystyle \varphi$-től független konstans.

Ha most $\displaystyle A_\varphi$ és $\displaystyle B_\varphi$ metszésvonalát kiszámoljuk ($\displaystyle B_\varphi$ egyenlete $\displaystyle -Bx+y+\frac{\beta}{\tg\varphi}$), a következő pontok mértani helye adódik:

$\displaystyle \left((\alpha-\beta)x,(\alpha B-\beta A)x,(A-B)\tg\varphi\cdot x\right)\quad\forall x\in R$

Egyébként $\displaystyle \alpha\neq \beta$ mert feltettük, hogy $\displaystyle |A|\neq |B|$, szóval ez itt rendben van.

Hasonlóan adódik a $\displaystyle \Gamma_\varphi$ és $\displaystyle \Delta_\varphi$ síkok metszésvonala, ami a következő pontokból áll:

$\displaystyle \left((\alpha-\beta)x,(\alpha B-\beta A)x,(A-B)\tg\varphi\cdot x\right).$

Na most pedig legyen $\displaystyle \Sigma$ egyenlete $\displaystyle S(x,y,z)=\sigma_1 x+\sigma_2 y+\sigma_3 z$. Ebből csak az érdekel minket, hogy $\displaystyle S(x,y,z)$ additív függvény, vagyis ha teljesül rá, hogy

$\displaystyle \left\{\matrix{S((\alpha-\beta)x,(\alpha B-\beta A)x,(A-B)\tg\varphi\cdot x)=0\cr S((\gamma-\delta)x,(\gamma D-\delta C)x,(C-D)\tg\varphi\cdot x)=0}\right.$

abból következik, hogy

$\displaystyle 0=(C-D)\cdot S((\alpha-\beta)x,(\alpha B-\beta A)x,(A-B)\tg\varphi\cdot x)-$

$\displaystyle -(A-B)\cdot S((\gamma-\delta)x,(\gamma D-\delta C)x,(C-D)\tg\varphi\cdot x)=$

$\displaystyle =S\left(K x,L y,0\right),$

ahol $\displaystyle K=(C-D)(\alpha-\beta)-(A-B)(\gamma-\delta)$ és $\displaystyle L=(\alpha B-\beta A)(C-D)-(\gamma D-\delta C)(A-B)$ $\displaystyle \varphi$-től független konstansok.

A $\displaystyle (Kx,Ly,0)$ pontok egy egyenest határoznak meg, ezen az egyenesen tehát minden $\displaystyle \Sigma_\varphi$ sík áthalad.

Kivételt képez persze, amikor $\displaystyle K=L=0$; ebból következik, hogy $\displaystyle A_\varphi\cap B_\varphi$ és $\displaystyle \Gamma_\varphi\cap \Delta_\varphi$ pontjaiba mutató helyvektorok lineárisan függőek, avagy a két egyenes minden $\displaystyle \varphi$-re egybeesik. Most lehetünk lusták, és egyfelől mondhatjuk erre azt, hogy ilyenkor $\displaystyle \Sigma_\varphi$ nem létezik, így a feladat kitűzése által nem megengedett helyzetben vagyunk ("az a[z egyértelmű] sík, ami..."), vagy mondhatjuk azt, hogy $\displaystyle \Sigma_\varphi$-t akkor tetszőleges, a közös metszésvonalra illeszkedő síknak/határhelyzetként értelmezzük; akkor meg igaz rá a feladat állítása.

-------------

Tegyük fel, hogy a $\displaystyle \varphi$-hez tartozó $\displaystyle A$, $\displaystyle B$, $\displaystyle \Gamma$, $\displaystyle \Delta$ síkok átmennek egy közös $\displaystyle e$ egyenesen. Vegyük $\displaystyle e$-nek valamely $\displaystyle O$-tól különböző $\displaystyle X$ pontját. Ha $\displaystyle X$-ből merőlegest állítunk mondjuk $\displaystyle a$-ra, akkor a kapott merőleges egyenes $\displaystyle \varphi$ szöget zár be $\displaystyle \Pi$-vel. Az olyan pontok mértani helye $\displaystyle \Pi$-n, melyeket $\displaystyle X$-szel összekötve, $\displaystyle \Pi$-vel $\displaystyle \varphi$ szöget bezáró egyenest kapunk, az nyilvánvalóan egy $\displaystyle k$ kör, és az $\displaystyle X$-szel összekötő egyenesek egy kúpot határoznak meg. Most ha $\displaystyle a$ egyenesét vissza akarjuk keresni, akkor a Pitagorasz-tétel és megfordítása szerint $\displaystyle a\cap k$ fix távolságra van $\displaystyle O$-tól, így legfeljebb kétféle egyenes merülhet fel, mint $\displaystyle a,b,c,d$ egyenese.

Ha $\displaystyle a,b,c,d$ közül valamely kettő ugyanazon az egyenesen van, de ellentétes irányú, akkor $\displaystyle e$ egyenes egyben $\displaystyle a$ és $\displaystyle b$ egyenese kell legyen, vagyis a $\displaystyle \Pi$ síkon van. Ilyenkor tehát $\displaystyle a,b,c,d$ is az $\displaystyle e$-re illeszkedik. A másik lehetőség, hogy $\displaystyle a,b,c,d$ max. kétféle félegyenest tartalmaznak. Mindkét eset teljesen degenerált, ezekre viszont $\displaystyle \Sigma$ nem értelmezhető.

Azt szoktak mondani, hogy gombon nincs hasonlosag. Ugy latszik, hasonlosaggal analog jelensegek viszont akadhatnak.

A vegere, ugy latszik, elfogyott a lendulet, az A. 619. amilyen konnyu, olyan kevesen oldottak meg. Az enyem 2 pontert:

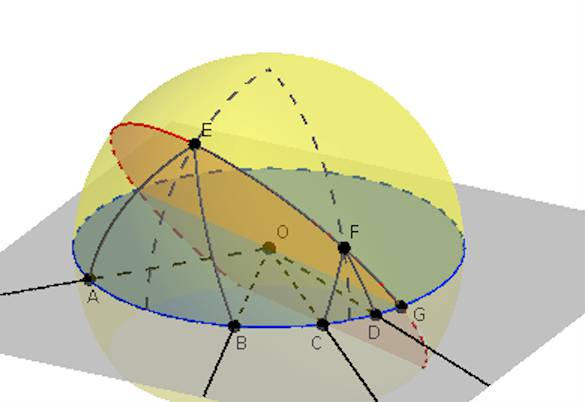
A. 619. Adott a térben négy, egy pontból induló félegyenes, a, b, c és d, amelyek a $\displaystyle \Pi$ síkban fekszenek. Tetszőleges $\displaystyle \varphi$ hegyesszögre forgassuk el $\displaystyle \Pi$-t a négy félegyenes körül pozitív irányban $\displaystyle \varphi$-vel; az így kapott síkokat jelölje rendre A$\displaystyle \varphi$, B$\displaystyle \varphi$, C$\displaystyle \varphi$, illetve D$\displaystyle \varphi$. Legyen S$\displaystyle \varphi$ az a sík, ami illeszkedik az A$\displaystyle \varphi$ és a B$\displaystyle \varphi$ síkok metszésvonalára, valamint a C$\displaystyle \varphi$ és a D$\displaystyle \varphi$ metszésvonalára is. Mutassuk meg, hogy a különböző $\displaystyle \varphi$ szögekhez tartozó S$\displaystyle \varphi$ síkok egy közös egyenesre illeszkednek.

1: rakjunk egy egysegsugaru gombot a kozos tartopontra, a gombbol a felegyenesek altal kimetszett pontok A,B,C,D

2: az (A,B) pontpar egyik pontjat csereljuk fel a gomb ellentetes pontjaval, a (C,D) egyik tagjaval is jarjunk el ugyanigy.

3: vegyunk fel egy $\displaystyle \varphi$ szoget, a sikparok metszesvonalai messek a gombot E es F pontokban.

4: Legyen (a kisebb) AB iv felezopontja $\displaystyle M_E$, CD ive $\displaystyle M_F$. Az EF fokor messe az alapsikot G-ben.

5: Szimmetria miatt az $\displaystyle E M_E$ es $\displaystyle F M_F$ fokorok merolegesek az alapsikra

6: felcsapjuk a wikipediat, es leolvassuk, hogy a,b,c, A,B,90 parameteru derekszogu haromszogek eseten

$\displaystyle tan~a=tan~A \cdot sin~b$

fennall (R4)

7:

$\displaystyle tan EM_E = tan EBM_E \cdot sin M_EB = tan EGM_E \cdot sin M_EG$

$\displaystyle tan FM_F = tan FDM_F \cdot sin M_FD = tan FGM_F \cdot sin M_FG$

8: $\displaystyle EBM_E=\varphi=FDM_F$, igy a G pontra

$\displaystyle c=\frac{sin M_EB}{sin M_EG}=\frac{sin M_FD}{sin M_FG}$

9: Mas $\displaystyle \varphi$ szogek eseten

$\displaystyle EGM_E< = arctan(c \cdot tan(\varphi)) = FGM_F<$

10: A G pontbol EG es FG minden $\displaystyle \varphi$ eseten ugyanakkora szoget zar be az alappal.

11: Innen valahogy kiszedjuk, hogy EFG egy egyenesen vannak, belatunk valami folytonossag szerut peldaul.

Szerintem ezt a hugom is megcsinalta volna egy csokiert se otlet, se szamolas, se semmi nem kell bele. Gomb felvetele nelkul is meg lehet csinalni, persze: http://wildegg.com/papers/ProjectiveTrig.pdf

Ez szép, köszönöm!

A Fálesz Mihály által [900]-ban leírt egyenlőtlenséget bizonyítjuk, ebből c=1 esetén következik A616.

Mivel x+y+z=0, ezért x,y,z közt van kettő olyan, melyek szorzata nemnegatív. Tegyük fel, hogy $\displaystyle xy\geq0$. (1)-et átrendezve és felhasználva, hogy z=-x-y

$\displaystyle \left(\frac{4ac}{(a+c)^2}\right)^{x^2}\left(\frac{2(a+b)c}{(a+c)(b+c)}\right)^{2xy}\left(\frac{4bc}{(b+c)^2}\right)^{y^2}\leq1$

Ha x+y=0, akkor nyilván teljesül az egyenlőtlenség, ellenkező esetben a fentivel ekvivalens

$\displaystyle \left(\frac{4ac}{(a+c)^2}\right)^{\frac{x^2}{(x+y)^2}}\left(\frac{2(a+b)c}{(a+c)(b+c)}\right)^{\frac{2xy}{(x+y)^2}}\left(\frac{4bc}{(b+c)^2}\right)^{\frac{y^2}{(x+y)^2}}\leq1$

A bal oldalra alkalmazva a súlyozott számtani és mértani közép közti összefüggést, elég belátnunk, hogy

$\displaystyle \frac{4ac}{(a+c)^2}\frac{x^2}{(x+y)^2}+\frac{2(a+b)c}{(a+c)(b+c)}\frac{2xy}{(x+y)^2}+\frac{4bc}{(b+c)^2}\frac{y^2}{(x+y)^2}\leq1$

$\displaystyle \frac{(c-a)^2}{(a+c)^2}x^2+\frac{(c-a)(c-b)}{(a+c)(b+c)}2xy+\frac{(c-b)^2}{(b+c)^2}y^2\geq0$

Ez pedig nyilvánvaló, mert a bal oldal teljes négyzet

Kérlek leírnád?

Köszönöm, így már rendben az elemibb bizonyítás

Kedves Péter,

A feladatnak van egy szimmetrikus változata: Ha $\displaystyle a,b,c>0$ és $\displaystyle x+y+z=0$, akkor

$\displaystyle a^{x^2} b^{y^2} c^{z^2} \left(\frac{a+b}2\right)^{2xy} \left(\frac{a+c}2\right)^{2xz} \left(\frac{b+c}2\right)^{2yz} \le 1.$

Ha tehát van egy elemi megoldásod az $\displaystyle x,y\ge0$ esetre, akkor az megoldja a többi esetet is.

Az A616-ra nem érkezett jó megoldás és még nincs fenn a hivatalos verzió. Itt egy megoldásvázlat, hibája, hogy kicsit "durva", nem középiskolás anyagot használ. Érdekelne egy elemibb megoldás, mely például a súlyozott számtani és mértani közép közti egyenlőtlenséget használja. Ebben eljutottam valameddig, de az xy<0, (1-a)(1-b)>0 esetben elakadtam.

$\displaystyle \left(\frac{1+a}2\right)^{2x(x+y)}\left(\frac{1+b}2\right)^{2y(x+y)}\geq a^{x^2}b^{y^2}\left(\frac{a+b}2\right)^{2xy}$,   a,b >0 és x,y tetszőleges valós számok

A bizonyításban az alábbi ismert analízis fogalmakat fogjuk felhasználni:

1. Ha p és q pozitív valós számok, akkor

2. Schwarz egyenlőtlenség. Ha f és g az [a,b] intervallumon négyzetesen integrálható függvények, akkor

Az eredeti egyenlőtlenség a=1 vagy b=1 esetén könnyen láthatóan teljesül, ezért a továbbiakban feltesszük, hogy $\displaystyle a,b ~\neq1$. Véve az egyenlőtlenség mindkét oldalának természetes alapú logaritmusát, majd átrendezve, az eredetivel ekvivalens

Mivel

$\displaystyle \ln{\frac{(1+a)^2}{4a}}>0$ és $\displaystyle \ln{\frac{(1+b)^2}{4b}}>0$, ezért (3) bizonyításához elég belátni, hogy a diszkriminánsa nempozitív, azaz

Tetszőleges p>1 számra

$\displaystyle \ln{p}=\int_1^p\frac{dx}x=\int_0^1\frac{p-1}{(p-1)x+1}dx=\int_0^1\frac{dx}{x+\frac1{p-1}}$

ezért felhasználva a (2)-t

$\displaystyle \ln{\frac{(1+a)^2}{4a}}\ln{\frac{(1+b)^2}{4b}}=\int_0^1\frac{dx}{x+\frac{4a}{(a-1)^2}}\int_0^1\frac{dx}{x+\frac{4b}{(b-1)^2}}\geq\left(\int_0^1\frac{dx}{\sqrt{\left(x+\frac{4a}{(a-1)^2}\right)\left(x+\frac{4b}{(b-1)^2}\right)}}\right)^2$

A számolást nem részletezve, felhasználva (1)-et kapjuk

$\displaystyle \ln{\frac{(1+a)^2}{4a}}\ln{\frac{(1+b)^2}{4b}}\geq\left(2\ln{\frac{(1+a)|b-1|+(1+b)|a-1|}{2\sqrt a|b-1|+2\sqrt b|a-1|}}\right)^2$

De

$\displaystyle \frac{(1+a)|b-1|+(1+b)|a-1|}{2\sqrt a|b-1|+2\sqrt b|a-1|}=\left\{\matrix{\frac{1+\sqrt{ab}}{\sqrt a+\sqrt b} & ha & (a-1)(b-1)>0 \cr \frac{\sqrt a+\sqrt b}{1+\sqrt{ab}} & ha & (a-1)(b-1)<0}\right.$

Tehát

Most már csak az kell észrevenni, hogy tetszőleges $\displaystyle p\geq q>0$ és $\displaystyle 0<x\leq y$ valós számokra

(5) és (6) valamint $\displaystyle 2\sqrt{ab}\leq a+b$ alapján azonnal adódik (4).

A bizonyítás alapján látszik, hogy egyenlőség az alábbi esetekben van:

1. x=0 b=1 , a és y tetszőleges

2. y=0 a=1 , b és x tetszőleges

3. a=b=1, x és y tetszőleges

4. $\displaystyle a=b\neq1$ és x+y=0

Nagyon jó kérdés! Gondolkozom rajta.

Ez haromszogre hogy nezne ki? Hol eles a hatar? Beirt kor atmerojenel kevesebbel nem lehet, legkisebb magassagvonal hosszara van konstrukciom. (ahol a sav euklideszi szelesseget ertjuk)