| [288] HoA | 2007-01-23 21:56:03 |
 Van valakinek A. 413. -ra olyan megoldása, amiből kiderül, miért A-jelű ?
|
|
| [287] Lacczyka | 2007-01-16 21:35:05 |
 Nos, ha már ilyen szépen engedélyt kaptam, akkor meg is írnék egy megoldást: a B. 3953.-as feladatra.
Legyenek a számok a1;a2;a3;...a100; Ha a1=a2=...=a99=(-1), és a100=99, akkor pontosan 99 nemnegatív összegű pár van. Most bizonyítjuk, hogy ennyi mindig van:
Fogjuk a 100 számot, és párokat alkotunk belőlük úgy, hogy minden egyes számot egyszer használunk. Ezen párok összege nyilván megegyezik a 100 szám összegével, pl:
(a1+a2)+(a3+a4)+...+(a99+a100)=0
Elmondhatjuk, hogy ezek közül a párok közül legalább az egyik nemnegatív, mivel ha mind negatív lenne, akkor az összes összege negatív lenne.
Ha sikerültne 99 ilyen összeget alkotni úgy, hogy minden sorban pont a 100 szám összege szerepeljen, és egy adott pár ne szerepeljen 2 összegben, akkor készen lennénk, mert minden összegben találunk nemnegtív párt, és ezek mind különbözők.
Ezen a ponton szeretném felhívni a figyelmet a KöMaL decemberi számának első cikkére: Kiss György: Hogyan szervezzünk körmérkőzéses focibajnokságot? Ha az ember belegondol, akkor a probléma egy és ugyanaz: focibajnokságnál is azt várjuk el, hogy minden fordulóban játszon az összes csapat, és hogy két csapat egy őszi szezon alatt csak egyszer játszon egymással.
Még ha nem is tudnánk, hogy focibajnokság szervezhető, akkor is bőséges felvilágosítással szolgál az előbb említett cikk. 100 csapat részvételével egy bajnokságban pont 99 fordulóra lenne szükség, vagyis készen vagyunk a feladat megoldásával. Nem azt mondom, hogy ez a legjobb módja a feladat megoldásának, de szerintem figyelemre méltó.
Üdv Mindenkinek: Lacczyka
|
|
|
| [285] Lacczyka | 2007-01-15 20:00:00 |
 Üdv!
Lévén új a fórumon, szeretném megkérdezni, hogy mikor számít a határidő lejártnak? Mert ugyebár elvileg 15.-ével lejár a határidő, de én is küldtem már be feladatokat egy-két nap késéssel, és minden további nélkül elfogadták. Mikortól etikus a feladatokról írni a fórumba?
Lacczyka
|
|
| [284] Sümegi Károly | 2007-01-04 19:35:22 |
 A képlet még egyszer, mert nem sikerült: sin5A*cosA+sinA*cos5A. A végeredményt még valamivel szorozni kell(32), elnézést kérek, hogy csak a piszkozataimat találtam meg, de nagy vonalakban ez volt a megoldásom.
|
| Előzmény: [283] Sümegi Károly, 2007-01-04 19:21:44 |
|
| [283] Sümegi Károly | 2007-01-04 19:21:44 |
 B. 3948.-hoz szerintem nagyon-nagyon szépen eljuthatunk, ha először osztunk 4-gyel, majd a/2=sinA és b=cosA helyettesítést elvégezzük. A vizsgálandó kifejezés 2-szeresére sinAxcos5a+sin5AxcosA=sin6A képletet kapjuk. Innen a keresett összeg [-1/2,1/2] intervallumban lesz és nagyon sok helyen felveszi a szélsőértékeket, de mind meghatározható! Szerintem szépség-díjas:)
|
| Előzmény: [272] S.Ákos, 2006-12-28 19:39:52 |
|
| [282] jenei.attila | 2007-01-02 19:13:32 |
 Szép. Először én is így próbálkoztam, aztán eszembe jutott az inverzió, és úgy gyorsabban el tudtam intézni. Egyébként az én megoldásomban az EG egyenes inverz képére nincs is szükség, mert ha már tudjuk, hogy az F a P inverz pontja és az AA" inverz képe átmegy P, már következik, hogy AA" átmegy F-en. Szerintem mindkét megoldás tanulságos, egész jó kis feladat volt.
|
| Előzmény: [281] HoA, 2007-01-02 17:18:42 |
|
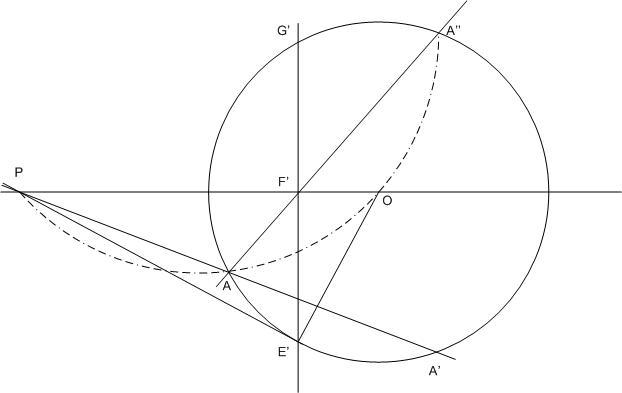
| [281] HoA | 2007-01-02 17:18:42 |
 Inverzió nélküli bizonyítás: [280] szerint P, A, O, A'' egy körön van. Legyen PO és AA'' metszéspontja F' . Ekkor PF' * F'O = AF' * F'A'' . A PO-ra F' -ben emelt merőleges és az eredeti kör metszéspontjai legyenek E' és G' . Így AF' * F'A'' = F'E' * F'G' = F'E'2 . A két egyenlőségből PF' * F'O = F'E'2 ,  , PF'E' és E'F'O derékszögű , PF'E' és E'F'O derékszögű  -ek hasonlók, PE'O -ek hasonlók, PE'O  E'-nél derékszögű, tehát E' = E és így F' = F, vagyis A, F és A" egy egyenesen van. E'-nél derékszögű, tehát E' = E és így F' = F, vagyis A, F és A" egy egyenesen van.
|
 |
| Előzmény: [280] jenei.attila, 2007-01-01 19:02:59 |
|
| [280] jenei.attila | 2007-01-01 19:02:59 |
 Jelöljünk ki a körön egy A pontot, és kössük össze P-vel. AP egyenes és a kör másik metszéspontja legyen A'. Nyilván igaz, hogy AP*A'P=h*h. B legyen a kör egy másik pontja. AP*BP=h*h csak akkor, ha BP=A'P, amiből B=A' (AB egyenes átmegy P-n), vagy B=A", ahol A" az A' OP egyenesre való tükörképe. Ez utóbbi esetben kell bizonyítani, hogy AA" átmegy F-en.
Vegyük észre, hogy az F pont a P pont körre vonatkozó inverze (vagyis OF*OP=r*r az OEP derékszögű háromszögre vonatkozó befogótétel szerint, ahol E a P-ből húzott egyik érintő érintési pontja (G a másik érintő érintési pontja)). Bebizonyítjuk, hogy az AA" egyenes körre vonatkozó inverz képe az AOA"P kör, az EG egyenes inverz képe pedig az EOGP kör. Vagyis az egyeneseknek megfelelő inverz körök a P pontban metszik egymást, amiből következik, hogy az egyenesek a P inverz pontjában, F-ben metszik egymást.
A'OA" szög=2*POA" szög, mivel A" az A' OP-re való tükörképe. De PAA" szög=A'AA" szög a körünkben az A'A" ívhez tartozó kerületi szög. A'OA", pedig ugyanezen ívhez tartozó középponti szög. Ezért POA" szög=A'AA" szög=PAA" szög, amiből következik, hogy A, O, A", P pontok egy körön vannak. Ez a kör pedig éppen az AA" egyenes eredeti körre vonatkozó inverz képe. Az, hogy az EG egyenes inverz képe az EOGP kör, nagyon könnyen látható.
|
| Előzmény: [279] S.Ákos, 2006-12-31 21:14:52 |
|
| [279] S.Ákos | 2006-12-31 21:14:52 |
 vki felrakná a B.3947. bizonyítását?
|
|
|
| [277] Csimby | 2006-12-29 14:21:57 |
 A.411. Legyenek x1,x2,...,xn pozitív valós számok, amikre teljesül, hogy

Igazoljuk, hogy 
Legyen xk=x a legkisebb és xj=y a legnagyobb az xi-k közül, ekkor 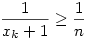 és és  vagyis x vagyis x n-1 n-1 y. Továbbá y. Továbbá  miatt x+y+2<xy+x+y+1 vagyis 1<xy. miatt x+y+2<xy+x+y+1 vagyis 1<xy.
x helyébe n-1-et, y helyébe 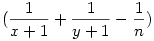 -et írva a feltétel továbbra is teljesül ( -et írva a feltétel továbbra is teljesül (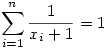 ). ).
Viszont  (biz. lentebb) miatt (biz. lentebb) miatt  értéke csökken. Ezt az eljárást folytatva A értékét minden lépésben csökkentjük egészen addig amíg minden i-re xi=n-1 nem lesz, amikor is a bizonyítandó állítás triviális. És így, mivel A-t mindig csökkentettük a kezdeti állítás is igaz volt. értéke csökken. Ezt az eljárást folytatva A értékét minden lépésben csökkentjük egészen addig amíg minden i-re xi=n-1 nem lesz, amikor is a bizonyítandó állítás triviális. És így, mivel A-t mindig csökkentettük a kezdeti állítás is igaz volt.
 átrendezés után: átrendezés után:
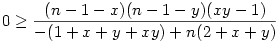
Ahol a számlálóban: n-1-x 0 ; n-1-y 0 ; n-1-y 0 ; xy-1>0 0 ; xy-1>0
A nevező pedig mindig pozitív hiszen: 1+x+y+xy 1+n-1+y+(n-1)y=n(y+1)<2n+nx+ny=n(y+1)+n(x+1) 1+n-1+y+(n-1)y=n(y+1)<2n+nx+ny=n(y+1)+n(x+1)
Így a tört értéke valóban mindig negatív.
Van valakinek más, esetleg közepes megoldása? Vagy lát valaki hibát az enyémben?
|
|
|
|
| [274] jenei.attila | 2006-12-28 20:21:41 |
 Hát szerintem is csak a maximumra adtam választ, de ha azt kérdezik milyen NAGY lehet a kifejezés értéke, akkor ez a maximumot jelenti, különben azt kérdezték volna, hogy pl. milyen határok közt változhat a kifejezés értéke. Egyébként ugyanaz a megoldásod, mint az enyém.
|
| Előzmény: [272] S.Ákos, 2006-12-28 19:39:52 |
|
| [273] S.Ákos | 2006-12-28 19:51:43 |
 B.3950.(vázlat)
Kijelölöd az első esetben az 1,2,4,8,16 elemeket. Bárhogy is választasz ki elemeket a többi szám közül, a kijelöltek halmazhoz vételével 1 féleképp el tudod érni, hogy megfelelő halmazt kapj, így 22001 jó részhalmaz van.
A második esetben a kijelöltek az 1,2,4,8 elemek. itt 22002 a jó részhalmazok száma.
|
| Előzmény: [271] jenei.attila, 2006-12-28 13:41:47 |
|
| [272] S.Ákos | 2006-12-28 19:39:52 |
 ezzel szerintem csak a maximumra adtál választ, de a feladat azt kérte, hogy milyen nagy lehet a kifejezés értéke, amihez szerintem a minimum meghatározása is hozzátartozik.
nagyon vázlatosan: Mivel a2+4b2=4, így fennáll
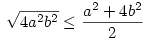
, vagyis
|ab| 1 1
, így a függvényt csak a [-1;1] intervallumon kell vizsgálni. A keresett szélsőértékeket a helyi maximum és minimum értékek illetve az intervallum két határánál lehetséges(a minimum 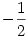 , a maximum , a maximum 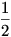 ) Az ezeknél felvett értékek 16;-16;16;-16. így a minimum -16, a maximum 16. példaszámpárok: ) Az ezeknél felvett értékek 16;-16;16;-16. így a minimum -16, a maximum 16. példaszámpárok: 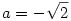  és és 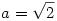 
a függvényhez például így is el lehetett jutni:
3a5b-40a3b3+48ab5=ab(3a4-40a2b2+48b4)=ab(3a4+24a2b2+48b4-24a2b2-40a2b2)=ab(3(a4+8a2b2+16b4)-64a2b2)=
=ab(3(a2+4b2)2-64a2b2)=ab(3*42-64a2b2)=ab(3*16-4*16a2b2)=16ab(3-4a2b2)
|
| Előzmény: [271] jenei.attila, 2006-12-28 13:41:47 |
|
| [271] jenei.attila | 2006-12-28 13:41:47 |
 Csak hogy életben tartsam a topikot, a B.3948-hoz is írok egy megoldást (a B.3950 megoldása tényleg érdekelne, én elég sokat vacakoltam vele).
Az egyszerűség kedvéért m-mel fogom jelölni a maximalizálandó kifejezést. m=ab(3a4-40a2b2+48b4). Az a2+4b2=4 feltételből mindkét oldalhoz 4ab-t adva, kapjuk hogy ab>=-1. A feltételt négyzetre emelve: a4+16b4=16-8a2b2. Ezért m=ab(3(16-8a2b2)-40a2b2)=16ab(3-4a2b2). Bevezetve az x=ab jelölést, a 3x-4x3 polinom maximumát keressük a [-1,+végtelen)intervallumon. [-1,0] intervallumon lokális minimuma van, a maximumot -1-ben veszi fel, itt 1 az értéke. Nem negatív x-szel az 1/2, 1/2, x számokra alkalmazzuk a Sz-M közép egyenlőtlenséget:  . Ebből 1>=3ab-4a3b3. Vagyis m maximális értéke mindkét esetben 16. Ezt, a feltételt kielégítve, mindkét esetben fel is tudja venni: ab=-1 esetén pl. . Ebből 1>=3ab-4a3b3. Vagyis m maximális értéke mindkét esetben 16. Ezt, a feltételt kielégítve, mindkét esetben fel is tudja venni: ab=-1 esetén pl.  , ab=1/2 esetén , ab=1/2 esetén  . .
|
|
| [270] jenei.attila | 2006-12-25 21:16:59 |
 Először is boldog karácsonyt kívánok minden kedves fórumtársnak.
A B.3950 feladathoz írok egy megoldást, és kíváncsian várom másokét is.
Vezessünk be egy jelölést: Xnm jelntse az X halmaz azon részhalmazainak halmazát, amelyekben az elemek összege n-nel osztva m maradékot ad. Tehát a feladat szövege szerint D=|H327| és S=|H1614|. Biznyítandó, hogy S=2D. Definíció szerint legyen P:=H\{16} és Q:=H\{16,8}=P\{8}. Három állítást bizonyítunk be, amelyből következik az S=2D állítás:
1. S=|H1614|=2|P1614| Ez azért igaz, mert ha egy H1614-beli kiválasztásból elhagyjuk az esetlegesen benne szereplő 16-os számot, egy P1614-beli kiválasztást kapunk, ha pedig nem szerepelt benne a 16, akkor eleve P1614-beli kiválasztás is. Vagyis H1614-beli kiválasztást úgy kapunk, hogy a P1614-beli kiválasztásokhoz vagy hozzávesszük a 16-ot, vagy nem, és így minden H1614-beli kiválasztást megkapunk.
2. |H327|=|P167| Ha egy H327-beli kiválasztásból elhagyjuk az esetlegesen benne szereplő 16-os számot, nyilván P167-beli kiválasztást kapunk (egy szám 32-vel osztva 7-et ad maradékul, akkor 16-tal osztva is 7-et ad maradékul). Megfordítva, ha veszünk egy P167-beli kiválasztást, akkor ha a 16 (7 maradékkal) páros számszor van meg a benne szereplő számok összegében, akkor egyben H327-beli kiválasztás is, ha pedig páratlan számszor, akkor a 16-ot hozzávéve H327-beli kiválasztást kapunk.
3. |P167|=|P1614| Megjegyezzük, hogy az 1-től 2006-ig terjedő természetes számok összegéből a 16-ot és 8-at kivonva, egy 16-tal osztva 5 maradékot adó számt kapunk. Vagyis a Q halmaz elemeinek összege kongruens 5 modul 16. |P167|=|Q167|+|Q1615|, mert ha egy P167-beli kiválasztásban nem szerepel a 8-as szám, akkor egyben Q167-beli kiválasztás is, ha pedig szerepel benne a 8-as, akkor azt elhagyva Q1615-beli kiválasztást kapunk (ha egy szám 16-tal osztva 7-et ad maradékul, akkor 8-at kivonva belőle 16-tal osztva 15-öt fog maradékul adni). Hasonlóan látható be, hogy |P1614|=|Q1614|+|Q166|. Viszont |Q167|=|Q1614|, mert egy Q167-beli kiválasztáshoz hozzárendeljük a Q-beli komplementerét (Q azon részhalmazát, amelyben a Q167-beli kiválasztásban szereplő számok kivételével minden Q-beli szám szerepel). Mivel a Q elemeinek összege 16-tal osztva 5 maradékot ad, ezért a komplementer kiválasztásban szereplő elemek összege 16-tal osztva 14-et ad maradékul. Hasonlóan igazolható, hogy |Q1615|=|Q166|. Ebből pedig következik a |P167|=|P1614| állítás.
A most bizonyított három állítást összevetve, kapjuk a feladat bizonyítandó állítását.
|
|
|
| [268] jenei.attila | 2006-12-22 22:25:28 |
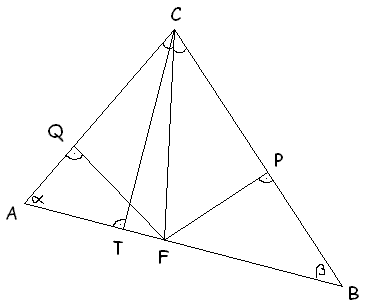
 Ez bizony szép megoldás. Most akkor jöjjön az enyém:
 és és 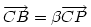 és és 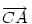 valamint valamint 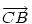 hossza legyen 1 (egyenlő hosszúak amiatt, hogy a CF szögfelező). hossza legyen 1 (egyenlő hosszúak amiatt, hogy a CF szögfelező).  . Vagyis . Vagyis  . Az együtthatókat összehasonlítva kapjuk, hogy . Az együtthatókat összehasonlítva kapjuk, hogy  (1-x)=y és (1-x)=y és  (1-y)=x, amiből (1-y)=x, amiből 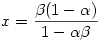 és és 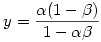 . .
A szögfelező tétel szerint  . CQ és QF szakaszok merőlegesek, ezért . CQ és QF szakaszok merőlegesek, ezért  . .  helyébe beírva a fenti kifejezést, és felhasználva hogy helyébe beírva a fenti kifejezést, és felhasználva hogy 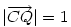 , kapjuk hogy , kapjuk hogy 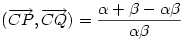 . .
Képezzük a 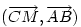 skalár szorzatot, és használjuk fel a most kapott összefüggést. skalár szorzatot, és használjuk fel a most kapott összefüggést. 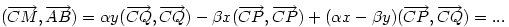 . x és y helyébe beírjuk az . x és y helyébe beírjuk az  -val és -val és  -val kifejezett alakjukat, felhasználjuk hogy -val kifejezett alakjukat, felhasználjuk hogy  , közös nevezőre hozunk, és kapjuk, hogy , közös nevezőre hozunk, és kapjuk, hogy 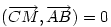 , vagyis CM merőleges AB-re. , vagyis CM merőleges AB-re.
|
| Előzmény: [267] i, 2006-12-22 20:49:47 |
|
|
|
|
| [264] jenei.attila | 2006-12-22 13:48:03 |
 A B3964 feladatra szeretnék látni egy szép, geometriai bizonyítást. Egyébként az előző hozzászólásomban szereplő feladat is érdekelne, ki hogy csinálta meg.
|
|





 -ek hasonlók, PE'O
-ek hasonlók, PE'O 


 n-1
n-1 0 ; n-1-y
0 ; n-1-y (1-x)=y és
(1-x)=y és  (1-y)=x, amiből
(1-y)=x, amiből 
 CQ=CP és FQ=FP.
CQ=CP és FQ=FP.  =ATC
=ATC ACT
ACT