Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[152] lorantfy	2004-05-05 19:29:18
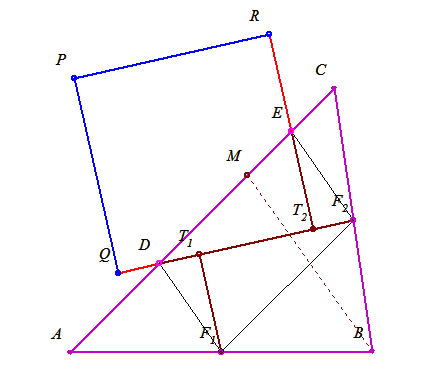
Kedves Géza és Fórumosok! Valóban a B-ből induló magasságra nincs szükség, ez volt a félrevezetés, ui. egy "átlagos" hegyesszögű $\Delta$ -ben a talppontja elég közel esik ahhoz az M ponthoz amire négyzetet kapunk. A DF₁F₂E paralelogramma DF₂ átlója egyenlő a RPQT₂ téglalap QT₂ oldalával. Tehát, ha meg tudnánk szerkeszteni a leendő négyzet x oldalát, akkor F₂ pontból kimetszhetnénk vele AC-ből a D pontot. Ezután A pont tükörképe D-re adja az M pontot. 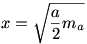$x=\sqrt{\frac{a}{2}m_a}$ , tehát egyszerű mértani közép szerkesztéssel megkaphatjuk x-t az egyik oldal feléből és a hozzá tartozó magasságból.

Előzmény: [151] Kós Géza, 2004-05-05 13:55:04

[151] Kós Géza

2004-05-05 13:55:04

Ahogy látom, a B-ből induló magasságra nincs is szükség. Az M pont bárhol lehet az AC oldalon, feltéve, hogy a T₁ és T₂ pontok nem kerülnek a DF₂ szakaszon kívülre.

46b. feladat: Szerkesszük meg az AC oldalon azt az M pontot, amire az RPQT₂ téglalap négyzet lesz.

Előzmény: [144] lorantfy, 2004-05-02 10:39:46

[150] lorantfy

2004-05-05 13:33:53

Szabályos $\Delta$ esetén, a lenti ábra jelöléseivel, AB=1 esetén:

$RT_2=\frac{\sqrt3 \sqrt7}{7} \neq QT_2=\frac{\sqrt7}{4} \quad T_{PQT_2R}= \frac{\sqrt3}{4}=T_\Delta$

Előzmény: [149] Hajba Károly, 2004-05-04 21:38:33

[149] Hajba Károly	2004-05-04 21:38:33
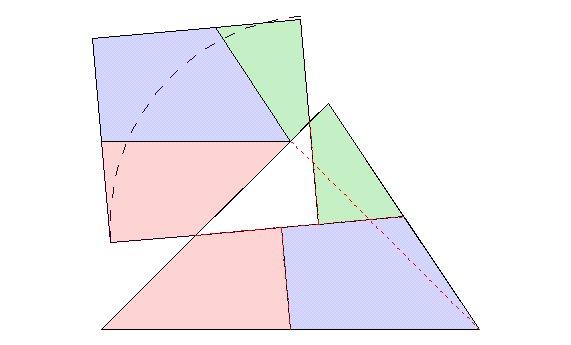
Kedves Géza és László! Ha most politikus lennék, azt mondanám: Nem is mondtam, hogy négyzet! :o) Az igazság az, hogy a területegyezőségekben mélyedtem el, s felelőtlen, slendrián kijelentésemet főleg erre értettem, ami persze igaz, de tény, hogy nem vetődött fel bennem a nemnégyzet lehetősége. Tehát, ha egy ácshajszálnyival is, de nem feltétlenül négyzet, mely a mellékelt ábrából is kitűnik. HK

Előzmény: [147] Kós Géza, 2004-05-04 12:48:51

[148] lorantfy	2004-05-04 14:07:49
Kedves Géza, Károly és Fórumosok! Gézának igaza van! Az ábra félrevezető lehet. Szabályos $\Delta$ esetén gyorsan utánna számolhatunk igaz-e az állítás.

Előzmény: [147] Kós Géza, 2004-05-04 12:48:51

[147] Kós Géza

2004-05-04 12:48:51

Az ábrák sokszor becsapnak, nem szabad hinni nekik. :-)

Az első kérdésre a válasz nem. Téglalap, de nem négyzet.

Előzmény: [145] Hajba Károly, 2004-05-04 12:27:23

[146] Hajba Károly

2004-05-04 12:33:58

47. feladat:

Létetik-e olyan a $\in$ N⁺, melynek reciproka felbontható véges számú különböző prím reciprokösszegére?

[145] Hajba Károly

2004-05-04 12:27:23

Kedves László!

Az ábrád önmagáért beszél. A levezetését ráhagyom egy fiatal titánra. :o)

Előzmény: [144] lorantfy, 2004-05-02 10:39:46

[144] lorantfy

2004-05-02 10:39:46

Kedves Fórumosok!

A következő feladat Bólyai Farkas egy híres átdarabolásából született.

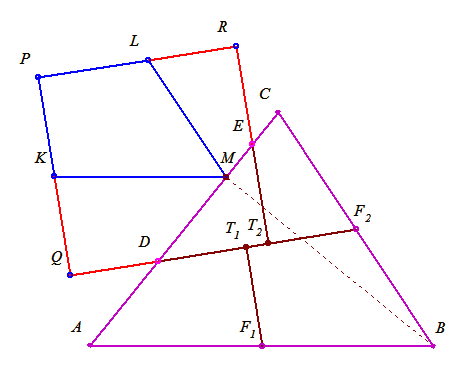
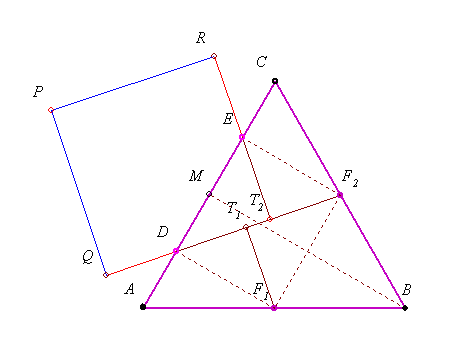
46. feladat: Legyen ABC hegyesszögű $\Delta$ AB oldalának felezőpontja F₁, BC oldalának felezőpontja F₂ és a B csúcsból induló magasság talppontja M.

Legyenek AM és MC felezőpontjai D és E. Húzzuk meg a DF₂ egyenest és állítsunk rá merőlegest az F₁ és E pontokból. Ezek talppontjai legyenek T₁ és T₂. Tükrözzük a T₁ pontot D-re, a T₂ pontot E-re. A tükörképek legyenek Q és R. Ezekben a pontokban állított merőlegesek metszéspontja legyen P.

Igyaz-e, hogy a keletkezett négyszög négyzet és területe megegyezik az ABC $\Delta$ területével?

[143] lorantfy	2004-05-02 10:05:37
Kedves Károly! Ezt a kis feladatot amolyan EU-belépési tesztnek szántam. Gratulálok! Te már beléphetsz! Rajzos megoldás: a sárgára szinezett részek a kék és piros részt is a terület felére egészíti ki.

Előzmény: [142] Hajba Károly, 2004-05-02 00:26:06

[142] Hajba Károly

2004-05-02 00:26:06

Megoldás a 45. feladatra:

Egy-egy háromszög területe a négyzet területének felével egyenlő, vagyis a két háromszög területe épp a négyzetével egyenlő. (azaz fehér + 2*piros = négyzet) Így amennyi az átfedésük területe (piros), annyinak kell lennie a le nem fedett területnek (kék) is.

Ezt a feladatot annyiban lehet általánosítani, hogy akár téglalapon és bármely két oldalára felvett háromszöggel is igaz.

Előzmény: [141] lorantfy, 2004-05-02 00:04:39

[141] lorantfy	2004-05-02 00:04:39
45. feladat: Egy négyzet két szomszédos oldalán felvettünk egy-egy tetszőlegesen választott pontot, melyet összekötöttünk a szemközti oldal végpontjaival. Igazoljuk, hogy az így keletkezett pirosan színezett síkidom területe megegyezik a kékkel színezett síkidomok területeinek az összegével!

[140] Suhanc

2004-04-18 18:59:55

Kedves Csimby!

Hát ezek nem sokáig maradtak életben... :)

Köszi a megoldásokat!

A 45. feladaton érdekesnek hangzik... gondolkodok rajta!

Előzmény: [139] Csimby, 2004-04-18 16:06:00

[139] Csimby

2004-04-18 16:06:00

43. feladat megoldása:

n=(10^2k+1-1)/9-2*(10^k+1-1)/9=(10^2k+1-2*10^k+1+1)/9=((10^k+1-1)/3)²

Mivel 10^k+1-1 csupa 9-esből áll, osztható 3-mal, tehát (10^k+1-1)/3 egész szám, n pedig négyzetszám!

44. feladat megoldása:

n(n+1)(n+2)(n+3)=6n+11n²+6n³+n⁴, ugyanakkor 6n+11n²+6n³+n⁴+1=(n²+3n+1)²

Két négyzetszám különbsége pedig nem lehet 1 (kivéve, ha az egyik a 0, hiszen (n+1)²-n²=2n+1 ami csak n=0-ra egyenlő 1-gyel).

Hasonlít a 43. feladathoz a tanárképző főiskolák idei Péter Rózsa matematika versenyének 1. feladata (legyen ez a 45. feladat):

A=177...76 (2k+3 jegyű), B=355...52 (k+2 jegyű). Biz. be, hogy 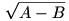$\sqrt{A-B}$ természetes szám és mondjuk meg, hogy hány jegyű.

Előzmény: [138] Suhanc, 2004-04-17 22:00:51

[138] Suhanc

2004-04-17 22:00:51

Kedves Fórumosok!

Az alábbi két feladattal Bonifert Domonkos: Néhány tipikus problémaszituáció matematikából c. könyvében találkoztam.

Szerintem okozhatnak néhány kellemes percet, mégha komoly fejtörést nem is...

43.feladat Lássuk be, hogy n=111...111-222...222

(2k db 1-es, és k db 2-es) minden k>o egészre négyzetszámot ad!

44.feladat Lássuk be, hogy n(n+1)(n+2)(n+3) nem lehet négyzetszám, ha n poz. egész!

[137] nadorp

2004-04-14 08:22:25

Kedves Csimby !

A 41. feladatra inkább ebben a topicban adok egy megoldást, mert a bizonyítás algebrai, bár az ötletet a háromszögbe írható körhöz húzott érintőszakaszok adták.

Legyen a=y+z, b=x+z, c=x+y. Ekkor az egyenlőtlenség az alábbi alakba írható:

(y+z)²^.2x+(x+z)²^.2y+(x+y)²^.2z $\leq$ 3(y+z)(x+z)(x+y)

6xyz $\leq$ x²y+xy²+x²z+xz²+y²z+yz² vagy "szebben" írva

$xyz\leq\frac{x^2y+xy^2+x^2z+xz^2+y^2z+yz^2}6$

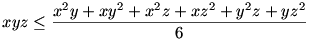
A fenti egyenlőtlenség pedig azonnal következik a számtani és mértani közép közötti összefüggésből.

Előzmény: [134] Csimby, 2004-04-11 22:10:02

[136] Csimby	2004-04-11 22:21:43
A 41. és 42. feladatot a Geometria témába akartam rakni, de most már mindegy...

[135] Csimby	2004-04-11 22:16:40
42.feladat Bizonyítsuk be, hogy minden húrnégyszög szétvágható n db. húrnégyszögre, ha n $\ge$ 4 poz. egész.

[134] Csimby

2004-04-11 22:10:02

41. feladat Bizonyítsuk be, hogy ha a,b,c egy háromszög oldalai, akkor:

a²(-a+b+c)+b²(a-b+c)+c²(a+b-c) $\le$ 3abc

[133] Suhanc

2004-04-10 23:11:06

Kedves László!

Bevallom őszintén, összetörtél bennem egy elképzelést erről feladatról...:)

Nem gondoltam, hogy ilyen elegáns alakban is megkaphatjuk a megoldást, és sok apró lépegetés során hoztam ki egy olyan alakot,amiben már csak a három oldal négyzete szerepel... erre gondoltam, amikor "csavargatásról" írtam...

Hát ez van! ;))

De mindenképp tanulságos volt nekem, köszönöm a megoldást!

[132] lorantfy

2004-03-23 10:47:25

40. feladat megoldása: Hát egyenlő oldalú nem lehet a $\Delta$ mert akkor a nevező 0 lenne. Egyenlő szárú is csak úgy, ha b az egyik szár. Kicsit átalakítva:

(a²-c²-b²)(a+c)²=0

Így aztán derékszögű lesz a $\Delta$ , az átfogója: a.

Előzmény: [131] Suhanc, 2004-03-20 15:48:51

[131] Suhanc

2004-03-20 15:48:51

Kedves Veresh!

Köszönöm a megoldást!:) Az esetszétválasztás szerintem nem szükséges, elég azt mondani, hogy "végtelen sok ilyen tulajdonságú szám van, és csak véges sok maradék osztály..." de a Te megoldásod ezt sokkal elegánsabban tálalja.

Egy matematika tesztverseny 10. osztályos feladatsorának feladata volt az alábbi feladat. Nem bonyolult, mégis szép, ahogy csavargatod, hogy kijöjjön a kívánt eredmény...:)

40.Feladat: Egy háromszög a, b, c oldalaira teljesül, hogy $\frac {3b^2(a-c)^2+12ab^2c}{a^4+2a^3c-c^4-2ac^3}=3$ Mit mondhatunk el ekkor a háromszögről?

Előzmény: [130] veresh, 2004-03-15 23:13:30

[130] veresh

2004-03-15 23:13:30

39. feladat megoldása

Legyen n=123456789. Tekintsük a következő sorozatot:

a₁=1, a₂=11, a₃=111, ..., a_n=1...1

(1) Ha

$\exists$ i $\in$ {1,...,n}: n|a_i,

akkor készen vagyunk.

(2) Ellenkező esetben (legfeljebb) n-1 maradékosztály van. És mivel a sorozat n tagú, ezért a skatulya-elv szerint van a sorozatnak két olyan tagja, amely ugyanabba a maradékosztályba tartozik; formálisan:

$\exists$ i>j: a_i $\equiv$ a_j(mod n) <==> n|(a_i-a_j)

a_i-a_j = 1...10...0 = 1...1^.10^j

(ahol i-j db. 1-es és j db. 0 számjegy van). És mivel

$\forall$ j $\in$ N: (n,10^j) = (3²^.3607^.3803,10^j) = 1

Ezért n|1...1 (i-j db. 1-es). Azaz

$\exists$ k $\in$ N: n^.k=1...1

Előzmény: [129] Suhanc, 2004-03-15 20:17:43

[129] Suhanc

2004-03-15 20:17:43

Kedves László!

Köszöm szépen! Még pár év fórum, és megismerem az egész klaviatúrát...:)

Ez a feladat szerintem nagyon tanulságos, és szép:

39.Feladat. Igazoljuk, hogy 123456789-nek van olyan pozitív egész többszöröse, amelyben csupa 1-es szerepel!

Előzmény: [128] lorantfy, 2004-03-15 12:28:59

[128] lorantfy

2004-03-15 12:28:59

Kedves Suhanc!

Kösz a megoldást! Sokszor jól alkalmazható trükk prímszámos feladatokban, hogy a 3-nál nagyobb prímszámok p=6k $\pm$ 1 esetleg p=12n $\pm$ 1 vagy p=12n $\pm$ 5 alakban írhatók!

Az oszhatóság jelet simán be lehet gépelni: AltGr+w kombinációval.

Előzmény: [127] Suhanc, 2004-03-15 08:19:13

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?