| [283] lorantfy | 2005-07-12 22:12:13 |
 Igazad van! A szokás szerint a következő születésnapig az előző életkor számít és ezt a feladat szövege megengedi. Nem erre gondoltam a megfogalmazáskor, de most rájöttem, hogy akkor lenne igazán jó a feladat ha csak egy megoldása lenne, a Te elképzelésed szerinti.
|
| Előzmény: [281] jonas, 2005-07-12 19:46:08 |
|
| [282] Suhanc | 2005-07-12 22:06:32 |
 Kedves László!
Ha nem rontottam el, úgy néz ki, az 1900 és 2000 között születettek közül csak az 1984-re stimmel a feladat állítása (Ha szigorú értelemben vesszük. Jonas elgondolását nem írtam bele a programba). Szóval így kissé meghökkentő a feladat végeredménye...kétszeresen is...
|
| Előzmény: [280] lorantfy, 2005-07-12 18:02:36 |
|
| [281] jonas | 2005-07-12 19:46:08 |
 Miért nem jó az 1979? Ha a szülő mondjuk 1979. októberben született, a gyereke pedig 2002. márciusában, akkor 2006. júliusában a szülő 26 éves, és 1+9+7+9=26, de a gyereke már 4 éves, és 2+0+0+2=4.
|
| Előzmény: [280] lorantfy, 2005-07-12 18:02:36 |
|
|
| [279] jonas | 2005-07-12 15:01:41 |
 Igen, 1979-ben született, a gyermeke pedig 2002-ben. (Nem olyan valószínű, de esetleg az is előfordulhat, hogy 1984-ben született, a gyereke szintén 2002-ben.)
|
| Előzmény: [278] lorantfy, 2005-07-11 12:08:37 |
|
| [278] lorantfy | 2005-07-11 12:08:37 |
 70. feladat: Valaki azt állítja, hogy jövő évben (2006) ő és gyermeke is annyi ídős lesz mint születési évszámuk számjegyeinek összege. Igaza lehet?
|
|
| [277] lorantfy | 2005-04-16 13:54:05 |
 Kedves Suhanc és Fórumosok!
Bizonyítottnak kell tekintenek a gondolatátvitellel való információátadás lehetőségét :-), ugyanis az előző hozzászólásom végére odagondoltam, hogy akkor gyártsatok hasonló feladatokat.
Ezen kívül gratula az 55. feladat megoldásaiért! Nagyon tetszettek.
|
| Előzmény: [276] Suhanc, 2005-04-16 12:21:11 |
|
| [276] Suhanc | 2005-04-16 12:21:11 |
 69.Feladat Bizonyítsd be, hogy:
17|33n+152n+1+25n+111n
|
|
| [275] lorantfy | 2005-04-15 07:50:54 |
 Kedves Csimbi!
Kösz az ügyes és gyors megoldást. Végülis az a lényeg, hogy ha két szám azonos maradékot ad, k-val osztva, akkor n-edik hatványuk is azonos maradékot ad.
|
| Előzmény: [270] Csimby, 2005-04-13 16:48:53 |
|
| [274] Suhanc | 2005-04-14 20:56:45 |
 Kedves Sirpi és Fálesz Mihály!
Köszönöm a megoldásotokat! Igazából már lemondtam róla, hogy bárkit is érdekeljen a feladat... Sirpi, említettél egy közepes megoldást, ami szerintem megegyezik az én megoldásommal. Mindenesetre akkor én azt engedelmeddel "pofátlanul beírnám", szerintem van üzenete...
Megfelelő módon osztjuk részekre a baloldalon lévő mennyiségeket, és ezekből fogjuk a jobb oldal tagjait a számtani- mértani közepek közötti egyenlőtlenség egítségével becsülni.
Eredetileg: a3b+b3c+c3a a2bc+ab2c+abc2 a2bc+ab2c+abc2
Ekkor:
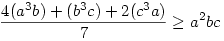

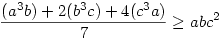
E három egyenlőtlenséget összeadva épp a bizonyítandó állítást kapjuk...
|
| Előzmény: [273] Sirpi, 2005-04-14 14:24:06 |
|
| [273] Sirpi | 2005-04-14 14:24:06 |
 Hát igen, ez jóval egyszerűbb megoldás. Viszont igaz, hogy a másik hosszú, meg számolós, de az enyém :-) Közben rájöttem én is egy másik, nem ennyire számolós megoldásra.
Osszuk le mindkét oldalt abc-vel (ha valamelyik szám 0, akkor triviálisan igaz az egyenlőtlenség):
a2/c+b2/a+c2/b a+b+c a+b+c
Átrendezve:
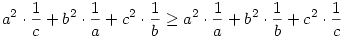
Mindkét oldalon az a2,b2,c2 számok vannak páronként összeszorozva az 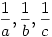 számokkal, és össze vannak adva a szorzatok, csak más sorrendben vannak összepárosítva a két oldalon. Ismert tétel (rendezési tételnek, vagy Szűcs Adolf-tételnek is hívják), hogy egy ilyen szorzat akkor lesz maximális, ha a két összeszorzandó sorozat azonos módon van rendezve, akkor lesz a legkisebb, ha ellentétes módon, ebből következően az összes többi permutáció e kettő közt fog elhelyezkedni. számokkal, és össze vannak adva a szorzatok, csak más sorrendben vannak összepárosítva a két oldalon. Ismert tétel (rendezési tételnek, vagy Szűcs Adolf-tételnek is hívják), hogy egy ilyen szorzat akkor lesz maximális, ha a két összeszorzandó sorozat azonos módon van rendezve, akkor lesz a legkisebb, ha ellentétes módon, ebből következően az összes többi permutáció e kettő közt fog elhelyezkedni.
A jobb oldalon fordított sorrendben van rendezve a két számhármas (ha pl. a2 b2 b2 c2, akkor 1/a c2, akkor 1/a 1/b 1/b 1/c), így a bal oldal legalább akkora, mint a jobb. 1/c), így a bal oldal legalább akkora, mint a jobb.
|
|
| [272] Fálesz Mihály | 2005-04-14 14:03:12 |
 Szia Sirpi,
A megoldást ismertem, ezért nem írtam le eddig. (A 83-as párizsi diákolimpián a legnehezebb feladatot, amire a teljes magyar csapat összesen 1 pontot szerzett, erre az egyenlőtlenségre lehetett visszavezetni egy kis trükkel.)
(a3b+b3c+c3a)-(a2bc+ab2c+abc2)=
=ab(a-c)2+bc(b-a)2+ca(c-b)2 0. 0.
F.M. :-)
|
| Előzmény: [271] Sirpi, 2005-04-14 11:16:40 |
|
| [271] Sirpi | 2005-04-14 11:16:40 |
 Na, akkor a rég eltemetett 55. feladatról írnék, ami úgy szólt, hogy ha a,b,c 0, akkor a3b+b3c+c3a 0, akkor a3b+b3c+c3a a2bc+ab2c+abc2. a2bc+ab2c+abc2.
Kijött közepekkel is, de ha nem akarok nagyágyúkat használni, akkor ki lehet direkt módon is hozni. Első észrevétel, hogy ha a=b=c=0, akkor triviálisan igaz az állítás. Ha meg nem, akkor szorozzunk fel (a+b+c)-vel:
(a+b+c)(a3b+b3c+c3a) abc(a+b+c)2 abc(a+b+c)2
Elvégezve a beszorzást mindkét oldalon 9-9 tagot kapunk, amiből 3 egyezik:
a4b+ab3c+a2c3+a3b2+b4c+abc3+a3bc+b3c2+ac4 a3bc+ab3c+abc3+2a2b2c+2a2bc2+2ab2c2 a3bc+ab3c+abc3+2a2b2c+2a2bc2+2ab2c2
Rendezve:
(a4b+b3c2-2a2b2c)+(b4c+c3a2-2ab2c2)+(c4a+a3b2-2a2bc2) 0 0
Ez pedig nyilvánvalóan igaz, mert ez átírható a következő alakra:
b(a2-bc)2+c(b2-ac)2+a(c2-ab)2 0 0
Egyenlőség akkor áll fenn, ha minden tag 0. Minden tag egy szorzat, ezért az egyenlőségnek az a feltétele, hogy minden tényező valamelyik tagja 0. Nézzük meg az eredeti egyenletet abban az esetben, ha pl. c=0, ekkor a bizony1tandó egyenlet az a3b 0 alakra egyszerűsödik. Vagyis ha van nulla a számok közt, akkor egyenlőség áll fenn, amennyiben van köztük még legalább egy másik nulla is. 0 alakra egyszerűsödik. Vagyis ha van nulla a számok közt, akkor egyenlőség áll fenn, amennyiben van köztük még legalább egy másik nulla is.
Ha nincs nulla a számok közt, akkor pedig az a2=bc,b2=ac,c2=ab egyenlőségek mindegyikének kell teljesülnie, de ha feltesszük, hogy c a legnagyobb, és c2=ab, abból rögtön következik, hogy a=b=c. Tehát az (a,a,a) és az (a,0,0) számpárok esetén van egyenlőség.
|
| Előzmény: [189] Suhanc, 2004-09-22 20:12:09 |
|
| [270] Csimby | 2005-04-13 16:48:53 |
 26n-1+5n.32n+2 akkor és csak akkor osztható 19-cel, ha a 2-szerese is osztható vele, tehát vizsgáljuk a 2-szeresét: 26n+2.5n.32n+2=64n+2.5n.9.9n
2.9 -1 (mod 19) -1 (mod 19)  64n+2.5n.9.9n 64n+2.5n.9.9n 64n-45n 64n-45n
64n-45n=(64-45)(64n-1+64n-2.45+64n-3.452+...+64.45n-2+45n-1)
64-45=19, tehát készen vagyunk.
|
| Előzmény: [269] lorantfy, 2005-04-13 09:25:54 |
|
| [269] lorantfy | 2005-04-13 09:25:54 |
 68. feladat: Bbh. minden n-re 19 osztója 26n-1+5n.32n+2-nek !
|
|
| [268] Lóczi Lajos | 2005-03-29 22:26:50 |
 Aki a (határozatlan) integrálokkal szeretne egy kicsit játszani (és éppen nincs szimbolikus programcsomagja kéznél), azoknak ajánlom a http://integrals.wolfram.com/ címet. Ott meglátod a kérdésedre az általános választ, ami speciális függvényt tartalmaz. (Ezekről egy hatalmas gyűjtemény l. pl. a http://functions.wolfram.com/ címen.) Persze minden konkrét k-ra és n-re az integrál elemien kiszámítható. DE, a paraméterekkel csínján kell azért bánni, hiszen itt ugye hallgatólagosan azt FELTÉTELEZTÜK, hogy k és n pl. pozitív egészek. De már a k=1 és n=-1 esetben is teljesen más alakú lesz a primitív függvény, mint amit írtál. (Sőt, ugye még ott vannak az a és b paraméterek is...nulla vagy nem nulla, stb.)
|
| Előzmény: [266] tudniakarok, 2005-03-27 11:58:50 |
|
| [267] lorantfy | 2005-03-27 12:03:23 |
 Na ez rendben van! Hát ebből látszik, hogy ha be van szorozva a belső fgv. deriváltjának megfelelő x hatvánnyal akkor könnyű a dolgunk. Ebből azt is lehet sejteni, miért nehéz, ha nincs beszorozva a deriválttal.
|
| Előzmény: [264] tudniakarok, 2005-03-27 00:50:32 |
|
|
|
| [264] tudniakarok | 2005-03-27 00:50:32 |
 Kicsi a világ,főleg a neten!:) Bár szégyen szemre nekem nem ugrik be az ismerettség,de elég meggyőző a sporttárs megszólítás,úgyhogy biztos ismerjük egymást,csak rossz az arcmemóriám!bocsánat. A feladatot eddig könnyebb megoldani mint beírni szépen:)
![\int x\big(ax^2+b)^n dx=\bigg[\frac{(ax^2+b)^{n+1}}{(n+1)2a}\bigg]](keplet.cgi?k=0DB8EB737E31BC04)
|
| Előzmény: [263] lorantfy, 2005-03-26 22:30:21 |
|
|
| [262] tudniakarok | 2005-03-26 18:21:25 |
 Köszönöm a megerősítést!(a nagy könyvben nem találtam meg:) Gondoltam hogy a kérdésem belebonyolódik a matamatika olyan részeibe, ami egyelőre távol áll az én tudásomtól! Na de mind1!
|
| Előzmény: [261] lorantfy, 2005-03-26 01:09:14 |
|
| [261] lorantfy | 2005-03-26 01:09:14 |
 Ez jól van így. Majdnem olyan, mint ahogy a nagykönyvekben meg van írva. Még egy +C-t szoktak hozzáírni, minthogy ez határozatlan integrál, szóval egy konstans erejéig határozatlan. Ha visszaderiválsz a konstans eltűnik, így bármi lehet.
Arra a kérdésre, mi van, ha a kerek zárójelen belül (axk+b)-van, a válasz: baj. Ettől kicsit elbonyolódik a dolog.
|
| Előzmény: [260] tudniakarok, 2005-03-25 23:12:48 |
|
| [260] tudniakarok | 2005-03-25 23:12:48 |
 Kérlek segítsetek! Házi volt a csonkakúp térfogatának bizonyítása integrálszámítással,na most én lusta voltam bontogatni a zárójeleket,így összetett fv. primitív fv.-ét kerestem,kijött a jó képlet,a tanárom szerint lehet hogy csak véletlen,mert hogy ő nem érti(vagy csak nem akarja gyötörni magát)! Na de a lényeg,tehát vmi ilyesmi jött ki általánosan:
![\int{(ax+b)^n}dx=\bigg[\frac1a\frac{(ax+b)^{n+1}}{n+1}\bigg]](keplet.cgi?k=32B76B09D626FA45) szerintem jó,de ha találtok vmi hibát lécci közöljétek,mert még nem csináltam túl sok ilyen példát!Előre is köszi! Ja és még egy kérdés: mi van akkor ha az intergrandusban a változó nem elsőn hanem k-adikon van,erre még nem jöttem rá!? szerintem jó,de ha találtok vmi hibát lécci közöljétek,mert még nem csináltam túl sok ilyen példát!Előre is köszi! Ja és még egy kérdés: mi van akkor ha az intergrandusban a változó nem elsőn hanem k-adikon van,erre még nem jöttem rá!?
|
|
|





 a2bc+ab2c+abc2
a2bc+ab2c+abc2 
 1/b
1/b

 -1 (mod 19)
-1 (mod 19)  64n+2.5n.9.9n
64n+2.5n.9.9n
