Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[308] Lóczi Lajos	2005-09-18 20:28:11
Pontosan melyik kifejezés(ek)re gondolsz, melyik képletben, hogy felveszi a 3/2 értéket?
Előzmény: [306] hobbymatekos, 2005-09-17 23:37:21

[307] Lóczi Lajos

2005-09-18 20:24:29

Nem értem, mi nem stimmel.

A gömbi koordinátákat a régi x,y,z változók helyére helyettesítjük, a konstans 1 nem tartalmaz ilyet, nem kell semmilyen gömbfelületként sem felfogni, csak puszta számként.

Előzmény: [301] hobbymatekos, 2005-09-16 21:06:45

[306] hobbymatekos	2005-09-17 23:37:21
Mutassuk meg,hogy $\frac{3}{2}$ értéket is felveszi. a) adjuk meg, ezen pontok mértani helyét b) döntsük el, hogy felülről korlátos e a kifejezés c) ha igen, adjuk meg a felső korlátot
Előzmény: [304] Suhanc, 2005-09-17 20:30:11

[305] Káli gúla	2005-09-17 21:16:39
Az utolsó egyenlőtlenség jobb oldalán 15 lesz (de apró betűvel az is elfér a margón :-)
Előzmény: [304] Suhanc, 2005-09-17 20:30:11

[304] Suhanc

2005-09-17 20:30:11

Az említett margó(m):

Csimbyhez hasonlóan én is a számlálóknak adtam új jelölést, ezáltal a már említett

$\frac{a}{2b+c}+\frac{b}{2c+a}+\frac{c}{2a+b} \ge 1$

egyenlőtlenséget kapva. Ezután viszont inkább megint bevezettem egy új jelölésrendszert, remélve, hogy a feltételek felrúgása nélkül kaphatunk egyszerűbb alakot:

2b+c=p 2c+a=q 2a+b=r

alapján kapjuk, hogy

$\frac{4r-2p+q}{9p}+\frac{4p-2q+r}{9q}+\frac{4q-2r+p}{9r}\ge 1$

Melyet megfelelő módon átalakítva kapjuk, hogy:

$4( \frac{r}{p}+\frac{p}{q}+\frac{q}{r})+(\frac{q}{p}+\frac{r}{q}+\frac{p}{r}) \ge 1$

Mivel p, q, r nemnegatív számok, a két zárójelet számtani-mértani középpel lebecsülve a bizonyítandó állítást kapjuk.

Előzmény: [300] Lóczi Lajos, 2005-09-15 20:53:41

[303] Suhanc

2005-09-17 20:15:14

Kedves Mindenki!

Kissé megkéstem ezzel a hozzászólással. Így utólag is szeretném megköszönni mindenkinek az érdekes megoldásokat és hozzájuk kapcsolódó hozzászólásokat. Azontúl, hogy általánosságban is megmozgatta az állóvizet, nekem személyesen sok újat mutatott (pl: az emlegetett Titu-lemma). A konkrét sztorit eddig szándékosan nem írtam le a feladathoz: matektáborban ifiként tevékenykedtem, egy 9. osztályos tanuló pedig felajánlott nekem egy tábla csokit, ha megoldom belátható időn belül ezt a feladatot. A megoldás megbeszélése után említette, hoyg ő ezt Cauchy-Schwarz-Bunyakovszkij egyenlőtlenséggel meg tudja csinálni rövidebben. "Egy tábla csokiért elárulom"-mosolygott. Azonban a csoki, amelyret már gondolatban szétosztottunk az ifistársak közt, nagyon hívogató volt, ezért lemondtam (szégyen, gyalázat) a megoldásról. Reméltem, hogy elő fog kerülni...

[302] hobbymatekos	2005-09-16 22:50:28
Erről (elemi)algebrailag annyi mondható ameddig eljutottatok. Van pontosan 6 kúp amik csúcsa az origó, ezeken a kifejezés (skalár-vektor) fv. értéke 1 a kúpok és a koo sikokkal való metszeteiként adódó alkotók mentén. A kérdés: mikor nagyobb mint 1 és mikor kisebb. Ez csak algebrailag nem oldható meg.Ez a feladat Tenzoranalizis és diff.geometria. eszközökkel kezelhető.(Riemann tér) Euklideszi normában és derékszögü koo.rsz. reprezentációban is szemléletes. Adottak a helyvektorok, valamint három irány. Keressük azt a tartományt amelyikben teljesül, hogy a vektor egy adott koo. sikra való vetületvektorai hossznégyzeteinek a sihoz redelt adott (most állandó) irányra való (merőleges) vetületvektorának hossznégyzeteivel vett hányadosainak összege legalább 1.
Előzmény: [289] Suhanc, 2005-08-29 09:37:23

[301] hobbymatekos

2005-09-16 21:06:45

Nem ok:(.

K(x,y,z)-ről

áttérünk gömbi koo. rendszerbe, az azonosan egyből mi lesz? Azonosan 1 sugarú gömbfelület. Vagyis ?.

Előzmény: [290] Lóczi Lajos, 2005-09-01 16:23:34

[300] Lóczi Lajos	2005-09-15 20:53:41
Lehet, hogy úgy ujjgyakorlat, mint Fermat mondása, hogy túl kicsi a margó, hogy épp odaírja a bizonyítást :-)
Előzmény: [296] jenei.attila, 2005-09-15 09:50:21

[299] Lóczi Lajos

2005-09-15 20:37:27

Aprócska pontosítás az előző hozzászólásokhoz:

Cauchy-Schwarz helyesen, "t" nélkül. (Schwartz az másik matematikus volt.)

Előzmény: [298] Kemény Legény, 2005-09-15 16:38:00

[298] Kemény Legény	2005-09-15 16:38:00
Kedves Attila! Valóban nem meglepő, hogy nem találtál a 'Titu-lemmá'-ról semmit. A fenti tételt/elnevezést a román matek olimpiai csapattal való közös felkészülés során hallottuk.Ők ezt Titu Andreiescu után hivják igy (ő több évig volt az amerikai olimpiai csapat vezetője,ha nem tévedek). Amint arra Káli gúla is rámutatott: a 'Titu-lemma' valóban a Cauchy-Schwartz-Bunyakovszkij-egyenlőtlenségből következeik, sőt azzal ekvivalens is,azonban annál összehasonlithatatlanul 'felhasználóbarátabb'.Konkrét esetekben jóval könnyebben fel lehet ismerni ennek az alkalmazási lehetőségét,és persze a tagokról is látszik,hogy mely számokra kell felirni azt. Suhanc feladatában pl. rögtön látszott ez a lehetőség, és általában is kevesebb ötletességet igényel, mint a C-S-B-egyenlőtlenség felirása.Talán épp emiatt is merült fel ez a 'lemma' a felkészülés során, a versenyeken ugyanis időt lehet vele nyerni,és nem kezd el az ember más,nehezebben járható utakon elindulni.... Véleményen szerint semmiképpen sem árt ismerni a CSB eme átirt alakját,és olyan esetekben is felfedezni azt,ahol nem látszik a CSB nyilvánvaló használata...
Előzmény: [296] jenei.attila, 2005-09-15 09:50:21

[297] Káli gúla

2005-09-15 11:57:01

Ha a Cauchy-Schwartz egyenlőtlenségben

$\sum x_i^2 \sum y_i^2 \ge (\sum x_i y_i)^2$

a_i=x_iy_i-t helyettesítünk, akkor

$\sum \frac{a_i^2}{y_i^2} \sum y_i^2 \ge (\sum a_i)^2 , \quad azaz \quad \sum \frac{a_i^2}{y_i^2} \ge \frac {(\sum a_i)^2}{\sum y_i^2}$

Előzmény: [296] jenei.attila, 2005-09-15 09:50:21

[296] jenei.attila	2005-09-15 09:50:21
Tudnátok bővebb információval szolgálni a Titu-lemmával kapcsolatban? Ezelőtt soha nem hallottam róla, sőt a neten sem találtam semmit. Kíváncsi lennék Suhanc megoldására is, ha már szerinte ez csak ujjgyakorlat.
Előzmény: [295] SAMBUCA, 2005-09-12 00:34:20

[295] SAMBUCA

2005-09-12 00:34:20

Sziasztok!

A titu lemmáról jut eszembe: Csak nem adja be az olimpiai 3. feladatot?! Dehogynem:

xzy $\ge$ 1 és az kell, hogy $\frac{x^5-x^2}{x^5+y^2+z^2}+\frac{y^5-y^2}{y^5+z^2+x^2}+\frac{z^5-z^2}{z^5+x^2+y^2}\ge 0$ . Első lépésként átalakítunk: x⁵-x² helyére: x⁵+y²+z²-(x²+y²+z²), így az első tört: $1-\frac{x^2+y^2+z^2}{x^5+y^2+z^2}$ hasonlóan a másik kettő, igy azt kell belátni, hogy: $3\ge (x^2+y^2+z^2)*\left(\frac{1}{x^5+y^2+z^2}+\frac{1}{y^5+z^2+x^2}+\frac{1}{z^5+x^2+y^2}\right)$ És most jön a trükk: szorozzunk be (x²+y²+z²)-tel!

A baloldalon 3*(x²+y²+z²) lesz, a jobboldalon: $\frac{(x^2+y^2+z^2)^2}{x^5+y^2+y^2}$ alakú tagok lesznek, amiket Titu-val tudunk felülről becsülni: $\frac{(x^2)^2}{x^5}+\frac{(y^2)^2}{y^2}+\frac{(z^2)^2}{z^2} \ge \frac{(x^2+y^2+z^2)^2}{x^5+y^2+z^2}$ azaz $\frac{1}{x}+y^2+z^2 \ge \frac{(x^2+y^2+z^2)^2}{x^5+y^2+z^2}$ hasonlóan a másik két törtre, ezeket összegezve: $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}+2(x^2+y^2+z^2) \ge Jobboldal.$ Elég lenne belátni, hogy $3(x^2+y^2+z^2)\ge \frac{1}{x}+\frac{1}{y}+\frac{1}{z}+2(x^2+y^2+z^2)$ azaz, hogy $x^2+y^2+z^2 \ge \frac{1}{x}+\frac{1}{y}+\frac{1}{z}$ . Nemes egyszerüséggel felszorzunk,igy az kell, hogy: xyz(x²+y²+z²) $\ge$ xy+yz+zx, ez pedig xyz $\ge$ 1 és a rendezési tétel miatt igaz.

QED

SAMBUCA

[294] Kemény Legény

2005-09-09 10:44:10

A megoldás a 'Titu-lemma' használatával kicsit egyszerűbben is kijön: könnyen ellenőrizhető (pl.felszorzással és négyzetté alakitással),hogy ha x,y,z pozitivak

$\frac{a^2}{x}+\frac{b^2}{y} \geq \frac{(a+b)^2}{x+y}$

Innen pedig rögtön adódik több tagra is hogy pl.

$\frac{a^2}{x}+\frac{b^2}{y}+\frac{c^2}{z} \geq \frac{(a+b+c)^2}{x+y+z}$

A konkrét esetben pedig

$\frac{a}{2b+c}+\frac{b}{2c+a}+\frac{c}{2a+b}=\frac{a^2}{2ab+ac}+\frac{b^2}{2bc+ab}+\frac{c^2}{2ac+bc} \geq$

$\geq \frac{(a+b+c)^2}{2ab+ac+2bc+ab+2ac+bc} =\frac{(a+b+c)^2}{3(ab+bc+ca)}\geq 1$ ,ez pedig már nyilvánvaló.

A megoldás előnye hogy tetszőlegesen sok tagra általánositható pl.

$\frac{a}{2b+c+d+e}+\frac{b}{2c+d+e+a}+\frac{c}{2d+e+a+b}+\frac{d}{2e+a+b+c}+\frac{e}{2a+b+c+d} \geq 1$

Előzmény: [291] Csimby, 2005-09-05 21:25:00

[293] Csimby

2005-09-07 15:35:15

És akkor a folytatás (sajnos nem találtam egyszerűbbet mint felszorozni mindkét oldalt a bal oldalon lévő nevezőkkel):

a(2c+a)(2a+b)+b(2b+c)(2a+b)+c(2b+c)(2c+a) $\ge$ (2b+c)(2c+a)(2a+b)

2a³+a²b+4ab²+2b³+4a²c+6abc+b²c+ac²+4bc²+2c³ $\ge$ 4a²b+2ab²+2a²c+9abc+4b²c+4ac²+2bc²

2a³+2ab²+2b³+2a²c+2bc²+2c³ $\ge$ 3a²b+3abc+3b²c+3ac²

Számtani és mértani közép közti egyenlőtlenséggel könnyen bizonyítható, hogy:

ab²+a²c+bc² $\ge$ 3abc

A rendezési tétel miatt:

a³+b³+c³ $\ge$ a²b+b²c+ac²

Már csak ezt a 3 egyenlőtlenséget kell belátnunk:

a(a²+b²) $\ge$ 2a²b

b(b²+c²) $\ge$ 2b²c

c(c²+a²) $\ge$ 2ac²

Az első egyenlőtlenségben a-val, másodikban b-vel, harmadikban c-vel leosztva szintén a számtani és mértani középpel játszva bizonyítható állításokat kapunk.

A közepeket tényleg mindenütt alkalmaztuk, hiszen a,b és c is 2-2 négyzetszám összege, vagyis nem negatív.

Egyenlőség akkor lehet, amikor a közepekben és a rendezési tételben is egyenlőség van, vagyis ha a=b=c. Ekkor x²+y²=y²+z²=x²+z², vagyis x²=y²=z².

Előzmény: [291] Csimby, 2005-09-05 21:25:00

[292] Lóczi Lajos	2005-09-05 22:35:40
Vagy (gömbi koordináták helyett): a változószám úgy is csökkenthető, ha mindhárom törtet végigegyszerűsítjük pl. y²-tel: ekkor két új (hányadosokat tartalmazó) változóra átírható az egész. (Hátránya a gömbi koordinátákhoz képest, hogy a változók értelmezési tartományai a pozitív számok lesznek, tehát nem korlátos halmaz. Végigszámolva ebben a konkrét példában azonban egyszerűbb kétváltozós polinomhoz vezet ez a helyettesítés: a rezultánsegyenletnek csak 1 pozitív gyöke van.)
Előzmény: [290] Lóczi Lajos, 2005-09-01 16:23:34

[291] Csimby

2005-09-05 21:25:00

Szerintem így lehetne elindulni:

x²+y²=a, y²+z²=b és z²+x²=c helyettesítés után ezt kapjuk:

$\frac{a}{2b+c}+\frac{b}{2c+a}+\frac{c}{2a+b}>=1$

Előzmény: [289] Suhanc, 2005-08-29 09:37:23

[290] Lóczi Lajos

2005-09-01 16:23:34

Az alábbi, egy lehetséges megoldás nyilván nem a legrövidebb, de viszonylag általános eszközöket használ, ezért beírom.

Mivel csupa négyzetes tagok szerepelnek, az az ötletem támadt, hogy térbeli polárkoordinátákat (azaz gömbi koordinátákat) alkalmazzak:

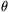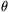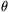x=r^.cos $\phi$ ^.cos $\theta$ , y=r^.sin $\phi$ ^.cos $\theta$ , z=r^.sin $\theta$ ,

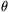ahol r>0 (r=0 nyilván nem lehet a nevezők miatt), $\phi$ $\in$ [0,2 $\pi$ ] a forgásszög, $\theta$ $\in$ [- $\pi$ /2, $\pi$ /2] pedig az emelkedési szög.

A bizonyítandó

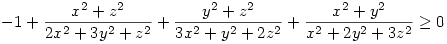
$-1 + \frac{x^2 + z^2}{2x^2 + 3y^2 + z^2} + \frac{y^2 + z^2}{3x^2 + y^2 + 2z^2} + \frac{x^2 + y^2}{x^2 + 2y^2 + 3z^2}\geq 0$

egyenlőtlenségben elvégezve ezeket a helyettesítéseket r kiesik, és csak két változónk marad!

A közös nevezőre hozás után kapunk egy törtet, aminek a nevezője három pozitív szám szorzata, elég tehát a számlálót nézni. Ez nem lesz más, mint

g(A,B):=3-11B+5AB+16B²-28AB²+13A²B²-5B³+12AB³+3A²B³-5A³B³,

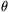ahol az A:=cos² $\phi$ , B:=cos² $\theta$ rövidítéseket használtam. (A szinuszokat a Pitagorasz-tétellel koszinuszokká konvertáltam.)

A továbbiakban elegendő tehát megmutatni, hogy g(A,B) $\ge$ 0 a [0,1]×[0,1] egységnégyzeten, és megnézni, hol állhat egyenlőség.

Most standard szélsőértékszámítást használtam. Könnyű ellenőrizni, hogy g(A,0), g(A,1), g(0,B) és g(1,B) valamennyien pozitívak, ha A,B $\in$ [0,1]. A peremen tehát stimmel a dolog, csak "belül" kell vizsgálódni.

Keressük meg a szokásos módon g lokális szélsőértékeit. Ez egy kis számolás. A derivált(vektor)nak kell megkeresni a zérushelyeit az egységnégyzeten belül (az alsó index jelöli a parciális deriválást): fenn kell álljon, hogy (*)

g_A(A,B)=5B-28B²+26AB²+12B³+6AB³-15A²B³=0

g_B(A,B)=-11+5A+32B-56AB+26A²B-15B²+36AB²+9A²B²-15A³B²=0

egyszerre nullák. Mivel egy (polinom)egyenletrendszernek csak ott lehetnek megoldásai, ahol a rezultáns nulla, vettem a fenti két egyenlet B-szerinti rezultánsát. Ez A-ban az alábbi ötödfokú egyenlet lett (rögtön faktorizálva egy kicsit):

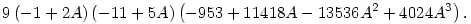
$9\left( -1 + 2A \right) \left( -11 + 5A \right) \left( -953 + 11418A - 13536A^2 + 4024A^3 \right).$

Ennek a gyökei között vannak a lehetséges A-értékek, amelyek (*) megoldásait adják. Nem nehéz kiszűrni, hogy a fenti egyenletnek [0,1]-ben csak A=1/2-nél van gyöke, illetve van még egy gyök az A $\in$ [9/100,1/10] intervallumban is. Zárjuk ki ez utóbbit.

Elemien meggondolható, hogy a B $\to$ g_B(A,B) függvény monoton nő [0,1]-en tetszőleges A $\in$ [9/100,1/10] esetén. Mivel azonban g(A,4/10) minden A $\in$ [9/100,1/10] esetén negatív, ezért g_B(A,B)<0, ha A $\in$ [9/100,1/10] és B $\in$ [0,4/10]. A másik egyenletről hasonlóan bebizonyítható, hogy g_A(A,B)<0, ha A $\in$ [9/100,1/10] és B $\in$ [4/10,1]. Ezekből az következik, hogy a (*) egyenletRENDSZERnek nincs megoldása, ha A $\in$ [9/100,1/10] és B $\in$ [0,1].

Marad tehát az A=1/2 egyetlen lehetséges megoldása (*)-nak. Ez pedig valóban jó, amint azt B=2/3 mutatja.

Ott tartunk, hogy az egységnégyzet belsejében a g kétváltozós függvénynek csak (A,B)=(1/2,2/3)-nál LEHET szélsőértéke. A szokásos, Hesse-mátrixos másodrendű elégséges feltétellel azonban meggyőződhetünk róla, hogy itt valóban szélsőérték is VAN, mégpedig lokális minimum.

Meglepő, hogy ez éppen zérushely is: g(1/2,2/3)=0.

A feladat eredeti állítását tehát bebizonyítottuk, és ebből az egyenlőség esete is könnyen látható: a megadott A és B értékekből a 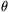$\phi$ és $\theta$ szögek visszaszámolhatók. Ezekből az eredeti x,y és z változókra azt kapjuk, hogy x= $\pm$ y (hiszen cos²( $\pi$ /4)=sin²( $\pi$ /4)=1/2), sőt, azt is, hogy x= $\pm$ z (y előjelétől függetlenül), ami pedig azon múlik, hogy

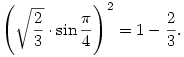
$\left(\sqrt{\frac{2}{3}}\cdot \sin\frac{\pi}{4}\right)^2=1-\frac{2}{3}.$

Egyenlőség az eredeti feladatban pontosan akkor van tehát, ha |x|=|y|=|z|.

Előzmény: [289] Suhanc, 2005-08-29 09:37:23

[289] Suhanc

2005-08-29 09:37:23

72.Feladat:

Bizonyítsuk be a megadott egyenlőtlenséget, és vizsgáljuk meg, teljesülhet-e egyenlőség esete!

$\frac{x^2+y^2}{3z^2+2y^2+x^2} +\frac{y^2+z^2}{3x^2+2z^2+y^2}+ \frac{z^2+x^2}{3y^2+2x^2+z^2} \ge 1$

[288] Suhanc	2005-08-29 09:17:54
...általánosan talán annyit mondhatunk, minden olyan évszámra kizárólag Jonas elképzelése müködőképes, ha a fent leírt szabálynak (evszam-n=j(n)) csak 1 megoldása van, míg, a (evszam-1-n= j(n))-nek legalább egy megoldása van...
Előzmény: [287] Suhanc, 2005-08-29 09:13:04

[287] Suhanc

2005-08-29 09:13:04

Kedves László!

Őszintén szólva Jonas észrevétele után bennem ez a feladat kissé fogásmentessé vált. A konkrét kérdésedre válaszolva, a 2005 szerintem is csak Jonas verziójában működik. Nézzük meg egyenlőre azokat a számokat, melyekre, ha j(n) a szj-ek összege,

2005-n=j(n)

Majd ugyanezt tegyük meg 2004- re is! 2005-re egyetlen példát talált (a gép...:D), amennyiben feltételezzük, hogy 1000 előtt születettek ma már nem élnek. Ez az 1979. Míg 2004-re megfelel 1983 és 2001. Miért kerestünk 2004-re is? Mert az elsőnek elképzelt verzió szerint a feladatnak nem lehet megoldása, hisz egyetlen lehetséges megoldásunk nem lehet azapa és a fiú születési ideje. Ezáltal látszik meg a másik értelmezés pontosító hatása:

Tegyük fel, hogy az év olyan szakaszában vagyunk, amikor a két családtag közül pontosan egyik ünnepelte a születésnapját. (ha még egyik sem ünnepelte, azt nyugodtan tekinthetjük az előző évnek)

Ekkor egyiküknél a 2005-ös képletet kell használnunk, míg a másiknál a 2004-est, hisz ugyanolyan idős, mint 2004-ben, makor betöltötte. Ez alapján már kreálhautnk számpárokat.

Lehetséges pl. hogy az apa 1979-es születésű, míg a fiú 1983 (!!!), avagy az apa 1979,a fiú 2001. Mindkét esetben az apa ünnepelte már a születsnapját.

Előzmény: [285] lorantfy, 2005-07-27 15:37:14

[286] [evilcman]

2005-08-23 18:53:03

71.

p=2 igaz, máskor

* (3;p)=1; (2;p)=1; (6;p)=1

a kis Fermat tételből:

2^p-1=pa+1

3^p-1=pb+1

6^p-1=pc+1

a vizsgált kifejezés így : (3pa + 2pb + pc)/6 egész szám, ugyanakkor * ( (3a + 2b + c)/6 is egész )

Előzmény: [284] Ali, 2005-07-25 09:25:38

[285] lorantfy

2005-07-27 15:37:14

Szia Suhanc!

Kösz, hogy foglalkoztál a feladattal! Gondold át, ha van kedved hozzá, hogy milyen évszámmal kellene megadni a feladatot, hogy csak a Jónás féle verzióban legyen megoldás! (Lehet, hogy 2005 jó lenne?)

Persze más is elgondolkodhat rajta!

Előzmény: [282] Suhanc, 2005-07-12 22:06:32

[284] Ali

2005-07-25 09:25:38

71. feladat.

Ha p $\ne$ 3 prím, akkor 2^p-2 + 3^p-2 + 6^p-2 - 1 osztható p -vel.

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?