Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[428] Gubbubu

2005-11-09 13:46:47

Egy tényleg egyszerűke kis feladat, kisebbeknek (a "szultán és rabok" néven is ismert fa. egy variációja):

Gilgames, Uruk város pateszije (uralkodója), a Legyőzhetetlen Bika, Az Istenek Ereje, Istár Istenasszony Kegyeltje, Győzedelmes Minden Égtájak Seregei Fölött, Kedves Az Égiek Előtt. etc. etc. trónra kerülése után az ilyen alkalmakkor szokásos közkegyelemben részesíti a Borzalmak Háza (az uruki börtön) nyomorult lakóit. Megbízza száz hű emberét, hogy az első mindegyik ajtót nyissa ki, a második minden másodikat zárja be, a harmadik minden harmadikat nyissson ki, a negyedik minden negyediket zárja be ... és így tovább. Mely sorszámú cellák rabjai szabadulnak?

[427] Lóczi Lajos	2005-11-09 11:26:20
Jó, nyilván arra vonatkozott a kérdés, hogy minél kisebb apparátussal hogyan bizonyítható az állítás; vagy hol nézhet utána az érdeklődő az idézett tételnek :)
Előzmény: [426] ágica, 2005-11-09 06:18:00

[426] ágica	2005-11-09 06:18:00
Én úgy tudom, hogy egy szám lánctört közelítései konvergálnak az adott számhoz, tehát ezt nem kell bizonyítani :) A -1-nek pedig az 1/n sorozat nem a lánctört-közelítéseinek a sorozata :)
Előzmény: [423] Lóczi Lajos, 2005-11-08 23:04:28

[425] Lóczi Lajos	2005-11-09 02:28:48
Micsoda kacifántos megoldások születtek :-) (Én csak szimpla monotonitási érveléssel csináltam az egészet.)
Előzmény: [424] Róbert Gida, 2005-11-09 00:32:00

[424] Róbert Gida

2005-11-09 00:32:00

Ez a 80. feladat elég közismert a diofantikus approximáció elméletben, de azért van elemi megoldása is: Nézzük az 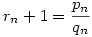$r_n+1=\frac {p_n}{q_n}$ sorozatot, ahol lnko(p_n,q_n)=1, ekkor a sorozatból pl. p₁=3;q₁=2 teljesül. Ekkor a rekurzióból:

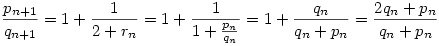
$\frac {p_{n+1}}{q_{n+1}}= 1+\frac 1{2+r_n}=1+\frac {1}{1+\frac {p_n}{q_n}}=1+\frac {q_n}{q_n+p_n}=\frac {2 q_n+p_n}{q_n+p_n}$

. De mivel lnko(p_n,q_n)=1 ezért itt a nevező és a számláló relatív prímek, azaz p_n+1=2q_n+p_n és q_n+1=q_n+p_n. Teljes indukcióval könnyen bizonyítható, hogy:

p_n²=2*q_n²+(-1)ⁿ⁺¹

teljesül. Ebből az egyenletből:

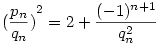
${(\frac {p_n}{q_n})}^2=2+\frac {(-1)^{n+1}}{q_n^2}$

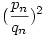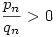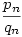. Mivel a rekurzióból q_n szigorúan monoton nő, ezért $(\frac {p_n}{q_n})^2$ tart 2-höz, de nyilván $\frac {p_n}{q_n}>0$ ezért $\frac {p_n}{q_n}$ tart $\sqrt 2$ -höz, azaz az eredeti sorozat $\sqrt 2-1$ -hez.

[423] Lóczi Lajos	2005-11-08 23:04:28
Körmönfont :) De azt az állítást, miszerint "n növekedésével az n-edik lánctört közelítés egyre jobban megközelíti $\alpha$ -t" hogy lehet bizonyítani? (Ráadásul az, hogy "egyre jobban megközelíti", nem feltétlenül jelenti azt, hogy a limesze is az lenne: pl. -1-et az 1/n sorozat egyre jobban megközelíti...)
Előzmény: [422] ágica, 2005-11-08 21:56:41

[422] ágica

2005-11-08 21:56:41

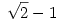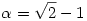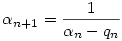80. megoldás: A sorozat első pár tagját kiszámolva adódhat az a sejtés, hogy a keresett határérték $\sqrt{2}-1$ . Ennek bizonyításához határozzuk meg az $\alpha=\sqrt{2}-1$ valós szám lánctört közelítéseit. Általánosan, ha $\alpha$ irracionális, $\alpha$ ₁= $\alpha$ , és n $\ge$ 1 esetén $\alpha_{n+1}=\frac{1}{\alpha_{n}-q_{n}}$ , ahol q_n egyenlő $\alpha$ _n alsó egész részével, akkor $\alpha$ n-edik lánctört közelítése:

$\delta_n=//q_1,...,q_n//=q_1+\frac{1}{q_2+\frac{1}{q_3+\frac{1}{...+\frac{1}{q_n}}}}$ .

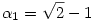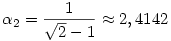Ebben az esetben tehát $\alpha_{1}=\sqrt{2}-1$ , q₁=0, $\alpha_{2}=\frac{1}{\sqrt{2}-1}\approx{2,4142}$ , q₂=2.

$\alpha$ ₃-at kiszámolva azt kapjuk, hogy megegyezik $\alpha$ ₂-vel, tehát q₃=q₂, így a képzési szabály miatt minden n $\ge$ 2-re $\alpha_{n}=\frac{1}{\sqrt{2}-1}$ és q_n=2. Vagyis

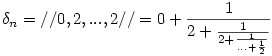$\delta_n=//0,2,...,2//=0+\frac{1}{2+\frac{1}{2+\frac{1}{...+\frac{1}{2}}}}$ ,

ami nem más, mint az r sorozat n-1-edik tagja. n növekedésével az n-edik lánctört közelítés egyre jobban megközelíti $\alpha$ -t, ami azt jelenti, hogy

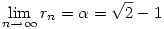$\lim_{n\to\infty}r_{n}=\alpha=\sqrt{2}-1$ .

Előzmény: [398] Lóczi Lajos, 2005-10-30 21:17:15

[421] Lóczi Lajos	2005-11-06 16:34:32
Szép ötletek és kivitelezés, jó volt olvasni! Azt gondolom, a feladatot ezzel eléggé kiveséztük :)
Előzmény: [420] Róbert Gida, 2005-11-06 12:12:51

[420] Róbert Gida

2005-11-06 12:12:51

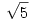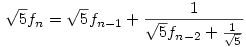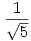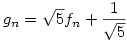81.b feladatra, a sorozatra még egy élesebb egyenlőtlenség is kijött, mint amit a limeszes becslés adna. Eltüntetem először a konstansokat a rekurzióból; szorozzuk a rekurziót $\sqrt 5$ -tel, ekkor: $\sqrt 5f_n=\sqrt 5f_{n-1}+\frac 1{\sqrt 5f_{n-2}+\frac 1{\sqrt 5}}$ Adjunk mindkét oldalhoz $\frac1{\sqrt 5}$ -öt és legyen az új sorozat $g_n=\sqrt 5f_n+\frac 1{\sqrt 5}$ ; ekkor

$g_n=g_{n-1}+\frac 1{g_{n-2}}$

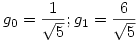
, ha n>1 és $g_0=\frac 1{\sqrt 5}; g_1=\frac 6{\sqrt 5}$

Ez a rekurzió, ha a nevezőben g_n-1 lenne, akkor pont az 1975. évi 3. Kürschák példa rekurziója volna! Az ottani ötlettel: emeljük négyzetre a rekurziót, kapjuk:

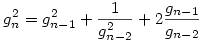
$g^2_n=g^2_{n-1}+\frac 1{g^2_{n-2}}+2\frac{g_{n-1}}{g_{n-2}}$

Adjuk össze ezeket az egyenleteket 2-től n-ig, sok tag kiesik, kapjuk:

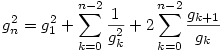$g^2_n=g^2_1+\sum_{k=0}^{n-2}\frac 1{g^2_k}+ 2\sum_{k=0}^{n-2}\frac {g_{k+1}}{g_k}$

(1)

De g₁>g₀ és a rekurzióból g monoton nő; így a második szumma minden tagja legalább egy:

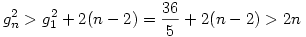
$g^2_n>g^2_1+2(n-2)=\frac {36}{5}+2(n-2)>2n$

de ez n=0;1-re is teljesül és g tagjai pozitivak, így

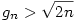
$g_n>\sqrt {2n}$

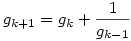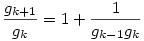teljesül. Pont ebből az alsó becslésből kapjuk a felső becslést. g sorozatra vonatkozó rekurziót k+1-re felírva: $g_{k+1}=g_k+\frac 1{g_{k-1}}$ , ezt g_k-val osztva: $\frac {g_{k+1}}{g_k}=1+\frac 1{g_{k-1}g_k}$ , ha k>0. Így az (1) egyenletből:

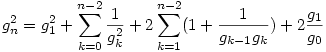
$g^2_n=g^2_1+\sum _{k=0}^{n-2} \frac 1{g^2_k}+2\sum _{k=1}^{n-2} (1+\frac 1{g_{k-1}g_k})+ 2\frac {g_1}{g_0}$

, azaz

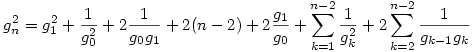
$g^2_n=g^2_1+\frac 1{g^2_0}+2\frac 1{g_0g_1}+2(n-2)+2\frac {g_1}{g_0}+\sum _{k=1}^{n-2} \frac 1{g^2_k}+2\sum _{k=2}^{n-2} \frac 1{g_{k-1}g_k}$

, g monotonitását és g₀,g₁ értékét használva kapjuk:

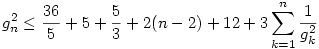
$g^2_n\leq \frac {36}5+5+\frac 53+2(n-2)+12+3\sum _{k=1}^n \frac 1{g^2_k}$

, de 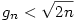$g_n<\sqrt {2n}$ , így

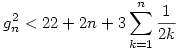
$g^2_n<22+ 2n+3\sum _{k=1}^n \frac 1{2k}$

, ismert, hogy 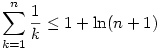$\sum _{k=1}^n \frac 1k\leq 1+\ln (n+1)$ , ha n $\geq$ 0, így

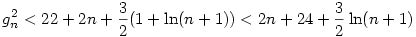
$g^2_n<22+2n+\frac 32(1+\ln (n+1))<2n+24+\frac 32 \ln (n+1)$

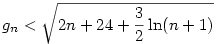, azaz $g_n<\sqrt {2n+24+\frac 32 \ln (n+1)}$ , de ez n=0;1-re is teljesül, így minden n-re igaz. Visszaírva g definicióját és az alsó becslést is használva, kapjuk:

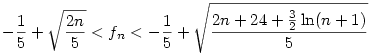
$-\frac 15+\sqrt {\frac {2n}{5}}<f_n<-\frac 15+ \sqrt {\frac {2n+24+\frac 32 \ln (n+1)}{5}}$

Amiből már látszik a bizonyítandó, sőt ez élesebb becslés is annál.

[419] Lóczi Lajos

2005-11-05 23:00:13

Egy kis heurisztika:

átrendezve a rekurzív egyenletet kapjuk, hogy 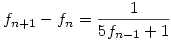$f_{n+1}-f_{n}=\frac{1}{5 f_{n-1}+1}$ . Fogjuk fel f-et folytonos függvényként. Ekkor a bal oldal körülbelül f '(n), és (némi további elhanyagolással) a következő differenciálegyenletet nyerjük:

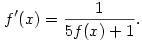
$f'(x)=\frac{1}{5f(x)+1}.$

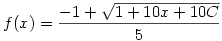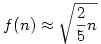Ezt viszont expliciten meg tudjuk oldani, azt kapjuk, hogy $f(x)=\frac{-1 + {\sqrt{1 + 10x + 10C}}}{5}$ , azaz nagy n-ekre $f(n)\approx \sqrt{\frac{2}{5}n}$ .

Előzmény: [418] nadorp, 2005-11-05 13:41:09

[418] nadorp

2005-11-05 13:41:09

Mondjuk,ez már nem ujjgyakorlat, de hátha valaki foglalkozik vele:

81.b feladat: Bizonyítsuk be, hogy $\lim_{n\to\infty}\frac{f_n}{\sqrt{n}}=\sqrt{\frac25}$

Előzmény: [399] Lóczi Lajos, 2005-10-30 21:19:45

[417] jenei.attila

2005-11-01 23:39:18

Lényegét tekintve Káli gúla megoldása nagyon hasonló az enyémhez, persze némileg egyszerűbb. Tehát az

$y:=x-\frac{5x}{x+5}$

helyettesítés a legmegfelelőbb.

Előzmény: [414] lorantfy, 2005-11-01 21:01:10

[416] lorantfy

2005-11-01 22:27:25

Hát persze, hogy be szabad írni, sőt kötelező, annak aki tudja! :-)

Nyilván van többféle megoldása, de létezik egy olyan is aminek köze van a sakkhoz.

Előzmény: [415] Lóczi Lajos, 2005-11-01 21:50:07

[415] Lóczi Lajos	2005-11-01 21:50:07
Be szabad írni a megoldást? :) Csak nem valahogy a sakkhoz van köze a feladatnak?
Előzmény: [414] lorantfy, 2005-11-01 21:01:10

[414] lorantfy

2005-11-01 21:01:10

Kedves Káli gúla!

Ötletes és egyszerű megoldás. Köszönöm! Az enyém túl körülményes.

Felhívom a figyelmedet a 202. feladatra az Érdmatfelben. Egy barátomtól hallottam, aki remélhetőleg hamarosan sakkmester lesz!

Előzmény: [413] Káli gúla, 2005-11-01 20:15:01

[413] Káli gúla

2005-11-01 20:15:01

Kedves László!

Az 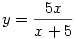$y=\frac{5x}{x+5}$ jelöléssel az egyenlet x²+y²=11 alakú. A helyettesítésből (*) xy=5(x-y), ezért

x²+y²=(x-y)²+2xy=(x-y)²+10(x-y)=11.

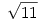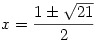A $\sqrt{11}$ sugarú kör a (*) hiperbolának csak a jobb oldali ágát metszi, ahol y $\le$ x, így az 1 és a -11 közül csak az x-y=1 gyök jó. Ezt visszaírva (*)-ba az x(x-1)=5 egyenletet kapjuk, aminek a gyökei $x=\frac{1\pm \sqrt{21}}2$ .

Előzmény: [409] lorantfy, 2005-10-31 13:56:12

[412] Lóczi Lajos	2005-10-31 22:27:10
(Pontosítok: amit a legutolsó mondatban írtál, annak nincs köze a limesz definíciójához; az csak annyit jelent, hogy a $\sqrt{2}-1$ torlódási pontja a sorozatnak.)
Előzmény: [406] Suhanc, 2005-10-31 10:30:45

[411] Lóczi Lajos	2005-10-31 17:47:59
Amit írtál az annyit mond: ha feltesszük, hogy a határérték létezik, akkor az értéke csak 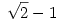$\sqrt{2}-1$ lehet. (Tehát a limesz létét is meg kellene mutatni, de nem muszáj a definíció alapján, ahogyan írtad, egyszerűbb hivatkozni olyan állításokra, mint pl. "ha egy sorozat monoton és korlátos, akkor konvergens" -- ilyesmit kell keresni pl.)
Előzmény: [406] Suhanc, 2005-10-31 10:30:45

[410] Lóczi Lajos	2005-10-31 17:40:43
De attól még a válaszom a 83. feladatra ugyanaz: lásd a [394]-es hozzászólást.
Előzmény: [405] Edgar, 2005-10-31 07:39:29

[409] lorantfy

2005-10-31 13:56:12

Kedves Attila!

Kösz a szép megoldást! Beírom az én megoldásomat is.

76. megoldása helyettesítéssel:

$x^2+\frac{25x^2}{(x+5)^2}=11$

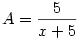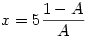$\frac{25x^2}{(x+5)^2}=25 \big(\frac{x+5-5}{x+5}\big)^2= 25 \big(1-\frac{5}{x+5}\big)^2$ itt legyen $A=\frac{5}{x+5}$ ebből $x=5\frac{1-A}{A}$ ezt visszaírva az eredeti egyenletbe:

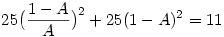
$25 \big (\frac{1-A}{A}\big )^2 +25 (1-A)^2=11$

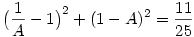
$\big (\frac{1}{A}-1\big )^2 +(1-A)^2=\frac{11}{25}$

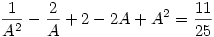
$\frac{1}{A^2}-\frac{2}{A}+2-2A+A^2=\frac{11}{25}$

$\big (A+\frac{1}{A}\big)^2-2\big (A +\frac{1}{A})-\frac{11}{25}=0$

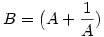
$B=\big (A +\frac{1}{A})$

25B²-50B-11=0

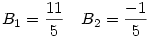
$B_1=\frac{11}{5} \quad B_2=\frac{-1}{5}$

Az első gyök ad valós megoldást A-ra:

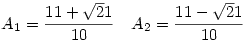
$A_1=\frac{11+\sqrt21}{10}\quad A_2=\frac{11-\sqrt21}{10}$

Ezt visszahelyettesítve:

$x_1=\frac{1-\sqrt21}{2}\quad x_2=\frac{1+\sqrt21}{2}$

Előzmény: [407] jenei.attila, 2005-10-31 11:58:40

[408] jenei.attila	2005-10-31 12:23:36
Közvetlenebb helyettesítéssel: $y:=\frac{-5x}{x+5}$ , amiből látszik, ha x gyök, akkor y is az.
Előzmény: [407] jenei.attila, 2005-10-31 11:58:40

[407] jenei.attila

2005-10-31 11:58:40

Végezzük el az y:=-x és

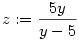
$z:=\frac{5y}{y-5}$

helyettesítést. Ezzel az eredeti egyenlet

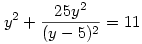
$y^2+\frac{25y^2}{(y-5)^2}=11$

, illetve

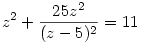
$z^2+\frac{25z^2}{(z-5)^2}=11$

alakú lesz. Vagyis, ha y gyöke az egyenletnek, akkor z is az. De

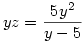
$yz=\frac{5y^2}{y-5}$

és

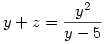
$y+z=\frac{y^2}{y-5}$

. Ezért a másodfokú egyenlet gyökeinek és együtthatóinak összefüggése szerint y és z egy x²+px-5p=0 alakú egyenelet gyökei, míg az eredeti egyenletből kapott negyedfokú egyenlet 3. és 4. gyöke szintén a x²+qx-5q=0 alakú egyenlet gyökei. Elvégezve a két másodfokú egyenlet összeszorzását és az együtthatók összehasonlítását p=1, q=-11 -et kapunk, amiből az eredeti gyökök könnyen megkaphatók.

Előzmény: [382] lorantfy, 2005-10-29 11:54:41

[406] Suhanc

2005-10-31 10:30:45

Próba-szerencse:

Legyen 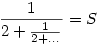$\frac{1}{2+\frac{1}{2+...}}=S$ !

Ekkor nyilván 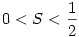$0<S<\frac{1}{2}$ Tehát ezen intervallumon keressük S értékét!

Fenti egyenletünk reciprokát véve:

$2+ \frac{1}{2+\frac{1}{2+...}}= \frac{1}{S}$

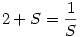
Azaz: $2+S= \frac{1}{S}$

Amiből: S²+2S-1=0

Itt S értékére két lehetőség van, ebből fenti kikötéseinket 1teljesíti: 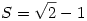$S=\sqrt2 -1$

Ez elfogadható S keresés? Avagy szükséges, hogy minden $\varepsilon$ -ra mutassuk a_n-t. amire 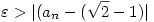$\varepsilon> |(a_n-(\sqrt2 -1)|$ ?

Előzmény: [398] Lóczi Lajos, 2005-10-30 21:17:15

[405] Edgar

2005-10-31 07:39:29

jajajj, feladatom törvényen kívül került, mert nem adtam néki számot :-( Legyen:

83. feladat: Oldd meg a természetes számok körében:

x⁵-y²=4

Előzmény: [393] Edgar, 2005-10-30 19:32:45

[404] Róbert Gida	2005-10-30 23:32:26
A probléma nekem is megtetszett: valóban a Maple 9.5 sem tudja egyszerűsíteni a simplify paranccsal a formulát, ezután megpróbáltam a Mathematica 5.1-gyel, hogy mit tud: az egyszerübb Simplify itt sem egyszerűsít, de a bonyolultabb FullSimplify paranccsal 0.75 másodperc alatt megmondja, hogy az érték 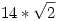$14*\sqrt 2$ . Csodálatos, hogy már ilyen computeralgebra rendszer is van.
Előzmény: [392] Edgar, 2005-10-30 19:21:55

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?