Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[603] jenei.attila	2010-02-23 08:16:10
Persze hogy megadható, mégpedig úgy, hogy kiszámoljuk az a,b,x,y-t. De ha ez a rekurzió neked nem jött ki, akkor másképp oldottad meg a feladatot. Szerintem most már beszéljük meg a megoldásokat.
Előzmény: [602] R.R King, 2010-02-22 20:40:19

[602] R.R King	2010-02-22 20:40:19
Bár magam nem számoltam utána, de ha ez így van, akkor cn megadható n függvényében is. Nem rossz ez a feladat.
Előzmény: [601] jenei.attila, 2010-02-22 17:22:26

[601] jenei.attila	2010-02-22 17:22:26
Valóban, ha c_n-nel jelöljük axⁿ+byⁿ-et, akkor c_n+2=38c_n-14c_n+1
Előzmény: [600] R.R King, 2010-02-22 16:21:51

[600] R.R King	2010-02-22 16:21:51
Igen, a 20 az jó lesz. Sőt, szerintem sorozatok segítségével 5 helyett n kitevőre is célhoz érhetünk..
Előzmény: [599] m2mm, 2010-02-22 14:40:07

[599] m2mm	2010-02-22 14:40:07
Igen:)
Előzmény: [598] jenei.attila, 2010-02-22 14:25:52

[598] jenei.attila	2010-02-22 14:25:52
20?
Előzmény: [597] m2mm, 2010-02-18 21:06:12

[597] m2mm

2010-02-18 21:06:12

Az idei Arany Dani haladó/3.kategória 3. feladata: Az a,b,x,y valósokra ax+by=3, ax²+by²=7, ax³+by³=16 és ax⁴+by⁴=42. Mennyi ax⁵+by⁵?

Aki ismeri, hogyan kell megoldani, az ne lője le.

[596] Fernando	2010-02-07 10:39:42
Köszönöm, tanulmányozom!
Előzmény: [594] Lóczi Lajos, 2010-02-05 21:07:12

[595] Fernando

2010-02-07 10:38:59

Köszi!

Egyelőre próbálom "kitakarni", hogy ne lássam a gondolatmenetedet.

Előzmény: [593] jonas, 2010-02-05 21:03:59

[594] Lóczi Lajos	2010-02-05 21:07:12
Ezen a linken sok hivatkozást találsz a válaszhoz.
Előzmény: [592] Fernando, 2010-02-05 20:20:08

[593] jonas

2010-02-05 21:03:59

Tetszőleges pozitív valós szám előáll, és ezt nem is nehéz bizonyítani. Ha gondolod, próbáld meg belátni, mielőtt az alábbit elolvasod, mert hasznos gyakorlat.

Annyit elég kihasználni a sorozatról, hogy az összege végtelen, de a tagjai pozitívak és nullához tartanak.

Egyszerűen sorba mész a számokon, és akkor veszel be egy számot az összegbe, ha ezzel az eddigi részletösszeg nem éri el a keresett x számot. Mivel a kiválasztott számok részletösszegei monoton nőnek, és nem haladják meg x-et, a sor konvergens, és az összege legfeljebb x. Másrészt vegyük észre, hogy nem választhattuk be véges sok kivételével minden tagot az ereddeti sorozatból, mert akkor az összeg végtelen lenne. Ha mármost az összeg x-nél kisebb lenne, mondjuk y, akkor minden részletösszeg is legfeljebb y; csakhogy mivel az eredeti sorozat nullához tart, ezért véges sok kivételével minden tagja kisebb x-y-nál, ezért ezekből mindet be kellett volna választani a szabály szerint, ami ellentmondás az előzővel.

Előzmény: [592] Fernando, 2010-02-05 20:20:08

[592] Fernando

2010-02-05 20:20:08

Ma egy elméleti fizikus cimborámmal ebédeltem és fölmerült ennek a eredményeképpen fölmerült a következő kérdés:

Tekintsük a természetes számok reciprokaiból álló sorozatot.

A tagok közül tetszőleges mennyiségűt (akár végtelen sokat is) összeadva összegként előáll-e tetszőleges valós szám? (erősen sejtjük, hogy igen)

Ha igen, akkor pl. a pí-t hogyan lehet előállítani? (ez utóbbi lehet, hogy nagyon nehéz)

[591] nadorp

2010-02-04 20:42:56

Ez nem az én napom, de mindegy, tehát újra javítom az elírásokat

$\int_{k\pi}^{(k+1)\pi}\frac{\sin^2}xdx>\int_{k\pi+\frac\pi4}^{k\pi+\frac{3\pi}4}\frac{\sin^2}xdx\geq\int_{k\pi+\frac\pi4}^{k\pi+\frac{3\pi}4}\frac{\left(\frac1{\sqrt2}\right)^2}{k\pi+\frac{3\pi}4}=\frac1{4k+3}>\frac14\cdot\frac1{k+1}$

A többi már értelemszerűen adódik :-)

Előzmény: [589] nadorp, 2010-02-04 19:52:23

[590] nadorp

2010-02-04 19:56:51

Bocs, a vége helyesen

$\int_0^{(n+1)\pi}...$

Előzmény: [589] nadorp, 2010-02-04 19:52:23

[589] nadorp

2010-02-04 19:52:23

Lelövöm, ha nincs rá jelentkező.

$\int_0^\infty\frac{\sin^2x}xdx$ végtelen, mert

$\int_{k\pi}^{(k+1)\pi}\frac{\sin^2x}xdx>\int_{k\pi+\frac\pi4}^{(k+1)\pi+\frac{3\pi}4}\frac{\sin^2x}xdx\geq\int_{k\pi+\frac\pi4}^{(k+1)\pi+\frac{3\pi}4}\frac{\left(\frac1{\sqrt2}\right)^2}{(k+1)\pi+\frac{3\pi}4}=\frac1{4k+7}>\frac14\cdot\frac1{k+2}$

$\int_0^{n\pi}\frac{\sin^2x}xdx>\frac14\sum_{k=0}^n\frac1{k+2}$

Előzmény: [566] Lóczi Lajos, 2009-10-13 01:37:52

[588] vogel

2010-02-03 16:01:01

Úgy látom, mindenki félreértett. :-) Amit én beírtam, azt azelőtt kezdtem el írni, hogy nadorp is beírta, így nem nadorp-nek címeztem, bocs.

Az összeadást arra értettem, hogy ha szorzás helyett összeadás lenne: y'+y=2x+y, ami azért vicces. :-)

Előzmény: [586] nadorp, 2010-02-03 15:30:55

[587] Fernando	2010-02-03 15:40:20
Nadorp implicit megoldását átnéztem, ok, értem is, tetszik!
Előzmény: [581] nadorp, 2010-02-03 15:05:58

[586] nadorp

2010-02-03 15:30:55

Nem látod a fától az erdőt :-), ugyanaz jött ki Neked is, ui

$\frac1{\frac2t-t+1}=\frac{-t}{t^2-t-2}$

Előzmény: [582] vogel, 2010-02-03 15:09:16

[585] Fernando

2010-02-03 15:30:39

Kedves Vogel!

Az összeadást nem a helyettesítésre mondtam. Egyébként kipróbáltam t=x/y és t=y/x -et is. Továbbá megkaptam azt amit itt írsz, de onnan azért t-t kihozni...

Előzmény: [582] vogel, 2010-02-03 15:09:16

[584] nadorp

2010-02-03 15:25:05

y^'y=2x+y

$y^{'}=\frac{2x+y}y=\frac{2+\frac yx}{\frac yx}$

$\frac yx=z$

y=zx

stb.

Előzmény: [582] vogel, 2010-02-03 15:09:16

[583] Fernando

2010-02-03 15:20:55

Kedves Jonas!

y'y=2x+y ez szerepel a feladatban! Tehát erről az egyenletről van szó!

(Más kérdés, hogy azt sejtem, hogy ez elírással keletkezett, mert levelezős mezőgazdasági gépész hallgatók feladatsorában volt kapásból az első feladat és az összes többi lényegesen egyszerűbb volt.)

Előzmény: [580] jonas, 2010-02-03 14:54:27

[582] vogel

2010-02-03 15:09:16

Összeadással vicces lenne. :-) Nem lehet, hogy helyettesítésnél véletlenül x/y-t helyettesítettél?

Mert ahogy írtam, abból ez jön: 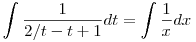$\int{\frac{1}{2/t-t+1}}dt=\int{\frac{1}{x}}dx$

[581] nadorp

2010-02-03 15:05:58

Ha nem akarod explicit módon megadni y-t akkor a megoldás szépnek is nevezhető ( hacsak el nem számoltam ) A SmallPotato által talált "rondaság" amiatt van, mert egy harmadfokú egyenletet kell megoldani, valószínűleg casus irreducibilis esetben. Ráadásul az ott szereplő képlet is kapásból egyszerűsithező az e^3C₁=C helyettesítéssel, de hát azt a mgeoldást egy program adta, nem lehet belekötni

A y=zx helyettesítéssel ( ahogy Vogel is ajánlotta)

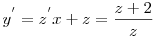
$y^{'}=z^{'}x+z=\frac{z+2}z$

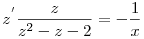
$z^{'}\frac{z}{z^2-z-2}=-\frac1x$

$z^{'}\frac13\left(\frac2{z-2}+\frac1{z+1}\right)=-\frac1x$

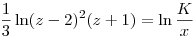
$\frac13\ln(z-2)^2(z+1)=\ln\frac Kx$

(y-2x)²(y+x)=K³=C

Előzmény: [578] Fernando, 2010-02-03 14:35:40

[580] jonas	2010-02-03 14:54:27
Nem értem, mi lenne akkor a helyes egyenlet szerinted?
Előzmény: [579] Fernando, 2010-02-03 14:46:28

[579] Fernando

2010-02-03 14:46:28

Kedves SmallPotato!

Ez tényleg elég durva, egyetértünk :) Amúgy azt sejtem, hogy elírás és szorzást akartak írni összeadás helyett...így viszont érdekesebb! "Szoktatom magam" hozzá kicsit! Lehet, hogy kijön talán-talán belőle a -X és a 2X. :)

Előzmény: [576] SmallPotato, 2010-02-03 14:10:54

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?