Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[708] logarlécész

2012-05-16 11:05:44

Ha jól értem, a megoldás kellene.

A legegyszerűbb grafikusan. A felrajzolásból látszik, hogy megoldás lesz a +2; -2 és lesz még egy megoldás -3 és -2 között. Ennek a pontos értékét én sem tudom meghatározni, nagyjából -2,19258, ha nem tévedek.

Előzmény: [707] juantheron, 2012-05-16 10:10:27

[707] juantheron

2012-05-16 10:10:27

how can i found real value of

x in $x^2 = 4+ \left[x\right]$

[706] juantheron	2012-05-16 10:05:55
$\int \frac{1}{\sin^3 x+\cos^3 x}dx$

[705] Róbert Gida	2012-05-15 21:02:33
Mathematica szerint: $y=\frac {x^2+2x-1}{4}$
Előzmény: [704] Lóczi Lajos, 2012-05-15 20:21:56

[704] Lóczi Lajos

2012-05-15 20:21:56

Fejezzük ki valamelyik változót a másik segítségével az

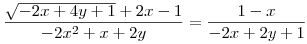
$\frac{\sqrt{-2 x+4 y+1}+2 x-1}{-2 x^2+x+2 y}=\frac{1-x}{-2 x+2 y+1}$

egyenletből.

[703] nadorp

2012-01-10 13:35:16

Egy "kis számolás" után (deriválás,visszaintegrálás) rá lehet jönni, hogy ha

$f(x)=\sum_{n=0}^{\frac{p-1}2}(-1)^n\binom{2n}{n}x^n$ , akkor (1+4x)f(x)=q(x) (mod p)

Előzmény: [702] Maga Péter, 2011-12-31 08:29:37

[702] Maga Péter	2011-12-31 08:29:37
Szép kis ujjgyakorlat... :P
Előzmény: [701] Kemény Legény, 2011-12-29 01:30:08

[701] Kemény Legény

2011-12-29 01:30:08

Erről a maradékosztályos témáról eszembe jutott egy viszonylag nehéz feladat (nem saját). Azt hiszem, a fórumon még nem szerepelt:

Legyen p>2 prímszám, és tekintsük a

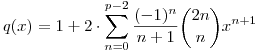
$q(x)=1+2\cdot\sum_{n=0}^{p-2}\frac{(-1)^n}{n+1}\binom{2n}{n}x^{n+1}$

egész együtthatós polinomot. Bizonyítsuk be, hogy q-nak van gyöke modulo p, azaz létezik olyan x egész, hogy q(x) osztható p-vel.

Példa: p=7 esetén a polinom:

q(x)=1+2x-2x²+4x³-10x⁴+28x⁵-84x⁶.

Ennek az értéke pl. x=5 esetén q(5)=-1230789 osztható 7-tel, azaz p=7-re az állítás teljesül.

Továbbá megkönnyítendő az ellenőrzést, elárulom, hogy p=3, 5, 7, 11, 13, 17, 19 esetén az alább x-ek rendre jó választást adnak: x=2, 1, 5, 8, 3, 4, 14.

[700] vogel	2011-12-28 22:36:27
Ha az 1-et tekinti egységnek, akkor 2 inverze 4 mod 7, ha a szorzás a művelet.

[699] Kemény Legény	2011-12-28 22:14:29
Azért az nem kellene elfelejteni, hogy testben lehet osztani 0-tól különböző elemmel, és a 7 szerencsés módon egy prím, ezért a mod 7 maradékosztályok testet alkotnak.
Előzmény: [697] HoA, 2011-12-28 21:31:30

[698] Füge	2011-12-28 21:50:22
Kongruenciát úgy oszthatsz, ha a mod-ot is leosztod a mod és az osztó legnagyobb közös osztójával. Tehát a 2 kongruens 8 (mod 6)-ból következik, hogy 1 kongruens 4 (mod 3).
Előzmény: [697] HoA, 2011-12-28 21:31:30

[697] HoA	2011-12-28 21:31:30
De ezt ugye butaságnak tartjuk? Még egészekre sem igaz ilyesmi. Pl. 2 kongruens 8 ( mod 6 ) -ból nem következik 1 kongruens 4 ( mod 6 )
Előzmény: [695] Hölder, 2011-12-27 00:03:56

[696] Zormac

2011-12-27 01:07:59

Nem túl elegáns, hogy az egyes csak két darab kilencesből áll. Lehetett volna például ez, vagy ezerféle más:

$\frac{9}{\sqrt{9}\sqrt{9}}$

Előzmény: [692] jonas, 2011-12-24 12:25:32

[695] Hölder	2011-12-27 00:03:56
1/2 "kongruens" 4 mod 7 ,hiszen 1 kongruens 8 mod 7. Szerintem erre gondoltak.
Előzmény: [694] lorantfy, 2011-12-26 21:56:47

[694] lorantfy	2011-12-26 21:56:47
Ezt nem is lehet olyan könnyen helyrehozni, mint az előzőt. Nem is tudom mit akartak ezzel a -1-es kitevővel?
Előzmény: [693] Róbert Gida, 2011-12-24 18:12:43

[693] Róbert Gida	2011-12-24 18:12:43
Ez sem jó óra, 2^-1mod 7 egy maradékosztály és nem egyenlő 4-gyel.
Előzmény: [688] lorantfy, 2011-12-23 14:12:49

[692] jonas

2011-12-24 12:25:32

Bizonyára azt akarta 5 órához írni, hogy

$(\sqrt{9})! - \frac{9}{9}$

Előzmény: [691] lorantfy, 2011-12-24 11:50:59

[691] lorantfy	2011-12-24 11:50:59
Mit szúrt el az óra készítője? Hogy lehetne a legegyszerűbben javítani?
Előzmény: [689] jonas, 2011-12-23 22:03:58

[690] Füge	2011-12-23 23:01:15
A k! eleve négyzetszám se lehet :) (kivéve k=0,1)
Előzmény: [689] jonas, 2011-12-23 22:03:58

[689] jonas	2011-12-23 22:03:58
A faktoriálisos kifejezés (5 óránál) az túl nagy szerintem. 9! az legalább százezer, annak a gyöke is legalább száz, ha abból kivonunk 9/9-et, az még mindig legalább száz.
Előzmény: [687] lorantfy, 2011-12-23 13:10:32

[688] lorantfy	2011-12-23 14:12:49
Ha mindet érted, akkor matematikus BSC diploma! :-)

[687] lorantfy	2011-12-23 13:10:32
Hol a hiba? 10 másodperced van, hogy kitaláld! 10, 9, 8...

[686] Lóczi Lajos	2011-11-29 17:24:07
Nem inkább az 1:(1,25^.10²⁰) kifejezést akartad írni?
Előzmény: [685] patba, 2011-11-29 16:36:48

[685] patba	2011-11-29 16:36:48
Értettem a feladatot, de az FBI nem 9 pontos ujjlenyomatot tárol/használ, hanem 12 pontost. Ekkor 1:1,25^.10²⁰ az esélye annak, hogy két különböző ember ujjlenyomata megegyezzen, legalábbis Osterburg szerint. Így viszont már hihető, hogy a 200 millió között nincs két egyforma.
Előzmény: [683] Kemény Legény, 2011-11-29 09:37:24

[684] Róbert Gida	2011-11-29 16:07:55
Helyes. A probléma lényegében a születésnap paradoxon: http://en.wikipedia.org/wiki/Birthday_problem
Előzmény: [683] Kemény Legény, 2011-11-29 09:37:24

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?