|
| [807] w | 2013-04-29 16:36:16 |
 Legyenek a, b és c egész számok. Igazoljuk minél egyszerűbben, hogy a következő kifejezés is egész szám lesz:
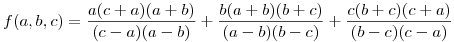
.
|
|
| [806] w | 2013-04-29 16:35:35 |
 Az írás leginkább csak az alapdolgokat tárgyalja. A karakterisztikus egyenlet gyökei stb. konjugált párok, így nem lesz sok baj a komplex képlettel sem, de ahogy Lóczi Lajos is mondta, a valós képlet (mivel ha nem is feltétlenül zárt alakban, de létezik --> binom. tétel) kinyerhető.
|
| Előzmény: [801] logarlécész, 2013-04-28 13:47:47 |
|
|
|
|
|
| [801] logarlécész | 2013-04-28 13:47:47 |
 Köszönöm a linket! Melyik fejezetre gondoltál? Mert én magamtól a másodrendű rekurziók között keresgéltem, de ott csak a "két mértani sor összege" típusú megoldást láttam ide illőnek, ami komplex végeredményt adott (nekem). Ezért is merült föl bennem a kérdés, hogy van-e ill. hogyan határozható meg a valós képlet.
|
| Előzmény: [799] w, 2013-04-28 12:53:20 |
|
|
|
|
| [797] logarlécész | 2013-04-28 12:02:56 |
 Igen, én is látom, hogy kihagytam a rekurzióból, hogy csak n>2 egészekre igaz az állítás... :-)
|
|
| [796] logarlécész | 2013-04-28 11:58:34 |
 Adott a következő sorozat:
a1=1, a2=3, an=2an-1-3an-2
A sorozat szemmel láthatóan csak valós (egész) elemeket fog tartalmazni. A kérdés: található-e a sorozathoz csak valós számokat használó explicit képlet? (Komplex számokat használó explicit képlet nyilván van, két mértani sor összegeként...)
Minden megoldási javaslatot (ill. végeredményt is) köszönettel fogadok!
|
|
| [795] w | 2013-04-10 16:32:56 |
 Ez kicsit trollkodás, szerintem tudod, mire gondolok. Úgy értem, hogy két tétel akkor ekvivalens, ha "közvetlenül" következnek egymásból. A kitűzött feladat nyilván vitatható, ezért is fórumon érdemes megbeszélni.
|
| Előzmény: [794] Sinobi, 2013-04-09 16:38:45 |
|
| [794] Sinobi | 2013-04-09 16:38:45 |
 Az egyikből következik, hogy 1=1, és abból, hogy 1=1 következik a másik...
Teljesen biztos vagy abban, hogy tételek körében értelmes ekvivalenciáról beszélni? Definícióknál szoktak, meg esetleg ha kikötöd, hogy milyen axiómákat szabad használni.
|
| Előzmény: [791] w, 2013-04-09 07:22:46 |
|
| [793] w | 2013-04-09 07:27:26 |
 Az egyenlőtlenségek alkalmas alkalmazására + esetleg némi határértékszámításra gondolok, de az irracionális súlyokat szerintem most zárjuk ki.
|
| Előzmény: [791] w, 2013-04-09 07:22:46 |
|
|
|
| [790] Sinobi | 2013-04-08 23:21:15 |
 Mit jelent az, hogy ekvivalensek egymással? Ha a valós számok axiómáit használhatom, akkor mindegyik állítás igaz, kész. Ha nem használhatom, akkor..?
|
| Előzmény: [789] w, 2013-04-08 21:10:52 |
|
| [789] w | 2013-04-08 21:10:52 |
 Na, ez talán népszerűbb lesz. Tekintsük a következő egyenlőtlenségeket: AM-GM, Hölder, AM-QM, Titu-lemma, Cauchy.
a) Mutassuk meg, hogy utóbbi három ekvivalens egymással.
b) Igazoljuk, hogy utóbbi négy az elsőből következik.
c) Igaz-e, hogy mind az öt ekvivalens egymással?
|
|
| [788] w | 2013-04-07 20:22:22 |
 Nincs sok érdeklődő, úgyhogy elmondom: osszuk el 1012345678-at 1012345678-1-gyel. Ha "kiepszilonozzuk" az ezeknél megszokott módon, láthatóan igaz lesz az állítás (pl. 0,999...=1 esetén). Másképpen: a, 2a, ..., ma teljes maradékrendszer modulo m, ha (a,m)=1.
|
| Előzmény: [787] w, 2013-04-01 23:59:28 |
|
| [787] w | 2013-04-01 23:59:28 |
 Ez kicsit nehéz lesz a témához képest, de idevaló.
Nevezzük periódusnak egy végtelen, szakaszos tizedes törben fellelhető legrövidebb szakaszt. Elérhető-e egy pontosan 12345678 hosszú periódus?
|
|
| [786] Sinobi | 2013-03-30 17:33:13 |
 Ez egyszerű. A Pitagorasz-tétel miatt azok a pontok, melyekből tB hoszú érintő húzható, a k O középpontjától 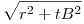 messze lesznek. Azok a pontok, amelyek A-tól tA+tB távolságra vannak, egy A középpontú tA+tB sugarú körön lesznek. A két kör két metszése lehet csak B, azaz csak két ilyen különböző B pont létezik (adott r,O,a,tA,tB esetén), de az olyan két pont, ahol AB érintő triviálisan jó tehát azok azok. messze lesznek. Azok a pontok, amelyek A-tól tA+tB távolságra vannak, egy A középpontú tA+tB sugarú körön lesznek. A két kör két metszése lehet csak B, azaz csak két ilyen különböző B pont létezik (adott r,O,a,tA,tB esetén), de az olyan két pont, ahol AB érintő triviálisan jó tehát azok azok.
|
| Előzmény: [785] HoA, 2013-03-30 13:17:02 |
|
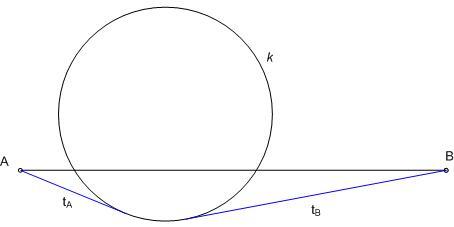
| [785] HoA | 2013-03-30 13:17:02 |
 A k körön kívüli A ill. B pontokból a körhöz húzott érintő szakaszok hossza tA ill. tB . Igazoljuk, hogy ha AB=tA+tB, akkor ( az ábrával ellentétben ) AB érintő.
|
 |
|
| [784] w | 2012-12-24 13:31:34 |
 Elegáns megközelítés. Más megoldás: 10-zel osztunk, majd AM-GM miatt triviális. Ha a változók szorzata 1, vagy összege 1, akkor AM-GM majdnem mindig beválik. Emiatt a feladatot rendezési tétellel is meg lehet oldani, illetve visszavezethető teljes négzetekre (itt talán az is kiszúrná a szemünket).
|
| Előzmény: [783] HoA, 2012-12-24 09:55:21 |
|







