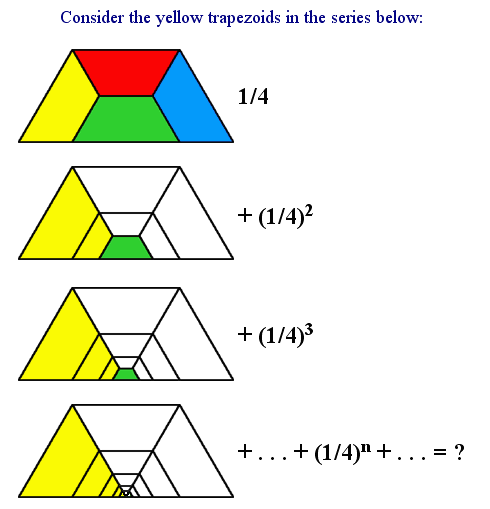| [82] Hajba Károly | 2004-01-16 14:14:19 |
 26. feladat
Vegyünk egy a alapú m magasságú egyenlő szárú háromszöget. Az alap P1 és P2 pontjából a szárak oldalfelező pontjaira (Q1,Q2) merőlegest tudunk állítani. Mennyi P1P2 ill. P1Q1 szakaszok hossza?
HK
|
|
| [81] Gubbubu | 2004-01-15 01:17:11 |
 Üdv;
Még két hasonló feladat: (nem nehezek, legalábbis az első, a másodikhoz kell egy kis térlátás)
24.feladat: Legyenenek az 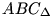 a,b oldalainak felezőpontjai F,G, súlyvonala S. Lássuk be, hogy az a,b oldalainak felezőpontjai F,G, súlyvonala S. Lássuk be, hogy az  és az és az 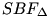 háromszögek végszerűen egyenlőek, azaz átdarabolhatóak egymásba, és adjunk meg egy konkrét átdarabolást is. háromszögek végszerűen egyenlőek, azaz átdarabolhatóak egymásba, és adjunk meg egy konkrét átdarabolást is.
25.feladat: Igazoljuk, hogy egy a,b,c oldalú, m testmagasságú paralelepipedon és egy a,b oldalú paraleogramma alapú, m magasságú téglatest térfogata megegyezik!
Segítség: persze át kellene darabolni a testeket...
|
|
| [80] Gubbubu | 2004-01-14 20:35:24 |
 Kedves R.B.!
Jól emlékszel, a tétel úgy szól, és valóban Bolyai F. tételének hívják. A bizonyítása tényleg nem túl nehéz, bár egy kissé hosszadalmas, szerintem nem illik ebbe a rovatba.
Én azonban, ha elvártam volna valamit, akkor az egy konkrétabb bizonyítás, mondjuk egy ábra lett volna. Persze nem vártam el semmit, még azt sem, hogy akadjon valaki, aki megoldja a feladatot és fölteszi a megoldást, csak azért tűztem ki, hátha valakinek kedve van ilyesmiken is gondolkodni, amikor fáradt egy nehezebb probléma megoldásához.
Üdv: G.
|
|
| [79] Rácz Béla | 2004-01-14 01:45:16 |
 Azt hiszem, tétel szól ennek a feladatnak az általánosabb formájáról, azaz hogy bármely két egyenlő területű sokszög véges sok vágással átdarabolható egymásba. Úgy emlékszem, hogy ezt Bolyai Farkas tételének is hívják. A bizonyításhoz nem kell igazán újító ötlet, úgyhogy akár ezt is meg lehetne itt kérdezni.
|
| Előzmény: [78] Gubbubu, 2004-01-14 00:55:24 |
|
| [78] Gubbubu | 2004-01-14 00:55:24 |
 Egy ujabb egyperces:
Lássuk be, hogy tetszőleges (nem elfajult) háromszög bármely súlyvonala a háromszöget két olyan részháromszögre osztja, amelyek végszerűen egyenlőek (azaz véges sok síkidomra vágással átdarabolhatóak egymásba)!
|
|
| [77] Gubbubu | 2004-01-10 01:44:24 |
 Üdvözlet mindenkinek!
Mára egy kedves, bár nem túlságosan új kis feladatot hoztam - ugye nem baj? - szerintem néhány perc alatt megoldható, így ebbe a rovatba teszem:
kb. 22. feladat:
Oldjuk meg a
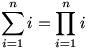
vagy ha úgy jobban tetszik,
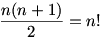
egyenletet (n N)! N)!
(már megint a háromszögszámok!)
|
|
|
| [75] Hajba Károly | 2004-01-08 10:59:49 |
 A pontosított megoldás a 21. feladatra:
Négyzetszám csak (0, 1, 4, 5, 6, 9) számokra végződhet, így ha ebből 5-öt levonunk, a 2n csak (4, 6) számokra végződhet. Ebből következik, hogy felírhatjuk 4n formában is, ami négyzetszám. Tehát 2 db négyzetszám különbsége 65|5*13|1*65.
(x+i)2-x2=65
i*(2x+i)=65
x={9,33}
n=log2(x2-65)={4,10}
Tehát csak ez a két megoldás létezik.
HK
|
| Előzmény: [74] Hajba Károly, 2004-01-08 09:44:35 |
|
| [74] Hajba Károly | 2004-01-08 09:44:35 |
 Megoldás a 21. feladatra:
Négyzetszám csak (0, 1, 4, 5, 6, 9) számokra végződhet, így ha ebből 5-öt levonunk, a 2n csak (4, 6) számokra végződhet. Ebből következik, hogy felírhatjuk 4n formában is, ami négyzetszám. Tehát 2 db négyzetszám különbsége 65|5*13|1*65.
(x+i)2-x2=65
i*(2x-i)=65
x={9,33}
n=log4(x2-65)={4,33}
Tehát csak ez a két megoldás létezik.
HK
|
| Előzmény: [72] Suhanc, 2004-01-07 20:45:54 |
|
|
| [72] Suhanc | 2004-01-07 20:45:54 |
 Hahó!
Mintha most kissé ritkábban kerülne fel feladat...;)
Ez tényleg egyperces:
21. feladat
Mely pozitív egész n értékre lesz
2n+65 négyzetszám?
|
|
|
| [70] gongadze | 2004-01-04 23:43:10 |
 Sziasztok!
Ebbe az egyszerű problémába ütköztem és nem tudok továbblépni:
» Az előző+1. példa:
Van 5 különböző súly és egy kétkarú mérleg... súlyok szerint kéne rendezni.. a kétkaru mérleg csak összehasonlítani tud.. abszolut mértéket nem mutat.. hány mérés kell a legjobb algoritmus esetében?..és persze hogy működik a legjobb algoritmus?
Előre is kösz a visszajelzéseket :]
|
|
| [69] Csizmadia Gábor | 2004-01-02 16:39:56 |
 Ez igaz.:-) Nem fejtettem ki részletesebben, hogy mit értek periodicitás alatt, tkp. rossz kifejezést használtam.
Írjuk fel x=0,... alakban a tizedesvessző mögé sorba a differenciasorozat tagjait. És az a kérdés, hogy ez a szám racionális-e? ((legyen 18b))
|
| Előzmény: [63] lorybetti, 2003-12-29 14:52:31 |
|
|
| [67] lorantfy | 2003-12-31 21:22:54 |
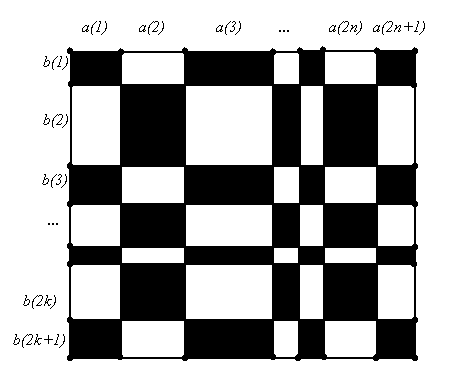
 Megoldás a 20. feladatra:
Osszuk fel az A és B oldalú téglalap oldalait az ábra szerint! A fekete mezők területének összege:
b1a1+b1a3+…+b1a2n+1+b2a2+b2a4+…+b2a2n+…+
+b2ka2+b2ka4+…+b2ka2n+b2k+1a1+b2k+1a3+…+b2k+1a2n+1=
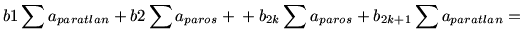
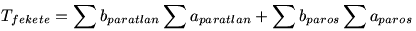
Hasonlóan a világos mezők területének összege:
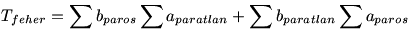
Mivel Tfekete=Tfeher
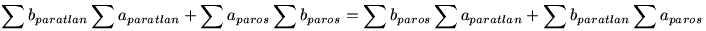
Rendezve:
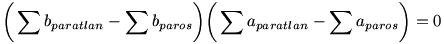
Ez azt jelenti, hogy legalább az egyik különbségnek nullának kell lenni.
Tehát pl. 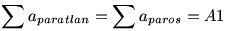 . Ez pedig pont azt jelenti, hogy a sötét mezőket balra tömörítve összetolva egy A1 oldalú téglalap jön létre, melynek másik oldala az eredeti téglalap B oldala. . Ez pedig pont azt jelenti, hogy a sötét mezőket balra tömörítve összetolva egy A1 oldalú téglalap jön létre, melynek másik oldala az eredeti téglalap B oldala.
|
 |
| Előzmény: [66] Suhanc, 2003-12-29 17:34:09 |
|
| [66] Suhanc | 2003-12-29 17:34:09 |
 20. feladat
Egy téglalapot oldalaival párhuzamos egyenesekkel felosztunk n sorra és n oszlopra. Ezután a cellákat sakktáblaszerűen kiszínezzük. A fekete mezők területének összege megegyezik a fehér mezők területének összegével. Bizonyítandó, hogy a fekete mezőkből téglalap alkotható!
|
|
| [65] Suhanc | 2003-12-29 17:24:48 |
 Megoldás a 19. feladatra:
Meghatározandó az 1/4+1/42+1/43+... összeg. Legyen
(1)1/4+1/42+1/43+... =a
Ekkor: (2) 1+1/4+1/42+1/43+...=4a
(2)-(1): 1=3a Tehát a=1/3
Nem vagyok biztos benne, de azt hiszem itt még be kell látni, hogy ez az összeg valóban létezik... ha ezt beláttuk,készen vagyunk; talán nélküle is ;)
|
|
| [64] lorantfy | 2003-12-29 14:59:05 |
 19. feladat: Bizonyítsd be az ábra szerinti állítást! (A szemléletes ábrasort a math.rice.edu lapról ollóztam.)
|
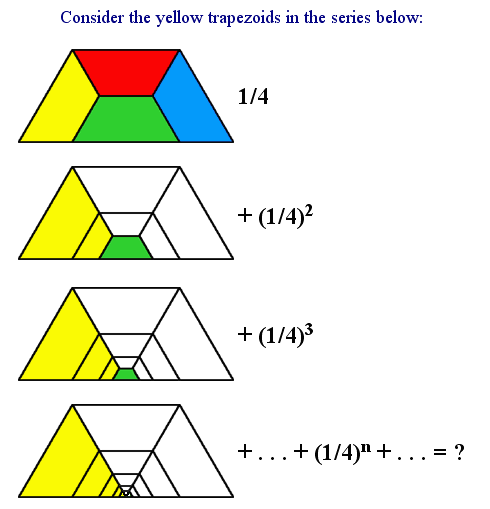 |
|
|
|
|
| [60] Csizmadia Gábor | 2003-12-27 18:12:05 |
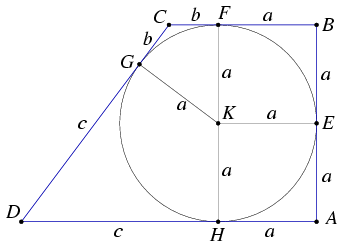
 Az állítás igaz. Sajnos ábrát nem tudok mellékelni. (még nem tanultam meg kezelni az ábraszerkesztőt)
Ha a trapéznek van egy derékszögű csúcsa, mivel az egyik szögszárral a definíció miatt van egy párhuzamos oldala, ezért van még egy derékszögű csúcsa is. Legyen a két derékszögű csúcs A és B, a másik kettő C és D, és ezek a pontok a trapéz pontjai ilyen sorrendben. Belerajzoljuk a kört, ennek sugara legyen r, középpontja K. Az érintőszakaszok egyenlőek, ezért az oldalakat az alábbi módon lehet felírni másként: AB=a+d; BC=d+b; CD=b+c; DA=c+a Az ábráról azonnal látszik (a két derékszög miatt), hogy a=d, ezért AB=2a; BC=a+b. Írjuk fel a két párhuzamos oldalt szorzatát, és a területet is a,b és c-vel kifejezve. T=(BC+AD)*m/2 A két derékszög miatt a magasság (m)=2a. így T=(2a+b+c)*a=2aa+ab+ac AD*CB pedig = (a+b)(a+c)=aa+ac+ab+bc Be kell bizonyítani, hogy ez a két kifejezés megegyezik, tehát különbségük 0. A kettőt egymásból kivonva (aa-bc)-t kapunk, ha ez 0, akkor aa=bc. Ennek bizonyításához belátjuk, hogy AKB=CKD=90fok. A kör érintse AB-t E-ben, BC-t F-ben, CD-t G-ben, DA-t H-ban. Az ábra elrendezéséből azonnal adódik, hogy BF, EK és AH párhuzamos, valamint AB és FH is párhuzamos. Emiatt a=BF=EK=r, tehát K AB Thalész-körén van, vagyis AKB derékszög. A szimmetria miatt GH és KD; illetve KC és FG egymásra merőlegesek, az előbbi kettő metszéspontja legyen M, az utóbbi kettőé N. Mivel FH átmérő, ezért FGH szög derékszög. Beláttuk tehát, hogy KMGN négyszög három szöge derékszög, következésképp a negyedik szöge is az, amit éppen kerestünk (CKD). AKB illetve CKD derékszögű háromszögek, ezért érvényes bennük a magasságtétel. Tehát aa=rr, illetve bc=rr. Emiatt aa=bc, amit bizonyítani akartunk. (Bocsi a hosszú leírásért.)
|
| Előzmény: [59] kdavid, 2003-12-27 13:07:08 |
|
| [59] kdavid | 2003-12-27 13:07:08 |
 Sziasztok!
A feladat, amivel nem sikerült megbírkóznom a következQ: Egy trapéz egyik szöge 90 fok és a trapézba kör irható. Igazold, hogy a trapéz területe a két párhuzamos oldal szorzata.(Lehet, hogy az egyik állítás is elég a bizonyításhoz.) Ha az állítás nem igaz az is segít!
Ha tudtok segíteni azt megköszönöm.
|
|
| [58] lorantfy | 2003-12-24 21:04:27 |
 Kiegészítés a 17. feladat megoldásához:
Kaptam egy visszajelzést, hogy nem zártam ki azt az esetet, hogy a szorzat két tagja esetleg egy prímszám különböző hatványa. Most pótolom:
Ha a szorzat egyik tagja pk másik pm lenne, akkor a különbségükből p kiemelhető lenne. De a két páratlan szám különbsége páros (4n), így csak p=2 lehetne, de a páratlan számoknak ez nem lehet osztója.
|
| Előzmény: [55] lorantfy, 2003-12-24 00:16:18 |
|





 N)!
N)!