|
|
| [826] nadorp | 2013-05-02 13:44:57 |
 Remélem, ez már jó megoldás lesz.
Tekintsük a következő p(x)polinomot. ( a b b c) c)
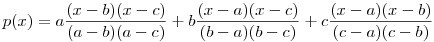
Látszik, hogy a p(x)=x egyenletnek az a,b és c különböző gyökei. Mivel egy másodfokú egyenletnek csak két különböző gyöke lehet, ez csak úgy lehet, ha a p(x)=x egyenlet azonosság, tehát minden x-re

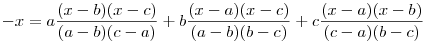
Behelyettesítve az x=a+b+c értéket
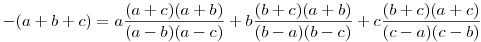
|
| Előzmény: [825] nadorp, 2013-05-02 13:29:00 |
|
|
| [824] nadorp | 2013-05-02 13:24:21 |
 Tekintsük a p(x)=x polinomot. Ekkor p(a)=a, p(b)=b és p(c)=c. Írjuk fel a Lagrange interpolációs képletet. Kapjuk, hogy minden x-re

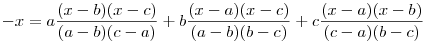
Behelyettesítve az x=a+b+c értéket

|
| Előzmény: [807] w, 2013-04-29 16:36:16 |
|
|
|
| [821] jonas | 2013-04-30 23:31:34 |
 Ja értem! Azt mondod, hogy a közös nevezőre hozás után g alternáló, vagyis g(a,c,b)=-g(a,b,c), ezért (b-c) osztóha g-nek. Hasonlóan (a-b) és (c-a) is osztója. Így aztán h osztója g-nek.
Most g/h a fokszámok miatt elsőfokú polinom. Mivel viszont g(b,c,a)=g(a,b,c) és h(b,c,a)=h(a,b,c), ezért az elsőfokú hányados csak a+b+c skalárszorosa lehet.
Ügyes megoldás.
|
| Előzmény: [820] Fálesz Mihály, 2013-04-30 23:02:25 |
|
| [820] Fálesz Mihály | 2013-04-30 23:02:25 |
 A függvény egy háromváltozós racionális tört. A nevezője a Vandermonde-polinom.
A függvény szimmetrikus. Mivel a nevező alternáló, a számláló is alternáló.
Ha viszont a számláló alternáló, akkor osztható a Vandermonde polinommal.
Tehát a számláló osztható a nevezővel, a tört valójában egy polinom.
|
| Előzmény: [819] jonas, 2013-04-30 21:00:53 |
|
|
| [818] w | 2013-04-30 19:38:17 |
 "Ha csak ki akarjuk számolni. akkor érdemes előbb két tagot összeadni, egyszerűsíteni, és csak utána hozzáadni a harmadik törtet."
Nem mondod! Másik lehetőségünk (a korábbi két megoldás): közös nevezőre hozás után megnézzük a tagokat külön-külön. Lehet 'ügyesen számolni'.
Említetted, hogy "a kifejezés polinom, mert a közös nevező alternáló". Ezt részletesebben is kifejtenéd, mert a feladat annyit kér, hogy f(a,b,c) egész?
|
| Előzmény: [817] Fálesz Mihály, 2013-04-30 18:59:33 |
|
| [817] Fálesz Mihály | 2013-04-30 18:59:33 |
 Ha csak ki akarjuk számolni. akkor érdemes előbb két tagot összeadni, egyszerűsíteni, és csak utána hozzáadni a harmadik törtet.
* * *
Ha dózerolni akarunk, akkor megállapítjuk, hogy
--- a kifejezés szimmetrikus
--- a kifejezés polinom, mert a közös nevező alternáló
--- a polinom homogén elsőfokú.
Tehát f(a,b,c)=K.(a+b+c) valamilyen K konstanssal.
A konstanst valamilyen konkrét számhármas (pl. -1,1,2) behelyettesítésével is megkaphatnánk, de ez ellentétes lenne a dózerolás filozófiájával. ;-) Ezért inkább a fájdalom- és számolásmentes 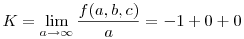 határértéket vesszük (rögzítve b-t és c-t). határértéket vesszük (rögzítve b-t és c-t).
|
| Előzmény: [816] w, 2013-04-30 16:44:54 |
|
| [816] w | 2013-04-30 16:44:54 |
 Ez tetszik. Én egyszerűen felszoroztam. Kaptam a két oldalon egy-egy háromtagú ciklikus összeget:
a(...)+b(...)+c(...)=a(...')+b(...')+c(...')
Ezeknek első tagjait vetettem össze egymással. A dolgok szépen kiesnek, elkerülhetjük a sok számolást.
|
| Előzmény: [815] jonas, 2013-04-30 15:00:35 |
|
| [815] jonas | 2013-04-30 15:00:35 |
 Mutatok egy megoldást, bár gyanítom, hogy van ennél egyszerűbb is.
Hozzuk a kifejezést közös nevezőre. f=g/h, ahol
g=a(c+a)(a+b)(b-c)+b(a+b)(b+c)(c-a)+c(b+c)(c+a)(a-b),
h=(a-b)(b-c)(c-a).
Fejtsük ki először a nevezőt, mert az könnyebb.
h=-a2b+b2a-b2c+c2b-c2a+a2c.
Most nézzük a számlálót! Fejtsük ki a három tagot külön.
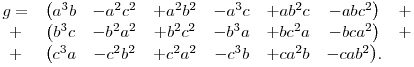
Ebben vannak azonos tagok, amik kiejtenék egymást, de a trükk az, hogy nem ejtjük ki őket. Helyette forgassuk el az egyes oszlopokat külön-külön: a második és negyedik oszlopot forgassuk fölfelé, a hatodikat lefelé.
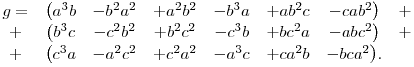
Most a sorokat szorzattá alakíthatjuk:
g=ab(a+b+c)(a-b)+bc(a+b+c)(b-c)+ca(a+b+c)(c-a)=
=(a+b+c)(a2b-b2a+b2c-c2b+c2a-a2c)=-(a+b+c)h.
Ebből pedig f=-(a+b+c) egész szám, feltéve, hogy h nem nulla. Ha h nulla, akkor valamelyik tényezője nulla, ettől pedig f eredeti alakjában valamelyik nevező nulla lesz.
|
| Előzmény: [807] w, 2013-04-29 16:36:16 |
|
|
|
| [812] w | 2013-04-29 22:28:07 |
 A feladatoddal még nem volt időm foglalkozni, ha arra céloztál, de majd gondolkozom rajta. Másrészt akkor megkérdezném, hogy melyik ördöngös módszerrel igazoltad az f(a,b,c)=-(a+b+c) azonosságot?
|
| Előzmény: [811] Lóczi Lajos, 2013-04-29 22:15:13 |
|
| [811] Lóczi Lajos | 2013-04-29 22:15:13 |
 "olyan egyszerű alakja van"
Egyszerű? Micsoda egybeesés, szerintem a g polinom együtthatói az "Érdekes matekfeladatok" [3717]-es hozzászólásában szereplő összegekkel fejezhetők ki!
|
| Előzmény: [810] w, 2013-04-29 21:31:33 |
|
| [810] w | 2013-04-29 21:31:33 |
 Tudom, ez szubjektív kérdés. Én ciklikus permutációkkal láttam be, úgy nem bonyolódunk bele a dologba. A kérdés, hogy lehet-e ezt nem dózerolni?
A többieknek: a Lajos által definiált g polinom rövid kísérletezéssel megkapható, még interpolálni se kell, olyan egyszerű alakja van :)
|
| Előzmény: [809] w, 2013-04-29 21:27:10 |
|
|
|
| [807] w | 2013-04-29 16:36:16 |
 Legyenek a, b és c egész számok. Igazoljuk minél egyszerűbben, hogy a következő kifejezés is egész szám lesz:
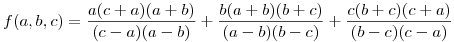
.
|
|
| [806] w | 2013-04-29 16:35:35 |
 Az írás leginkább csak az alapdolgokat tárgyalja. A karakterisztikus egyenlet gyökei stb. konjugált párok, így nem lesz sok baj a komplex képlettel sem, de ahogy Lóczi Lajos is mondta, a valós képlet (mivel ha nem is feltétlenül zárt alakban, de létezik --> binom. tétel) kinyerhető.
|
| Előzmény: [801] logarlécész, 2013-04-28 13:47:47 |
|
|
|





 b
b
