Fórum: "ujjgyakorlatok"

Javítottam kicsit, ezt nézd meg, kérlek!

Egy részét nem tudta értelmezni, volt nálam is ez az érték, pillanat, és utána nézek.

Érdekes, nálam a szorzat értéke közelítőleg:

4,2476010824943749265068611568271227122719037x\(\displaystyle 10^{13}\). Hol a bökkenő? :)

Nagyon idevág egy újraértelmezett felírási mód a nevezetes szögekre vonatkozóan, akit érdekel, azzal ezt is megosztom, lényegében ezek is segíthetik a témában a kutatómunkát:

sin(20deg) és sin10(deg) megadása

Pontos szögfelírás új metodikája 1.

Pontos szögfelírás új metodikája 2.

A megadott értéknél véletlenül hányadost írtam, de itt a megígért szorzat is:

Szorzat

A konkrét választ sajnos nem találtam meg, de egy apró részeredmény alapján a kitartóbbak elindulhatnak megkeresni, de nem biztos, hogy várható szép eredmény. Ahol valós értékek vannak, ott a Wolfram kiszámolta a közelítést, amit irracionális szorzatként is fel tudtam írni némi kutató munka árán és természetesen a Wolfram segítségével. Íme.:

Közelítés

Pontosabb érték

Chloe-ról eddig nem volt szó, ő is pizzázni ment?

Azért írtam oda, hogy számít az egy oszlopon lévő korongok sorrendje, mert ha az első oszlopon egy piros korong van alul és azon két kék korong, az eltérő elrendezés, mint ha a piros korong lenne középen, fölötte és alatta egy-egy kék korong.

A pizzériás feladatnak van előzménye is, amiben még Chloe össze volt veszve mindenkivel?

Onnan vagyok benne biztos, hogy n=6-ra ezzel pont kijön a 40193. A te feladatod meg elég hiányos, számít-e, hogy az egyes embernek ki a "bal" oldali szomszédja, vagy csak az, hogy mely 2 ember a szomszédja. Az meg, hogy Bea és Cili közben kibékültek gondolom csak felesleges adat. Nyilván ez semmiképpen sem lehetne ebben a formában mondjuk egy érettségi feladat.

Akkor vajon miért van ott a mondat? Honnan tudod, hogy a kitűző mire gondolt? Ezt hogy oldanád meg?

A mozi után Anna, Bea, Cili és Dóra beültek egy pizzériába egy kerek asztal köré. Hányféleképpen ülhettek le, ha közben Bea és Cili kibékültek?

11-es tankönyv.

"Az egy oszlopon lévő korongok sorrendje is számít, mert nem tudnak helyet cserélni egymással." ezt a mondatot akár ki is lehetett volna hagyni. A korongok nincsenek számozva, mindegy milyen sorrendben tesszük az oszlopra a korongokat. Csak az számít, hogy a (számozott!) rudakon hány korong van és azokon az egyes korongok piros vagy kék oldala van-e felül.

Nem értem, mit jelent az, hogy a korongok sorrendje számít. Ha azt, hogy meg vannak számozva eleve, akkor persze más a válasz. Ha azt, hogy megszámozzuk őket, miután kiderült melyik oszlopon vannak, akkor is. Az idézett képletben \(\displaystyle \binom{n+k-1}{k}\cdot 2^k\)-van, ez azt jelenti, hogy mindegy milyen sorrendben tesszük az oszlopra a korongokat, csak az számít melyik oldaluk van felül. Ekkor tényleg 40193 leosztás van. A sorrend itt csak abban számít, hogy hanyadiknak van felül a kék illetve piros fele.

n korongra és n rúdra: a(n), és itt a harmadik formulából látható igazán, hogy erről a sorozatról van szó.

A következő összeszámlálási problémát kisiskolás koromban hallottam, amikor még nem tudtam megoldani.

Van egy állványunk hat számozott oszloppal. Van hat egyforma lyukas korongunk, amiknek az egyik oldala pirosra, a másik kékre van színezve. A korongokat az állvány oszlopaira szeretnénk fölrakni, de nem kell minden korongot fölhasználni, egy részét ki is lehet dobni. Két elrendezést különbözőnek tekintünk a szerint, hogy melyik oszlopon hány korong van, és az egyes korongoknak melyik színű oldala van felül. Az egy oszlopon lévő korongok sorrendje is számít, mert nem tudnak helyet cserélni egymással. A kidobott korongokról nem számít, hogy melyik oldala van felül. Lássuk be, hogy 40193 különböző elrendezés van.

Elvileg kimérhető, de a gyakorlatban nehéz lenne. Az a baj, hogy már az exponenciális lecsengést is nehéz pontosan kimérni, mert valamilyen izotóp mennyiségét kell szétválasztanod az összes többitől. A valóságban radioaktív bomlásnál mindig jelen vannak más atomok is, ami a mérést lehetetlenné teszi.

Vajon egy radioaktív bomlást megfigyelve kimérhető-e az Euler-féle szám, vagy csak az mérhető ki, hogy valami exponenciális a lecsengése, és az alap meg a konstans egymás függvényei?

Legyenek &tex;\displaystyle {a_0} = 0,{a_1} = 2, {a_{n+1}}=\sqrt{2 - \frac {a_{n-1}}{a_n}},&xet; ahol &tex;\displaystyle n\ge1.&xet; Számítsuk ki: &tex;\displaystyle \lim_{n\to\infty}{2^n{a_n}}.&xet;

Egy l betű lemaradt a végéről. A helyes cím: http://www.komal.hu/hirek/anket/2005/anket2005.h.shtml

Sajnos a link nem működik úgy ahogy elképzeltem, megpróbálom újra, ezen az oldalon Gál Péter előadásában olvashatók a bizonyítások: http://www.komal.hu/hirek/anket/2005/anket2005.h.shtm

Köszönet a segítségért, mindenképp szánok rá időt, hogy beleolvassak. Közben azt is megemlítem, hogy saját kérdésemre reflektálva éppen itt a KÖMAL-os hozzászólások között találtam a témába vágó egy-két tételt, amely szintén hasznos lehet valamely későbbi bizonyítás során: Gál Péter előadása

Egy gyors keresés alapján azt hiszem, a következő oldal végigböngészése érdekes lehet: Tilings by Isosceles Right Triangles. Itt alapvetően rengeteg hasonló kérdést mutatnak, de konkrét leszámolást nem láttam, ill. úgy látom, leginkább négyzetet darabolnak fel egyenlő szárú derékszögű háromszögekre: egy nem-triviális szép példa.

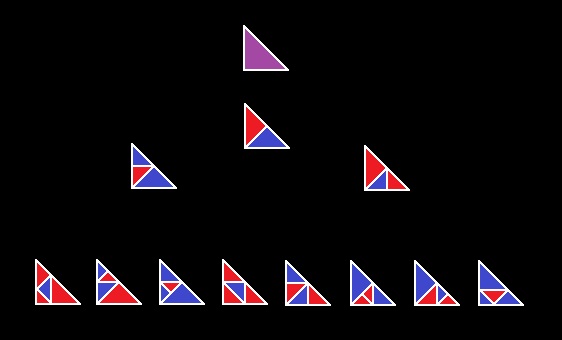
Megértem és köszönöm a javítást. Valóban a szóismétlést szerettem volna elkerülni. (Hányféleképpen lehet megadott számú egyenlőszárú derékszögű háromszöget egymáshoz illeszteni úgy, hogy pontosan egy darab egyenlőszárú derékszögű háromszöget kapjunk? Szándékosan nem jelöltem ki az oldalak mérőszámát, vagyis hogy melyik legyen racionális vagy irracionális, ezt nem tartottam fontosnak a feladat szempontjából. Most inkább egy ábrát mellékelek mivel érdekesnek találtam az ábrán látható alakzatokat, de a színezésnek sincs semmiféle jelentősége. Ezeken látható: f(1)=1 ... f(2)=1 ... f(3)=2 ... f(4)=8 ....és f(5) szerintem legalább 48, de e fölé már nem számoltam, és az általános képletet sem találtam meg. Előfordulhat hogy hibáztam, aki talál új elrendezést, vagy bizonyítást, ami ehhez a témához kapcsolódik, szívesen végig olvasom, de érdekel a kérdésre adott válasz is. A hibákért elnézést kérek. A feladat eredetéről annyit, hogy én nem vagyok matematikához komolyan értő ember, mindössze színes üveg dekoráció készítése közben igyekeztem változatos matematikai jellegű mintázatokat létrehozni, közben vetődött fel a kérdés, hogy a minták készítésében "meddig" mehetek el?

A "szóban forgó síkidom" az "egyenlő szárú derékszögű háromszög" szóismétlésének elkerülése akar lenni? Blikk magazinban elmegy, matek fórumon nem célszerű.

Ha egybevágó háromszögekről van szó, még talán értelmezhető a feladat. De a szöveg arra utal, hogy hasonló háromszögek is megengedhetők.

A javított f(2)=1 szerint hogyan lehet 2 db, pl egy 1 - 1 - &tex;\displaystyle \sqrt 2 &xet; és egy 5 - 5 - &tex;\displaystyle 5 \sqrt 2 &xet; oldalakkal rendelkező háromszöget úgy elrendezni, hogy "pontosan egy darab jöjjön létre a szóban forgó síkidomból" ?

Bocsánat, máris elírtam :) f(2)=1 és f(4)=2, de ettől még áll a kérdés. :)

Sziasztok, én még új vagyok és nem tudom, jó helyre írom-e a kérdésem, de remélem, hogy igen. Egy tangramos (Wikipedia/tangram) feladatra szeretnék rákérdezni, biztos elhangzott már itt (vagy valahol), de sajnos nem találtam meg az útmutatást.

A kérdés:

Hányféleképpen lehet megadott számú egyenlő szárú derékszögű háromszöget úgy elrendezni, hogy pontosan egy darab jöjjön létre a szóban forgó síkidomból?

(A feladatban nincs kikötés a hasonló háromszögek különböző vagy azonos mivoltára, tehát ennek tekintetében kellene számba venni a lehetőségeket is - gondolom, hogy adott k mellett mennyi lehet f(k) értéke ha látható, hogy f(1)=1, f(2)=2, f(3)=2, ... )