Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[203] lorantfy

2004-11-10 10:01:43

Kedves Károly!

Kösz a megoldást! Valóban ennyi az egész.

Előzmény: [201] Hajba Károly, 2004-11-10 07:59:11

[202] Hajba Károly

2004-11-10 08:10:13

59. feladat:

Oldjuk meg az alábbi egyenletet, ha p és q prímek:

p+p²+p⁴-q-q²-q⁴=83.805

[201] Hajba Károly

2004-11-10 07:59:11

57. feladathoz:

m_AB+m_CD=m_Bc+m_DA=1

Azaz egy-egy pont a háromszögeket két egyenlő összterületű részre bontja, s mivel kilenc egyforma területet nem lehet két egyenlő részre bontani, így ilyen elrendezést sem fogunk tudni találni.

Előzmény: [195] lorantfy, 2004-11-09 08:45:18

[200] Hajba Károly

2004-11-09 09:48:05

Kedves KL!

Valóban. Az otthoni vázlatomból rossz sort másoltam ide. Köszi a Kemény-féle kritikát. :o)

Előzmény: [199] Kemény Legény, 2004-11-09 09:38:18

[199] Kemény Legény	2004-11-09 09:38:18
Kedves Onogur!Szerintem az A számod nem (x-3)(x-4) hanem (x-2)(x-5)=x*x-7x+10,ekkor a további folytatás jó.(Bár a megoldásokat nem ellenöriztem le..)
Előzmény: [197] Hajba Károly, 2004-11-09 08:59:01

[198] lorantfy

2004-11-09 09:30:55

Kedves Károly!

Köszönöm! Hát erről van szó. Ha megfelelően párosítjuk a szorzótényezőket az x-ek száma megegyezik, csak konstansban különböznek. Így biztos 3-ad fokú lesz belőle, ami megfelelő n-ekre szépen szorzattá alakítható.

Előzmény: [197] Hajba Károly, 2004-11-09 08:59:01

[197] Hajba Károly

2004-11-09 08:59:01

Egy kis zárójel lemaradt.

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0

A=(x-3)(x-4)=x²-7x+10

(A-4)A(A+2)+16=0

A³-2A²-8A+16=0

$(A-2\bf)\rm(A-2\sqrt{2})(A+2\sqrt{2})=0$

x₁=1,246463...;x₂=1,438447...;x₃=5,753536...;x₄=5,561552...

Előzmény: [196] Hajba Károly, 2004-11-09 08:56:26

[196] Hajba Károly

2004-11-09 08:56:26

Kedves László!

Én is megoldottam, csak Lajos beelőzött. :o)

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0

A=(x-3)(x-4)=x²-7x+10

(A-4)A(A+2)+16=0

A³-2A²-8A+16=0

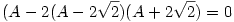
$(A-2(A-2\sqrt{2})(A+2\sqrt{2})=0$

x₁=1,246463...;x₂=1,438447...;x₃=5,753536...;x₄=5,561552...

Előzmény: [195] lorantfy, 2004-11-09 08:45:18

[195] lorantfy	2004-11-09 08:45:18
Kedves Lajos! Gratula! Szép a szorzattáalakítás, de a trükköt is megoszthatnád velünk! Felteszek még egy ábrát az 57. feladathoz hátha valakinek megtetszik!

Előzmény: [194] Lóczi Lajos, 2004-11-09 02:56:16

[194] Lóczi Lajos

2004-11-09 02:56:16

Ha "csak úgy bele a közepibe", akkor

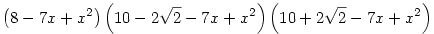$\left( 8 - 7x + x^2 \right) \left( 10 - 2 {\sqrt{2}} - 7x + x^2 \right) \left( 10 + 2 {\sqrt{2}} - 7x + x^2 \right)$ .

Gyártottam még néhány feladatot erre a kaptafára, ezek kivétel nélkül másodfokúak szorzatára bonthatók:

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+n=0, ahol n $\in$ {...,-189,-96,-35,-5,9,15,16,21,64,135,...}.

Persze a tényezők számának és az 1,2,3,4,5,6 számoknak semmi szerepük sincs, pl. (x+1)(x-2)(x+5)(x+4)(x+2)+160=0 egy másodfokú és egy harmadfokú szorzatára bomlik... stb. stb. stb.

Előzmény: [193] Gubbubu, 2004-11-08 19:37:04

[193] Gubbubu

2004-11-08 19:37:04

58. feladat (ezt én Mosóczi András egyetemi hallgatótól ismerem)

Oldjuk meg az alábbi egyenletet:

(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)+16=0

Nem kell megijedni ettől a jó kis hatodfokú egyenlettől. Ügyesen kell szorozgatni és alakítgatni, nem csak úgy bele a közepibe... :-))

[192] lorantfy

2004-11-07 20:00:53

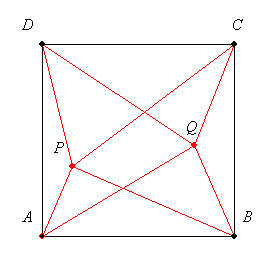
57.feladat: Egy négyzet belsejében úgy vettünk fel két pontot, hogy az ezeket a négyzet négy csúcsával összekötő szakaszok a négyzetet kilenc, közös belső pont nélküli sokszögre darabolják.

Lehet-e a kilenc sokszög területe ugyanakkora?

(Varga Tamás verseny 1998.)

[191] Gubbubu

2004-10-08 09:48:03

56. feladat: Igazoljuk, hogy tetszőleges háromszögben a szokásos jelölésekkel

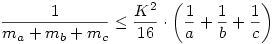
$\frac{1}{ m_{a}+m_{b}+m_{c} } \le \frac{K^{2}}{16} \cdot \left( \frac{1}{a}+ \frac{1}{b} +\frac{1}{c} \right)$

Hálás lennék, ha valaki felvilágosítana, mennyire "jó" ez a becslés, van-e jobb esetleg.

[190] Suhanc	2004-09-22 20:12:54
Ja, ez lemaradt: a;b;c $\ge$ 0

[189] Suhanc

2004-09-22 20:12:09

Elmúlt szakkörön vettük, és egy általános tétel jött ki belőle:

55.Feladat:

Igazoljuk az alábbi egyenlőtlenséget:

a³b+b³c+c³a $\ge$ a²bc+ab²c+abc²

[188] Suhanc	2004-09-22 20:04:08
Mivel senki sem írt, beírom... Az első törtet ${\sqrt 2}$ -vel bővítve a másodikat kapjuk...
Előzmény: [187] Hajba Károly, 2004-09-14 15:02:23

[187] Hajba Károly	2004-09-14 15:02:23
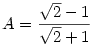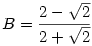54. feladat: Melyik a nagyobb szám, az $A=\frac{\sqrt{2}-1}{\sqrt{2}+1}$ vagy a $B=\frac{2-\sqrt{2}}{2+\sqrt{2}}$ ? HK

[186] V. Dávid

2004-09-04 09:34:31

Az 53-as megoldása:

$x^6-7x^2+\sqrt6=(x^2-\sqrt6)(x^4+\sqrt6x^2-1)=0$

Előzmény: [185] lorantfy, 2004-09-04 09:22:33

[185] lorantfy

2004-09-04 09:22:33

53. feladat: Oldjuk meg a valós számok halmazán az egyenletet:

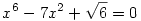
$x^6-7x^2+\sqrt6 = 0$

('96-os OKTV feladat. Mondjuk alakítsuk szorzattá!)

[184] lorantfy

2004-08-17 18:24:31

52. feladat megoldása: x⁴-15x²-18x kifejezés minimumát kell meghatározni elemi módszerekkel.

Jó lenne átalakítani két teljes négyzet összegére, mégpedig úgy, hogy mindkettő ugyanazon x értéknél adjon nullát. A konstans nem számít, majd a végén levonjuk!

x⁴-15x²-18x=(x²-a²)²+b(x-a)²+c

Elvégezve a műveleteket és az azonos kitevőjű tagok együtthatóit összehasonlítva a köv. egyenletrendszert kapjuk:

2a²-b=15

ab=9

c=-a⁴-ba²

Az első kettőből 2a³-15a-9=0, látszik, hogy a=3 gyöke, így szorzattá alakítjuk:

(a-3)(2a²+6a+3)=0, a másodfokú gyökei 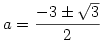$a=\frac{-3 \pm \sqrt3}{2}$ ez mindkettő negatív, 3-nál kisebb absz. értékű és b értéke is negatív.

Emiatt a c=-a⁴-ba² értéke a=3-nál a legkisebb: b=3 és c=-108.

Tehát a konkrét átalakítás:

x⁴-15x²-18x=(x²-9)²+3(x-3)²-108

A kifejezés minimuma x=3-nál -108.

Előzmény: [181] Suhanc, 2004-08-15 12:51:21

[183] ScarMan

2004-08-16 20:14:31

Kedves László!

Mostmár látom, hogy félreértettem a feladatot. Azt hittem, hogy csak azokat a római számokat kell egybeolvasni, amik egymás mellett vannak... hát igen, így már teljesen más a feladat. Bocs az értetlenkedésemért!

Előzmény: [173] lorantfy, 2004-08-15 00:37:02

[182] Hajba Károly

2004-08-15 14:09:48

Kedves Suhanc!

Gratula, egyébként szerintem nincs más megoldás. Ezzel a feladattal még nem mentem a Szabadalmi Hivatalba, így teljes nyugalommal feladhatod. :o)

Hasonló feladatot - arab számokkal - felraktam az "Érdekes matekfeladatok" topikba is [325](74.), ott csak az egyik megoldást találta meg SchZol. Azzal a feladattal már nagyon régen találkoztam először, a római számos változatát most kreáltam, persze ez nem jeleti azt, hogy feltaláltam a spanyolviaszt.

Előzmény: [180] Suhanc, 2004-08-15 12:40:34

[181] Suhanc

2004-08-15 12:51:21

Kedves Mindenki!

Ezzel a feladattal tegnapelőtt találkoztam... egy régi Arany Dani példa... lehet, hogy elsőre kissé favágónak tűnik:

52.FeladatHatározzuk meg az x⁴-15x²-18x kifejezés legkisebb értékét, ha x valós szám!

[180] Suhanc

2004-08-15 12:40:34

Kedves Károly!

Ötletes feladat!:)

Egy lehetséges megoldás: IX;I;II;I;I;I;I

Ha megengeded, majd szeptemberben elkérem...:) Matekórán szoktunk feldobni ilyeneket...

Előzmény: [179] Hajba Károly, 2004-08-15 12:00:03

[179] Hajba Károly

2004-08-15 12:00:03

Ebben a táblázatban

... db I számjegy

... db V számjegy

... db X számjegy

... db L számjegy

... db C számjegy

... db D számjegy

... db M számjegy

található

Hamár a római számoknál tartunk íme az 51. feladat. Természetesen római számjegyekkel kell kitölteni. :o)

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?