| [254] Zoli a vegyész | 2006-02-16 22:03:07 |
 Sziasztok!
Van egy érdekes játékelméleti problémám, vagy ha úgy tetszik programozási feladat:
Két ember Játszik. A kezdő játékos azt mondja, hogy kettő, ezután, pedig mondhat (a kezdő) 2-t 0-t vagy 4-t, ez rá van bízva. Ezután a két játékos felváltva mondogat számokat, de csak olyat mondhat, ami a már elhangzottak összege vagy különbsége (két azonost is össze lehet adni, illetve kivonni), de már elhangzott számot nem lehet mondani. Az nyer, aki először kimondja az 1756-t. Dolgozzunk ki nyerő stratégiát.
Várom válaszaitokat, ha lesz hozzászólás konzultálhatunk fórumon keresztül. Szerintem ez egy érdekes probléma.
Üdv: Zoli
|
 |
|
|
| [252] Lóczi Lajos | 2006-02-15 23:41:28 |
 Sajnos ez nem jó példa: a konvergencia nem egyenletes. (Milyen tétel alapján állítod ezt?)
Periodikus négyszögjel alatt ilyenre gondolsz, igaz? fn pedig a Fourier-sor n-edik részletösszege, ha jól értem; ekkor viszont
a Gibbs-jelenség fellép, ami pont azt jelenti, hogy a Fourier-sor konvergenciája nem egyenletes.
|
| Előzmény: [251] Mate, 2006-02-15 19:19:01 |
|
| [251] Mate | 2006-02-15 19:19:01 |
 Az első feladatra példa: Vegyünk egy olyan f periodikus függvényt, amely nem mindenhol differenciálható, például egy periodikus négyszögjelet. Legyen az fn függvénysorozat e függvény Fourier-sora azzal a módosítással, hogy az n-nél nagyobb indexű együtthatókat zérusnak vesszük. Ez nyilván egyenletesen konvergál a (példánkban) négyszögjelünkhöz, hiszen a Fourier-sor miatt limsup|f-fn|=0.
|
| Előzmény: [249] Lóczi Lajos, 2006-02-14 21:40:03 |
|
|
| [249] Lóczi Lajos | 2006-02-14 21:40:03 |
 Keressünk példát olyan szituációra, hogy
1. minden fn deriválható az egész számegyenesen, fn egyenletesen tart f-hez, de f nem deriválható mindenhol.
2. minden fn deriválható az egész számegyenesen, fn egyenletesen tart f-hez, f mindenhol deriválható, de f deriváltja nem egyezik meg a tagok deriváltjának határértékével.
|
| Előzmény: [248] Lóczi Lajos, 2006-02-14 21:35:16 |
|
| [248] Lóczi Lajos | 2006-02-14 21:35:16 |
 Ilyen tétel a deriválásra nemigen van, mivel az Általad írt állítás nem igaz. A tagok egyenletes konvergenciája még kevés. (HF: mutass ellenpéldákat.)
Egy elégséges feltétel például, ha fn egyenletesen tart f-hez, minden fn deriválható és fn' egyenletesen tart valamely g függvényhez, akkor f deriválható és deriváltja g.
|
| Előzmény: [246] nadorp, 2006-02-14 10:04:39 |
|
|
| [246] nadorp | 2006-02-14 10:04:39 |
 Egyenletes konvergencia esetén szabad. Van egy olyan tétel, hogy ha adott egy fn(x) függvénysorozat, és 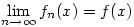 és a konvergencia egyenletes, akkor és a konvergencia egyenletes, akkor 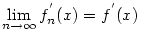 , azaz szabad tagonként deriválni. Ugyanez igaz integrálásra is. Az egyeneletes konvergencia nagyjából azt jelenti, hogy az |fn(x)-fm(x)| különbségek elég nagy n,m-re x-től függetlenül tetszőlegesen kicsik lesznek. , azaz szabad tagonként deriválni. Ugyanez igaz integrálásra is. Az egyeneletes konvergencia nagyjából azt jelenti, hogy az |fn(x)-fm(x)| különbségek elég nagy n,m-re x-től függetlenül tetszőlegesen kicsik lesznek.
Legyen most fn(x)=1+x+x2+...+xn, ahol x [-r;r] és 0<r<1. Ekkor, ha n>m, akkor [-r;r] és 0<r<1. Ekkor, ha n>m, akkor 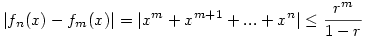 ,és ez tetszőlegesen kicsi (x-től függetlenül), ha m elég nagy. Tehát a ,és ez tetszőlegesen kicsi (x-től függetlenül), ha m elég nagy. Tehát a 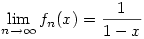 konvergencia egyenletes a [-r,r] intervallumon, ezért szabad tagonként integrálni. Hasonló a gondolatmenet, ha konvergencia egyenletes a [-r,r] intervallumon, ezért szabad tagonként integrálni. Hasonló a gondolatmenet, ha 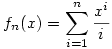 . Itt is igaz,hogy . Itt is igaz,hogy 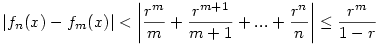 , tehát a függvénysorozat egyenletesen konvergál,ezért szabad tagonkét deriválni. , tehát a függvénysorozat egyenletesen konvergál,ezért szabad tagonkét deriválni.
|
| Előzmény: [245] rizsesz, 2006-02-14 00:59:22 |
|
| [245] rizsesz | 2006-02-14 00:59:22 |
 az eredmény biztosan jó, csak a nyitott kérdés érdekes a végén, miszerint lehet-e deriválni, majd az így kapott sorozaton elvégezve a szummázást, és azt visszaintegrálni ér-e :)
|
|
| [244] Mate | 2006-02-14 00:43:02 |
 Miért nem próbálod Taylor-sorba fejteni?
|
|
| [243] rizsesz | 2006-02-13 22:42:48 |
 sziasztok. igazából egy vicces igen-nem kérdésem lenne az analízis témaköréből. azt a feladatot kaptuk, hogy igazoljuk a sum (p ad i/i) i=1->végtelen=-ln(1-p) összefüggést (elnézést a TeXtelenségért továbbra is :S) a következő megoldást találtam ki:
-vegyük az általános tag deriváltját, ez a p ad i/i deriváltja p szerint, az p ad (i-1) -ha ezeket a deriváltakat összeadjuk, szóval 1+p+p ad 2+... p ad végt. összeget képezzük, az a végt. mértani sor összegképlet miatt 1/(1-p) -most a kezdeti deriválást visszacsinálva egy integrálással, pont megkapjuk a -ln (1/(1-p))-t :)
lényegében a kérdés annyi, hogy van egy csökkenő tagú sorozat, és ha az elemeket deriválom, és úgy végzem el az összegzést, majd visszaintegrálok, akkor az eredetivel megegyező összeget kapom-e meg?
segítségeteket előre is köszi, rizsa
|
|
|
|
|
| [239] hobbymatekos | 2006-02-05 01:24:04 |
 Még egy megjegyzés az exponenciális tag jogosságáról: lin. diffegyenletek esetén az exponenciális fv-ek alaprendszert alkotnak. Azaz kereshető a homogén egyenlet megoldása exp. fv ek lin. kombinációjaként.
|
| Előzmény: [198] Wolf, 2005-11-01 20:39:02 |
|
| [238] hobbymatekos | 2006-02-05 01:13:44 |
 Ez valójában egy rendszer egységugrás fv-re adott válaszaként értelmezhető,tehát az átviteli függvény. A Bode és Nyqist diagrammok adnak felvilágositást egy rendszer stabilitásáról. ( körfrekvencia és a komplex impedancia pl.)Egy rezgőkör pl. közönséges lineáris másodrendű diffegy.. Nos ezeknek a diagrammoknak az összehasolitása jóval könnyebb és a villamosmérnökök (is) azonnal látják belőle a rendszer állapotát.
|
| Előzmény: [198] Wolf, 2005-11-01 20:39:02 |
|
| [237] hobbymatekos | 2006-02-05 00:50:44 |
 Sziasztok. bizonyos diffegyenletek... nevezzük nevén: kizárólag lineáris közönséges diffegyenletekre és diffegyenletrendszerekre alkalmazható módszer, azaz ha érvényes a szuperpozició elve. Értelmezett a megoldás az abszolut konvergenciaabszcisszánál nagyobb t re illetve diffegyenletrendszerek esetén a konvergenciaabszisszák által meghatározott intervallumok közös részén.Ott és csakis ott. Az abszolút konvergenciaabszcissza meghatározása Stjieltjes integrál. Gyakran nehéz kiszámolni... Egyébként értelmezhető negativ valósra értelmezett fv-re is a Laplace transzformált (baloldali-nak nevezzük). Viszont az alkalmazások zöme valóban villamosmérnöki (teljesitményelektronika).... DE: a legszebb talán a szabályozástechnika (felnyitott hurok átviteli fv-e, differenciáló és integráló tagok...Itt éppen a differenciálás ás integrálás egyszerüsége az előny). Az AHA élmény ekkor szokott ennél a transzformációtipusnál általában jelentkezni... DE az inverz L trafó létezése és annak konvergenciája bizonyitásra szorul... és szintén nem könnyü...
|
| Előzmény: [209] Lóczi Lajos, 2005-11-04 20:46:17 |
|
| [236] joe | 2006-01-30 20:42:55 |
 (önkényesen jelölést változtatva: az x2 - kbx + b2 - k = 0 egyik gyöke a, a másik legyen c; f(x, y) := (x2 + y2) / (1 + xy)); ekkor ha f(a, b) = k, akkor f(b, c) = k. Az könnyen látható, hogy (egyrészt c nem= b, másrészt) b > c (ezt elég arra az esetre belátni, ha a > b > 0). A gyökök és együtthatók közti összefüggésekből c = kb - a. Így egy rekurzív sorozathoz jutunk, aminek (mivel 2 kezdőtagja és a k egész) mineden tagja egész. A sorozat szig. fogyó (ezt elég az első nempozitív tagig belátni); így egyszer eljutunk olyan a > b -hez, melyre f(a, b) = k ("mint mindig"), és a > 0 >= b. Ekkor, mivel f(a, b) számlálója pozitív, és értéke is pozitív (k), így a nevező is az, ezért ab > -1. Mivel a, b egészek, ez csak úgy lehet, ha b = 0. Ekkor viszont k = f(a, b) = f(a, 0) = a2; qed. (bocsánat, hogy még mindig nem tudok TeXelni)
|
| Előzmény: [235] Kós Géza, 2006-01-20 11:13:59 |
|
| [235] Kós Géza | 2006-01-20 11:13:59 |
 Egy kis segítség.
Legyen k egy olyan egész szám, ami előáll a kívánt alakban:
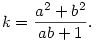 | (1) |
Vizsgáljuk most a következő másodfokú egyenletet:
Ennek az egyik gyöke x1=b.
Mit mondhatunk a másik gyökről?
|
| Előzmény: [230] Sirpi, 2006-01-18 17:33:26 |
|
|
| [233] Kós Géza | 2006-01-18 20:25:22 |
 Amit írtam, az nem ellenpélda, hanem példa akart lenni. Ezek szerint én voltam félreérthető.
Az egész értékek között minden pozitív négyzetszám végtelen sokszor előfordul. (Megoldást azért nem írok, mert ismerem a feladatot.)
|
| Előzmény: [232] Sirpi, 2006-01-18 19:04:29 |
|
| [232] Sirpi | 2006-01-18 19:04:29 |
 Géza, ezt nem teljesen értem, mire írtad, ez egy példa, amikor a tört értéke tényleg négyzetszám. Azt kell bizonyítani, hogy nincs olyan a és b, amikor a tört egész, és a tört értéke mégse négyzetszám (bocs, ha eredetileg félreérthetően fogalmaztam).
|
| Előzmény: [231] Kós Géza, 2006-01-18 17:54:52 |
|
|
| [230] Sirpi | 2006-01-18 17:33:26 |
 137. feladat.: bizonyítsd be, hogy ha a és b természetes számok és 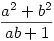 egész, akkor négyzetszám is egyúttal (nemrég hallottam, nem tudom a megoldást, de van 1-2 részeredményem). egész, akkor négyzetszám is egyúttal (nemrég hallottam, nem tudom a megoldást, de van 1-2 részeredményem).
|
|





 [-r;r] és 0<r<1. Ekkor, ha n>m, akkor
[-r;r] és 0<r<1. Ekkor, ha n>m, akkor 
