| [555] Lóczi Lajos | 2007-07-03 20:00:17 |
 Sőt, az is igaz, hogy ha egy polinom minden együtthatója algebrai szám, akkor a gyökei is algebraiak. Ennek speciális eseteként rögtön adódik a válasz a kérdésre.
|
| Előzmény: [548] Cckek, 2007-07-02 14:42:48 |
|
|
| [553] Enkidu | 2007-07-03 17:11:25 |
 Sziasztok!
Ha a gyöke egy k-adfokú p(x) racionális együtthatós polinomnak, akkor p(x) = (x - a)(x - a2)...(x - ak). Ekkor a következő kn-edfokú q(x) szintén racionális együtthatós polinomnak 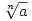 (persze az összes koplex gyök is) a gyöke: q(x) = (xn - a)(xn - a2)...(xn - ak) Innentől Jonas bizonyítja a hátralévő (persze az összes koplex gyök is) a gyöke: q(x) = (xn - a)(xn - a2)...(xn - ak) Innentől Jonas bizonyítja a hátralévő 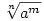 részt:). részt:).
Bocs az esetleges rossz képletekért még át kell néznem a TeX-et. Sziasztok
|
| Előzmény: [548] Cckek, 2007-07-02 14:42:48 |
|
|
| [551] jonas | 2007-07-03 12:48:49 |
 Igen, az algebrai számok résztestet alkotnak a valós vagy komplex számokban, de ezt nem elemi módon lehet könnyen bizonyítani, hanem algebrával. Ha kell a bizonyítása, akkor a régi algebra 1 vagy 2 füzeteimben utánanézhetek.
|
| Előzmény: [548] Cckek, 2007-07-02 14:42:48 |
|
| [550] jonas | 2007-07-03 12:46:34 |
 Szerintem ez nagyágyú ehhez. Egyszerűen mondhatjuk azt, hogy létezik transzcendens szám (mondjuk az e) és nyilván bármely x transzcendens számra és a racionális számra x+a is transzcendens, így pedig bármely intervallumba bele lehet tolni az e-t.
|
| Előzmény: [549] Lóczi Lajos, 2007-07-02 15:55:25 |
|
|
|
| [547] Cckek | 2007-07-02 14:03:48 |
 Minden nyílt intervallum tartalmaz transzcendens számokat. Kiváncsi vagyok az ötleteitekre.
|
|
|
| [545] xviktor | 2007-06-13 11:28:33 |
 Hali!
Paros fuggvenyeknel grafikus abrazolasban az y tengelyre szimmetrikus. (x tengelyre csak a konstans 0 az, egyebkent nem lenne fuggveny) :-)
Udv: Viktor
|
| Előzmény: [544] mrmorotz, 2007-06-13 11:22:29 |
|
| [544] mrmorotz | 2007-06-13 11:22:29 |
 A páros függvény olyan függvény, amelyre f(-x) = f(x) , minden x eleme Df-re. GRafikusan azok a páros függvények, amelyek képe szimmetrikus az x tengelyre. Például az x*x fv. ilyen. Páratlan: f(-x)=-f(x). Az ilyen fv. grafikonja szimmetrikus az origóra. Lásd köb(x).
|
| Előzmény: [536] amynna, 2007-06-08 17:35:28 |
|
|
|
| [541] amynna | 2007-06-09 19:34:13 |
 Én is most vettem észre, hogy 1/b feladatot tényleg elnézted, mert én minuszt irtam. sehogy nem jött ki a nekem az eredmény. megpróbálom mégegyszer felrakni, nagyon örülnék, ha tudnátok segiteni és nemcsak az eredményt irnátok le, hanem a levezetést is. Nagyon köszönöm. Franciska
|
| Előzmény: [540] Sirpi, 2007-06-09 11:55:35 |
|
| [540] Sirpi | 2007-06-09 11:55:35 |
 Igen, a gyökös feladatot elnéztem, kétszer is: egyrészt rosszul olvastam el a feladatot, másrészt a meg a rossz feladatra is elírtam a megoldást, köszi a helyreigazítást :-)
|
| Előzmény: [538] Fálesz Mihály, 2007-06-09 06:35:21 |
|
| [539] Fálesz Mihály | 2007-06-09 06:42:14 |
 Az azért mindig relatív, hogy milyen problémák a nehezebbek...
| ... Erre apukám megint elmondta, hogy őt nem érdekli, hogy más gyereke mit csinál, de nagyon szégyellte magát helyettem a tanító néni előtt. Sajnáltam apukámat, hogy helyettem szégyellte magát, mert szégyellni már én is tudom magamat a tanító néni előtt, csak szép kövér karikákat nem tudok még egyedül rajzolni. (Janikovszky Éva: Velem mindig történik valami) |
|
|
| Előzmény: [537] Sirpi, 2007-06-09 00:34:36 |
|
|
| [537] Sirpi | 2007-06-09 00:34:36 |
 Zárójel-fóbiád van? :-) Csak mert nem tettél ki egyet sem, pedig látható, hogy rengeteg helyre kellett volna. És ez eléggé egy (nem is túl nehéz) gyakorló feladatsornak tűnik, gondolom nem sok haszna lenne, ha tálcán kapnád az összes megoldást, ezért első körben tényleg inkább csak rávezetést adnék, ahogy írtad is az egyik hsz-edben korábban (kivéve a deriválós példáknál, ott egyszerűen nem tudtam a végeredmény leírása nélkül segíteni - ott próbáld meg Te is kiszámolni a deriváltat és vesd össze a két eredményt)
1a) emelj ki az 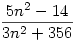 törtből n2/n2-et, és ekkor már elég könnyű látni, hogy a megmaradó tört hova tart. törtből n2/n2-et, és ekkor már elég könnyű látni, hogy a megmaradó tört hova tart.
1b) emeljünk ki a 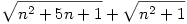 kifejezésből kifejezésből 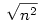 -et, és használjuk ki, hogy n2+5n+1=(n+5/2)2-21/4. -et, és használjuk ki, hogy n2+5n+1=(n+5/2)2-21/4.
2a) f'(x)=20x3-x-1/2-6.x-3
2b) f'(x)=3x2cos x-x3sin x
2c) gondolom itt az 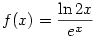 fv.-ről van, szó (bár a leírás nem könnyíti meg a helyzetem), ez esetben f'(x)=(1/x-ln 2x).e-x fv.-ről van, szó (bár a leírás nem könnyíti meg a helyzetem), ez esetben f'(x)=(1/x-ln 2x).e-x
3) 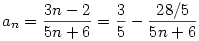 . Ebből nyilvánvaló, hogy a sorozat korlátos (hiszen monoton növekszik), és határértéke 3/5. . Ebből nyilvánvaló, hogy a sorozat korlátos (hiszen monoton növekszik), és határértéke 3/5.
4) f páros, ha f(x)=f(-x), páratlan, ha f(x)=-f(-x) minden x-re. A beírt (helyesen f(x)=x2/(1+x2)) függvény két páros függvény hányadosa, tehát páros.
Amúgy ezek a feladatok sokkal inkább az ujjgyakorlatok, mintsem a nehezebb matematikai problémák tárgykörébe tartoznak...
|
| Előzmény: [536] amynna, 2007-06-08 17:35:28 |
|
| [536] amynna | 2007-06-08 17:35:28 |
 ime: 1.) Számitsuk ki a sorozatok határértékét:
a./ an= 5n2-14n/3n2+356n b./ an= gyökjeln2+5n+1-gyökjeln2+1
2.) deriválni kell a függvényeket. a.) f(x)= 5x4-2gyökjelx +3/x2 b.) f(x)= x3. cosx c.) f(x)= ln2x/ex
3.) be kell bizonyitani a sorozat korlátosságát, monitását
an= 3n-2/ 5n+6
4.) Mikor mondjuk, egy függvényről, hogy páros ill.páratlan? paritás vizsgálat: f(x)=x2/1+x2
|
|
|
|
| [533] nadorp | 2007-06-08 13:59:10 |
 1. F(x)=3x3-2x2+5x-1
F'(x)=9x2-4x+5
F''(x)=18x-4
Ott lehet szélsőérték,ahol F'(x)=0. Mivel a másodfokú egyenlet diszkriminánsa negatív és F'(x) főállású parabola, ezért F'(x)>0, tehát F(x) szigorúan monoton növekvő.
2. f(x)=xln x
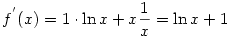 felhasználtuk, hogy (fg)'=f'g+fg' felhasználtuk, hogy (fg)'=f'g+fg'
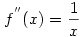
Ott lehet szélsőérték, ahol f'(x)=ln x+1=0, tehát 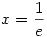 . .
Ha 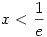 , akkor f'(x)<0, a függvény csökken , akkor f'(x)<0, a függvény csökken
Ha 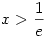 , akkor f'(x)>0, a függvény nő , akkor f'(x)>0, a függvény nő
A fentiekből következik, hogy 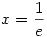 -ben minimum van -ben minimum van
3.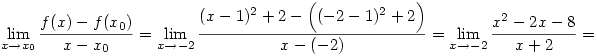
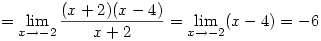
|
| Előzmény: [531] amynna, 2007-06-08 12:37:21 |
|
| [532] amynna | 2007-06-08 13:03:02 |
 Hú nagyon fontos, hogy valaki rávezessen..::!!!
|
|
| [531] amynna | 2007-06-08 12:37:21 |
 Na akkor mégegyszer, egy kis segitség kellene anal.ból...
A függvényen el kell végezni a monotonitás és szélsőérték vizsgálatot és meg kell adni a függvény második deriváltját is. F(x)=3x3-2x2+5x-1 sajna nem tudom helyesen jelölni a függvényt, de ezt ti értitek, hogy a harmadikon, másodikon... ez is kellene , f(x)=xlnx
másik példa: a differenciálhányados definiciójára épitve ki kellen számitani az f(x)=(x-1)2+2 függvény xo/null/=-2 helyen vett differenciálhányadosát.
|
|






 Q[X] polinomnak akkor
Q[X] polinomnak akkor  q
q
