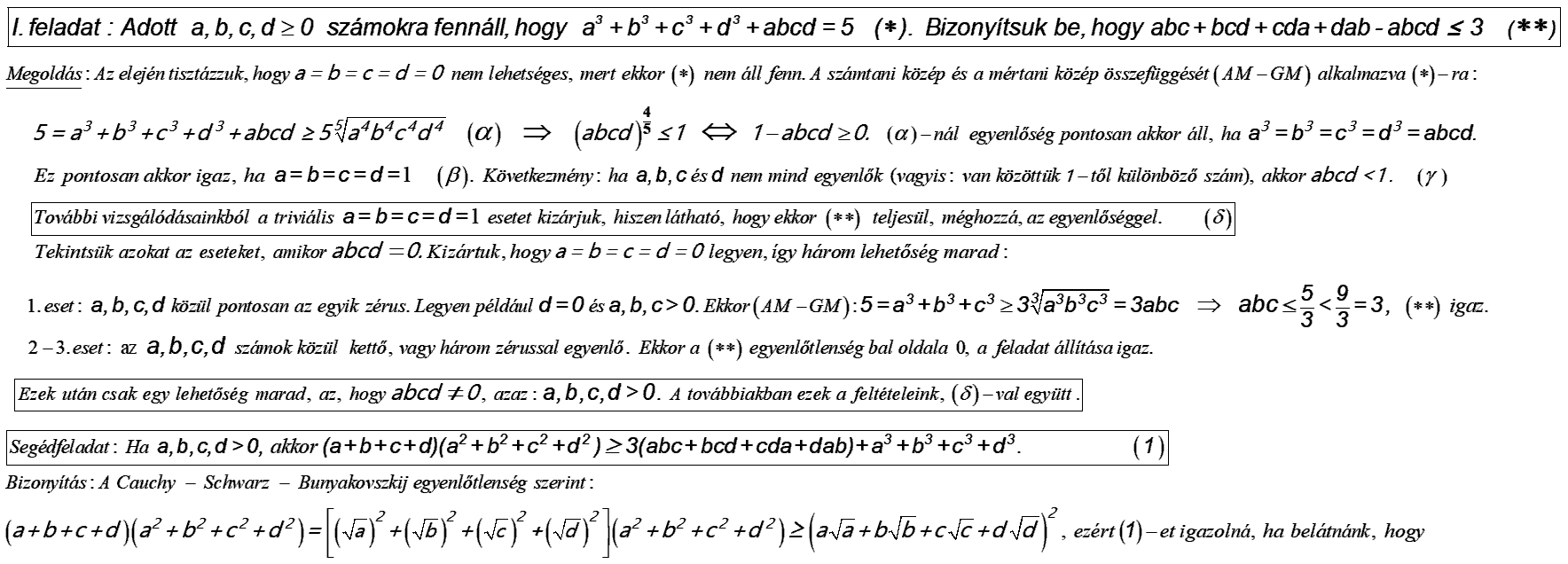|
| [833] sakkmath | 2019-10-31 18:10:42 |
 A megoldáshoz messzebbről kellett elindulnom (I.feladat). Ennek eredményeit felhasználva sikerült igazolnom az eredeti, itt II. feladatot.
Egységes szerkezetbe foglalva tehát erről a két problámáról van szó:
Adottak az a,b,c,d nemnegatív valós számok, melyekre a3+b3+c3+d3+abcd=5. Bizonyítsuk be, hogy:
I.:abc+bcd+cda+dab−abcd≤3,
II.:ab+cd≤2.
Lényegében sikerült "csak" nevezetes egyenlőtlenségekkel dolgozni, de ennek sajnálatos ára lett a hosszú levezetés. Nem vagyok TEX-mester, így a megoldást csak 4 darab GIF-kép beszúrásával tudom prezentálni, melyek négy hsz.-t igényelnek. ( Nem találom azt a hsz.-t, amelyben régen valaki leírta, hogy neki milyen trükkökkel sikerült több képet elhelyezni egy hozzászólásban. Kár, hogy ez a módszer azóta sem került be a TEX minitanfolyamba!).
Következzék tehát a megoldás, négy (remélhetőleg) egymást követő hozzászólásban.
Az 1. rész:
|
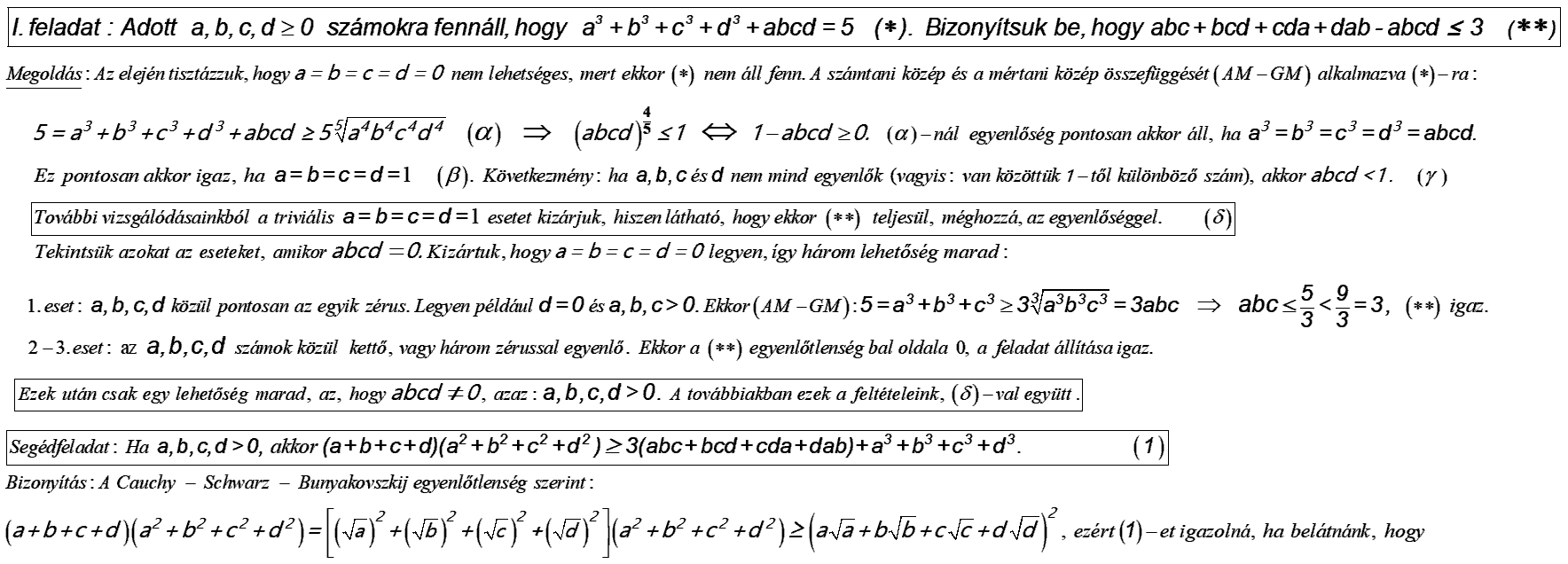 |
| Előzmény: [822] sakkmath, 2019-07-10 12:30:18 |
|
| [832] Berko Erzsebet | 2019-08-17 10:49:22 |
 Mire jutottam Twin1 és Twin2-vel? (a*b+c*d)*(a*b+c*d)<=(a*a+c*c)*(b*b+d*d). De ez sitty-sutty jön a Cauchy-Schwarz-Bunyakovszkij-egyenlőtlenségből (a;c) illetve (b;d)-re alkalmazva. Más. Aztán még van ezem: a*b+c*d<=(a+c)*(b+d), mert a jobb oldalon a szorzást elvégezve több tag van, mint a bal oldalon.
|
| Előzmény: [830] sakkmath, 2019-08-16 09:23:52 |
|
|
| [830] sakkmath | 2019-08-16 09:23:52 |
 Az észrevétel jogos, egyetértek, köszönöm. Sajnos ellenőrzés nélkül vettem át a cut-the-knot sajtóhibás közlését, ezer bocsánat.
Úgy látom, hogy a Twin1 oldalának behívása után a "Problem"-ben is és a "Solution 1"-ben is, az egyenlőtlenség bal oldalán, (ab+cd)2 -et kell szerepeltetni a téves (ac+bd)2 helyén.
Ennek megfelelően, a [828]-ban általam felírtak helyére ez lép:
(ab+cd)2≤(b5√ab4+d5√cd4)(a5√a4b+c5√c4d).
Remélem, most nem tévedtem. Ha mégis, visszajelzést kérek.
|
| Előzmény: [829] Berko Erzsebet, 2019-08-15 16:48:00 |
|
| [829] Berko Erzsebet | 2019-08-15 16:48:00 |
 Úgy látom, hogy a felírt egyenlőtlenség nem igaz. Bocsánat, ha tévedek. Néztem az a=0,1, b=0,2, c=0,3, d=0,4 helyettesítést. Erre nem teljesül. Elkezdtem nézni Twin1-et (bár ez a Cauchy-Schwarz-(B)-egyenlőtlenség egy alkalmazása, ahogy olvasható is), Solution1-ben található helyettesítéseket megcsináltam, de nekem a bal oldalon a*b+c*d van a*c+b*d helyett. Ekkor gondoltam megnézek egy számnégyest. Még egyszer bocsánat, ha én néztem el valamit.
|
| Előzmény: [828] sakkmath, 2019-08-14 21:05:38 |
|
| [828] sakkmath | 2019-08-14 21:05:38 |
 Egy új megoldás kiindulópontja lehet a 4 változóra felírt Twin1 inequalities itt. Jelen feladatra rímelő változata:
Ha a,b,c,d>0,akkor
(ab+cd)2≤(c5√ac4+d5√bd4)(a5√a4c+b5√b4d).
(Van egy névrokona is emitt.)
|
| Előzmény: [822] sakkmath, 2019-07-10 12:30:18 |
|
| [827] Berko Erzsebet | 2019-08-13 20:50:31 |
 Igyekeztem átnézni. Tehát felhasználtad a Jensen-egyenlőtlenséget is. Illetve felcsillant a szemem egy számnál: 2*(5/4)(2/3). Ez kb. 2,32079... Ez nekem is kijött közepekkel, augusztus 2-án írtam is erről. Írtam a 2,32-ről.
|
| Előzmény: [826] nadorp, 2019-08-13 17:45:19 |
|
| [826] nadorp | 2019-08-13 17:45:19 |
 "Ez a háromszög tartalmazza a másik szimmetrikus tartományt".
Ez azért még nem bizonyítás, hogy 5 pont berajzolása után "látszik" :-)
Teljesen középiskolait nem találtam, egy kis függvényvizsgálattal a Te ötleteddel a megoldás befejezhető.
Vezessük be az x+y=p változót és fix p mellett az x∈[0;p] intervallumon definiáljuk az fp(x) (nem parciális deriválás!) függvényt a következőképpen:
fp(x)=2x32+2(p−x)32+x(p−x)
Tudjuk, hogy létezik olyan x, melyre fp(x)≤5
Az x32 függvény konvex, ezért
5≥2x32+2(p−x)32≥4(x+p−x2)32=4(p2)32
Ebből következik, hogy p<3 biztosan teljesül.
Most belátjuk, hogy az fp(x) függvénynek az x=p2 helyen abszolút minimuma van
f′p(x)=3√x−3√p−x+p−2x=3(2x−p)√x+√p−x+p−2x=(2x−p)(3√x+√p−x−1)
A √x függvény konkáv, ezért
√x+√p−x≤2√x+p−x2=√2p, azaz
3√x+√p−x−1≥3√2p−1>3√6−1>0
Az kaptuk, hogy
f′p(x){<0 ha x<p2=0 ha x=p2>0 ha x>p2
Ebből következik, hogy az fp(x) függvénynek az x=p2 helyen abszolút minimuma van,tehát p összes lehetséges értékére fp(p2)≤5
p√2p+p24≤5
A fenti egyenlőtlenség p=2 esetén egyenlőséggel teljesül és mivel a bal oldal p-ben szigorúan monoton növekvő, ezért valóban p≤2.
|
| Előzmény: [825] Berko Erzsebet, 2019-08-09 15:49:12 |
|
| [825] Berko Erzsebet | 2019-08-09 15:49:12 |
 Sikerült csinálnom egy középiskolai ismereteket felhasználó bizonyítást. Remélem. Kell hozzá a számtani és mértani közepekre vonatkozó egyenlőtlenség, meg van benne koordináta-rendszer. Talán, ha a koordináta-rendszeres rész algebrai lenne, akkor értékesebbnek tartanám a bizonyítást.
Tehát a(3)+b(3)+c(3)+d(3)+a*b*c*d=5, ahol 0<a, b, c, d<1,709...(köbgyök5). Kell: a*b+c*d<=2. Bizonyítás.Látszik könnyen, hogy a=b=c=d=1-re a*b+c*d=2. A>=G miatt (a(3)+b(3))/2>= sqrt(a(3)*b(3)), innen a(3)+b(3)>=2*((a*b)(1,5)). Hasonlóan c(3)+d(3)>=2*((c*d)(1,5)). 5>=2*((a*b)(1,5))+2*((c*d)(1,5))+a*b*c*d Bevezetek 2 új ismeretlent, változót: a*b=x, c*d=y. Ezekkel 5>=2*x(1,5)+2*y(1,5)+x*y (1). Kell:x+y<=2 (2). Innen koordináta-rendszer segítségével megy a bizonyítás. (1) képe egy szimmetrikus tartomány. Néhány pontja: (0;0), (1;1), (2,5(2/3);0), (0; 2,5(2/3)).(2,5)(2/3) kb. 1,8420. Majd berajzoltam az y<=-x+2-nek eleget tevő pontokat, 2 egység oldalú egyenlő szárú derékszögű háromszög. Ez a háromszög tartalmazza a másik szimmetrikus tartományt. Sok-sok látszólag sehova se vivő(?)számolás után ezt most gyorsan összeraktam, leírtam. Lehet, hogy jobb lett volna aludni rá egyet... (a(3)=a*a*a, (a*b)(1,5)= alap: a*b, kitevő: 3/2)
|
| Előzmény: [824] sakkmath, 2019-08-05 19:03:55 |
|
| [824] sakkmath | 2019-08-05 19:03:55 |
 Bár régóta ismerem és küzdök vele, csak ma tudtam megoldani (!) a feladatot - kizárólag középiskolai ("Lagrange-mentes") ismeretanyagra támaszkodva. (A Lagrange-féle multiplikátor-módszer persze jó volt az előzetes ellenőrzésre … .)
Remélem, beérkezik majd egy-két érdekes megoldás. Ezt követően, összehasonlítás céljából, én is feltenném a sajátomat.
Köszönöm, hogy foglalkoztál/foglalkozol a feladattal.
|
| Előzmény: [823] Berko Erzsebet, 2019-08-02 10:09:51 |
|
| [823] Berko Erzsebet | 2019-08-02 10:09:51 |
 Elő-előveszem a feladatot. Közepekkel... még nem sikerült belátnom 2-re, csak 2,32 körülire. Mivel ez egy feltételes szélsőérték probléma, segít a Lagrange-féle multiplikátor-módszer. Azzal kijön. Felírjuk a Lagrange-függvényt, majd meghatározzuk az elsőrendű parciális deriváltakat, amiket egyenlővé teszünk nullával...Azt is megfigyeltem, hogy a számok összege (a, b, c, d) nem lehet 4-nél több.
|
| Előzmény: [822] sakkmath, 2019-07-10 12:30:18 |
|
| [822] sakkmath | 2019-07-10 12:30:18 |
 Adottak az a,b,c,d nemnegatív valós számok, melyekre a3+b3+c3+d3+abcd=5. Bizonyítsuk be, hogy:
ab+cd≤2.
|
|
| [821] csábos | 2017-03-09 20:56:56 |
 A módszert úgy hívják, hogy rezultáns. A WOLFRAMALFA Res függvénye. Az jön ki, hogy az x:y:z arány épp a (x3+(6−√3)x2−4√3x−1) gyökei. Egy hasonló feladat volt régebben. Megjegyzendő, hogy (x3+(6−√3)x2−4√3x−1)(x3+(6+√3x2+4√3x−1)=x6+12x5+33x4−26x3−60x2+1.
Ennek szellemében tudunk valami szép megoldást:
|
| Előzmény: [820] jonas, 2017-03-09 16:13:27 |
|
| [820] jonas | 2017-03-09 16:13:27 |
 Yield már olyan alakra hozta, ahol két kétváltozós valós másodfokú egyenletnek kell a közös gyökét keresni. Ilyen egyenletrendszerre van általános egzakt megoldás, négyzetgyökökkel, de ez kevéssé ismert. Ha viszont a gyakorlatban találkozol egy ilyen egyenletrendszerrel, és akár szimbolikus megoldást keresel, akár megbízható numerikusat, nem könnyű meglévő szoftver implementációt találni. A Wolfram Alpha érthető befejezés volt.
|
| Előzmény: [819] Róbert Gida, 2017-03-09 15:07:09 |
|
| [819] Róbert Gida | 2017-03-09 15:07:09 |
 Akkor tulajdonképpen a Wolfram Alpha oldotta meg a problémát: Wolfram
itt a második alternatív alaknál nullára rendezte és felírja u*conj(u) alakban a kifejezést, én csupán ezt az alakot gyöktelenítettem. A Reduce[]-ra egyébként True-t ír, azaz ténylegesen be tudja bizonyítani az egyenlőtlenséget valós x,y,z-re.
A megoldásodból az is látható, hogy nemnegatív valós x,y,z-re egyenlőség csak a trivi x=y=z esetben van.
|
| Előzmény: [818] yield, 2017-03-09 10:43:05 |
|
| [818] yield | 2017-03-09 10:43:05 |
 Feladat sokkal nehezebb része Róbert Gida elvégezte! Bridge játéknál azt mondják, hogy "a lordok licitálnak a szolgák lejatsszák az osztást".
Egyenlőség akkor van ha "u" valós és képzetes része = 0
1. Ha z = 0, akkor csak x = y = 0 lehet.
2. Ha z <> 0, akkor egyenletek homogén alakja miatt behelyettesíthető a = xz, b = yz. Két egyenletünk Wolframalphának beadva: link
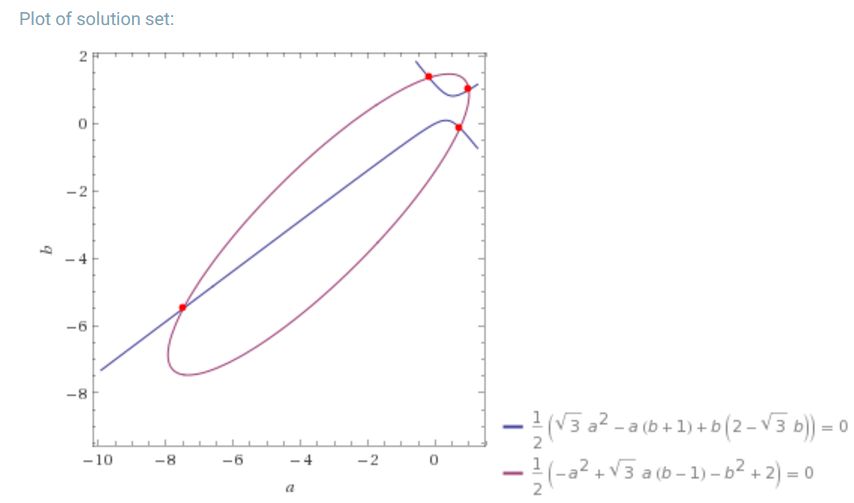
Négy megoldás van:
(xz,yz) = (a,b) = (1,1), (-7.48085, -5.49553), (-0.181966, 1.36126), (0.734614, -0.133675)
|
 |
| Előzmény: [817] csábos, 2017-03-08 20:43:16 |
|
|
| [816] Róbert Gida | 2017-03-07 23:26:59 |
 Legyen f(x,y,z)=x4+y4+z4+(√3−1)xyz(x+y+z)−√3(x3y+y3z+z3x), kell f(x,y,z)≥0. Belátom, hogy f(x,y,z) éppen egy komplex szám abszolútértékének a négyzete, így nemnegatív. Legyen S=√3 és E=1+iS, ekkor f(x,y,z)=|u|2, ahol: u=12ESx(ix−z)−34yE2(ix+y)+iyz+z2.
|
| Előzmény: [815] csábos, 2017-03-06 23:44:09 |
|
| [815] csábos | 2017-03-06 23:44:09 |
 Kitaláltam egy feladatot. Tud valaki rá jobbfajta megoldást?
Bizonyítsuk be, hogy
(x4+y4+z4)+(√3−1)xyz(x+y+z)≥√3(x3y+y3z+z3x)
Mikor áll fönt egyenlőség?
|
|
| [814] nadorp | 2017-02-01 23:59:18 |
 Egy kiegészítés.
Bebizonyítjuk, hogy ha f′(t)=f(f(t)) teljesül minden valós t-re, akkor létezik f-nek fixpontja. Ebből már következik, hogy a [813]-ban megadott linken levő Taylor-sor család megadja az összes megoldást.
Tegyük fel, hogy f-nek nincs fixpontja. Ekkor vagy f(t)−t>0 vagy f(t)−t<0 teljesül minden valós számra, hiszen f folytonos is.
1.eset: f(t)>t
Legyen t≥0. Ekkor f(t)>t≥0 miatt f(f(t))>f(t) is teljesül, azaz
Ebből egyrészt következik hogy t≥0 esetén f(t) szigorúan monoton nő, tehát t≥f(0)>0 esetén f-nek létezik egyértelmű f−1(t)≥0 inverze. Az eredeti egyenletet ezzel felírva
f′(f−1(t))=f(t)
Másrészt (1) mindkét oldalát megszorozva e−t-vel és rendezve
(f′(t)−f(t))e−t>0
(f(t)e−t)′>0
Tehát az f(t)e−t függvény t≥0 esetén szigorúan monoton nő, így
f(t)e−t≥f(0)
Összevetve (2)-t és (3)-at t>f(0)>0 esetén kapjuk, hogy
(f−1)′(t)≤1f(0)e−t
∫tf(0)(f−1)′(s)ds≤1f(0)∫tf(0)e−sds
f−1(t)≤1f(0)(e−f(0)−e−t)<e−f(0f(0)
Ez viszont ellentmondás, mert t>f(0)>0 esetén f−1(t) nem lehet korlátos.
2.eset: f(t)<t
Legyen t≤0. Ekkor f(t)<t≤0 miatt f(f(t))<f(t) is teljesül, azaz
f′(t)<f(t)<0
Ebből következik hogy t≤0 esetén f(t) szigorúan monoton csökken.
Legyen most a=f(0)<0. Ekkor a monoton csökkenést felhasználva
f(a)>f(0)=a>f(a)
Ez pedig ellentmondás.
|
| Előzmény: [813] nadorp, 2017-01-28 09:05:15 |
|
| [813] nadorp | 2017-01-28 09:05:15 |
 Elindultam abból, hogy keressünk olyan megoldást, ahol létezik a, hogy f(a)=a. Eljutottam az f(f(x)) függvény n-dik deriváltjának a képletéig, ami alapján elkezdtem Taylor-sorba fejteni f-et a fixpont körül, felhasználva a Faà di Bruno Formulát. Ez előbb-utóbb elég csúnya lesz, ezért rákerestem a neten (hátha...) és ezt találtam, ami megfelel a fenti gondolatmenetnek ( az utolsó hozzászólás a lényeges):
lásd itt
|
| Előzmény: [812] Sinobi, 2017-01-26 00:58:28 |
|
| [812] Sinobi | 2017-01-26 00:58:28 |
 Milyen f függvények vannak, amelyeknek a deriváltjuk megegyezik az ismételtjükkel, azaz: f′(t)=f(f(t))?
Ezt, vagy az ilyesmiket hogyan kell/lehet?
|
|
|
| [810] yield | 2017-01-07 19:40:51 |
 Ha felírjuk a koszinusztételt erre a háromszögre, akkor kapunk egy egyenletet q-ra. Ennek csak q =1 esetén lesz megoldása az alábbi állítás alapján: "Tegyük fel, hogy a (m/n) már nem egyszerűsíthető tört gyöke az f egész együtthatós polinomnak. Ekkor a számláló osztja f konstans tagját, a nevező pedig a főegyütthatóját"
|
| Előzmény: [809] marcius8, 2017-01-04 12:56:03 |
|