Fórum: Héttusa feladatok

Ez alapján 3 "szabad" rácspontunk van, amit nem muszáj lefednünk. Így nem lehet minden sarok üres, mert az 4 nem lefedett rácspontot jelentene. Nem lehet mind a 4 sarokban egymást átlósan ütő király-pár, mert az is 4 plusz rácspontot igényelne. 0 vagy 2 olyan király lehet, amelyik nem üt másikat, hiszen egy király önmagában 4 rácspontot foglal el. Ezek alapján kell legyen egy olyan sarok, amelyben két király oldalszomszédos mezőn áll. Forgatással és tükrözéssel megoldható, hogy ezek a bal felső sarokban az első sorban álljanak. Ha ehhez hozzávenném, hogy nyilvántartsam a "kihagyott" rácspontokat, akkor a program valószínűleg záros határidőn belül lefutna.

Másik ötlet a fentiek alapján, hogy a király-párokat igyekszem lerakni. Alapvetően nem sok eset lehet:

1. Minden pár oldalszomszédos: 3 rácspont marad ki.

2. Két egyedülálló király van (mint pl. a 27-es hozzászólásban), a többi oldalszomszédos: 1 rácspont marad ki.

3. Két egyedülálló király van, egy átlósan ütő pár, a többi oldalszomszédos: nincs kimaradó rácspont.

4. Egy, kettő vagy három átlósan ütő pár van, a többi oldalszomszédos: 2, 1 vagy 0 rácspont marad ki.

Mivel főleg király-párokat helyezünk el, a vizsgálandó esetek száma óriásit csökken, ez szerintem másodperceken belül meg kell adja az összes megoldást, bár leprogramozni bonyolultabb (valakinek nincs kedve megcsinálni? :) ). Amúgy szerintem a 3. pont és a 4. pontból az utolsó kettő nem fog előfordulni.

Kiszűrtem a forgatással/tükrözéssel egymásból megkapható megoldásokat és pár perc futás után találtam 156 megoldást. A programom nem nézte végig (valószínűleg ebben a formában nem is tudja végignézni) az összes lehetséges megoldást, így nem tudom, hogy ez mennyire van "közel" az összeshez...

Bocsi, zűrös volt az utóbbi pár nap, csak most olvastam. És igen, erre gondolt a költő... :)

Miért nem lehet 26-nál több királyt elhelyezni a táblán?

Figyeljük az "elfoglalt" rácspontokat.

A sakktáblán a rácsegyenesek $\displaystyle 9\cdot9=81$ pontban metszik egymást, 81 rácspont van.

2 egymást ütő király 6 vagy 7 rácspontot foglal el. Ha 2 másik ilyen királyt nézünk, azokhoz más rácspontok tartoznak. Ha a 26 király 13 párt alkot (az egy párban lévők ütik egymást), akkor ők legalább $\displaystyle 13\cdot6=78$ rácspontot foglalnak el a 81-ből ...

Ha jól számolom, már nyolc megoldásnál tartunk e kettővel együtt:

Ismét javítom magam (bocs).

E sor helyett ez a végleges szövegem:

"... ez a "Héttusa feladatok" - fórum / [22]-es hsz. / 3. kérdés / b. feladat."

Ebből könnyű volt megkapni a következő megoldást:

Persze ez a Héttusa számozása szerint a 3/b. feladat.

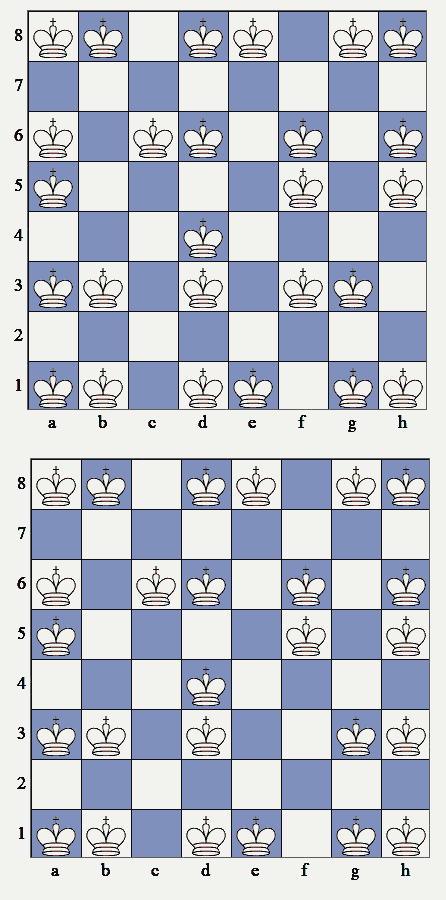
Újabb két megoldás alul.

24/b. feladat:

Hány különböző megoldása van a feladatnak, ha eltekintünk a (tengelyes-, vagy középpontos) tükrözésekből adódó többletmegoldásoktól?

De talán ez a legjobb, mert a mintázat könnyen bővíthető minden $\displaystyle 6k+2$ oldalú táblára. Sőt, minden páros $\displaystyle n$-ről $\displaystyle (n+6)$-ra.

Van még egy másik is

Szerintem erre gondolt a kolto:

Ka1,Kb1,Kd1,Ke1,Kg1,Kh1,

Ka3,Kb3,Kd3,Ke3,Kg3,Kh3,

Ka5,Kb5,Kd5,Ke5,Kg5,Kh5,

Ka7,Ka8,Kc7,Kc8,Kf7,Kf8,Kh7,Kh8

Soraidból sajnos nem tudom egyértelműen beazonosítani a programod megoldását/megoldásait. Örülnék, ha ezt/ezeket vagy ábrán, vagy koordinátázva bemutatnád, vagy leírnád.

A 3. kérdésre egy program 26-ot mondott: 2 soronkent vízszintesen 3 pár, az utolsó 2 sorban pedig függőlegesen 4 pár. Még "elméletben" bizonyítani nem tudom...

A lövős analógia a futókra is használható. A sarkokat ferdén levágjuk, így lesz 28 falszakasz. A többi szélső mezőről (24) legalább 1 falszakasz látható, a többi mezőről már 4-felé lehet lőni, ami már bábunként 2-2 új falszakaszt jelent. És a 4 sarokfalat lehet is támadni 1-1 átlómezőről.

Újabb kérdések:

3. kérdés: Legfeljebb hány király állhat a sakktáblán, ha mindegyik legfeljebb egy másikat tart ütés alatt?

4. kérdés: A sakktáblán 5 bástya és néhány huszár áll úgy, hogy egyik bábu sem üti valamely másikat. Legfeljebb hány huszár van a táblán?

5. kérdés: Legkevesebb hány bástya és hány futó áll a sakktáblán, ha mindegyik bástya legalább két futót, illetve mindegyik futó legalább két bástyát támad, és ugyanannyi bástya van, mint futó?

Emma kérdésére egy újabb megoldás.

Egy bástya 4 irányban „lő”, és a tábla széleit összesen legfeljebb 32 lövés éri. Legyen a bástyák száma $\displaystyle x$.

Ha minden bástya két másikat tart ütés alatt, akkor 2 „lövése” éri a falat, így $\displaystyle 2x\le 32$ tehát a bástyák száma legfeljebb 16 lehet.

16 bástya elhelyezhető a táblán, lásd a 6. hozzászólást. A 16 bástyát elhelyezhetjük így is:

Köszönöm a fordulókhoz a linkeket, a feladatok/megoldások elérhetőségét.

Négy fordulóban is volt olyan feladat (9., 17., 24., 32. feladat), hogy bábukat pakolunk a sakktáblára, valamilyen szabályt betartva, minél többet. Ezek a sakktáblás feladatok segíthetnek új kérdéseket megfogalmazni. A 17-es meglepő módon azonos a gyomos feladattal (lásd F.3220, KöMaL), és ez egy különleges, érdekes feladat, feladatkör.

A 28-as feladathoz sokféle indoklás érkezett, szép ötletekkel, kisebb hiányosságokkal. Ezekről is lehetne itt a Fórumban beszélgetni. (Lásd még: F.2280, P.364, KöMaL)

A 23-asra érkezett egy káprázatos, 8 oldalas megoldás, ez cikk lehetne a KöMaL-ban. (Az általános eset vizsgálata közben bizonyítja az 1997-es IMO 6. feladatát.) Ebből a megoldásból sokat tanulhatunk, ..., ha láthatjuk. Ezt lehetővé teheti a Fórum.

Szándékunk, hogy a kitűzött feladatok megoldására egy érdeklődő tizenévesnek hasonló esélye legyen, mint egy nyugdíjas matematikatanárnak. (Vannak is beküldők mindkét csoportból.)

Évente négyszer jelenik meg új feladatsor, 2 hetes beküldési határidővel. A Fórum lehetőséget ad az aktivitásra a köztes időszakokban.

(Ha a Fórumban hosszabb ideig csend van, akkor követem a 2.hsz. tanácsát: "Javaslom, dobj be egy-egy konkrét feladatot, amit meg tudunk tárgyalni.")

Héttusa cikkek az érintőben: https://ematlap.hu/reszletes-kereso?szurtrovat=Héttusa

Moderátor, nem lehetne szétrobbantani ezt a témát kisebb témákra, minden fordulóra egy? És akkor a téma indítója tartalmazhatja a feladatokat is.

hsz 3-9,12-14 : 5. forduló

hsz 10,11,15,17 : nem héttusa

hsz 16 : 3. forduló

Feleltessünk meg a kártyáknak 3-dimenziós rácspontokat. A feladat olyan $\displaystyle P,Q$ pontpárokat elkerülni, amelyekre $\displaystyle PQ$ párhuzamos egy koordináta­síkkal, de nem párhuzamos egyik tengellyel sem. Úgy is fogalmazhatunk, hogy a rossz pontpár azonos rétegben van, de nincs egy vonalban (az ,,egy vonalban" kifejezés pontosan a Makay Géza által bevezetett blokk fogalmat jelenti).

Lássuk be teljes indukcióval, hogy az $\displaystyle [n]\times [m]\times [h]$ ($\displaystyle n,m,h\ge4$) rácstéglában legfeljebb $\displaystyle n+m+h-6$ pont vehető fel úgy, hogy ne legyen köztük rossz pontpár. Nézzük először a 4x4x4-es kockát, abban is a vízszintes ($\displaystyle z=k, k=1..4$) rétegeket. Tegyük fel, hogy van 7 pont a kockában, rossz pár nélkül.

$\displaystyle \bullet$ Ha valamelyik rétegben 4 pont van, azok szükségképpen egy vonalban vannak, így minden $\displaystyle x,y$ értékpárt lefednek, tehát egy további pont akármelyik rétegben ezek egyikével rossz párt alkotna.

$\displaystyle \bullet$ Ha valamelyik rétegben 3 pont van – szükségképpen egy vonalban – akkor ebben a vonalban egy pont hiányzik, és minden további (tehát 4) pont a hiányzó $\displaystyle x$ vagy $\displaystyle y$ koordinátaértékhez tartozó, a vonalra merőleges függőleges rétegbe kell hogy essen, ami az előbbi miatt rossz párhoz vezet.

$\displaystyle \bullet$ Végül, ha csak 3 vízszintes rétegben lenne pont, akkor valamelyik rétegbe legalább 3 pont jutna a 7-ből. Ez tehát nem lehet, és így feltehetjük, hogy mind a 4 rétegben van pont, méghozzá 2-2-2-1 elosztásban.

Legyenek ezeknek a vetületei a $\displaystyle z=0$ síkon $\displaystyle A,A'$, $\displaystyle B,B'$, $\displaystyle C,C'$ és $\displaystyle D$. Könnyű látni, hogy $\displaystyle A$, $\displaystyle B$, $\displaystyle C$ és $\displaystyle D$ egy szabad bástyafelállásnak felel meg, azaz nincs közöttük kettő azonos vonalban, és nincs egybeesés sem, így ez a 4 pont minden $\displaystyle x,y$ értékpárt lefed, tehát pl. az $\displaystyle A'$-nek megfelelő pont valamelyik vesszőtlen pont ősével rossz párt kell hogy alkosson. Ez pedig ellentmondás.

Tehát a 4x4x4-es kockában legfeljebb 6 megfelelő pont lehet. (Annyit meg is lehet adni, méghozzá különös módon kétféleképpen, amikor 3+3, illetve amikor 2+2+2 esik egy-egy kitérő vonalba.)

Az $\displaystyle n+m+h$ szerinti teljes indukciós lépés nagyon egyszerű. Tekintsük a $\displaystyle n,m,h$ közül a legnagyobbnak megfelelő irányt függőlegesnek. Ha így minden vízszintes rétegben legalább 2 pont van, akkor a párok vetületeiről ugyanazt mondhatnánk, mint a 4x4x4-es bizonyítás végén. Ezért valamelyik vízszintes rétegben legfeljebb 1 pont van, ezt a réteget elhagyva, alkalmazhatjuk az indukciós feltevést az eggyel kisebb téglára, és készen vagyunk.

A 21. feladatra a válaszom nem 32, hanem 720 volt, és azt kis vita után elfogadták.

Ugyanis ha Hófehérke lefelé fordított névjegykártyákkal jelölte meg a helyeket, és azokat csak a törpék Kuka mögötti felsorakozása után fedi fel, akkor bármilyen ülésrend kialakulhat.

1. állítás: A feltételeknek megfelelő kiválasztott lapok mindenképpen "blokkokba" rendezhetőek: egy blokkon belül két tulajdonság fog megegyezni minden kártyán, a blokkok között pedig egy sem.

Bizonyítás: Legyen két kártyán két tulajdonság megegyező, a korábbi jelöléssel a két kártya legyen ABC és ABD (itt most a törpe az A, a sapka a B, és a szerszám a C és a D). Egy harmadik kártya legyen EFG. Ha ez a kártya semmiben nem egyezik meg a másik kettővel, akkor másik blokkban van. Ha $\displaystyle E=A$, akkor lehet $\displaystyle F=B$, és akkor a kártya a két másikkal azonos blokkban van. Ha $\displaystyle E=A$ és $\displaystyle F\not =B$, akkor lehetne még $\displaystyle C=G$, de akkor az ABD és az EFG kártyák csak egy tulajdonságban egyeznek. Hasonlóan látható, hogy $\displaystyle D=G$ sem lehet, és az $\displaystyle A\not =E$, $\displaystyle B=F$ sem fordulhat elő.

2. állítás: A probléma megoldható legfeljebb 3 blokkal is.

Bizonyítás: Ha példaul a törpe és a sapka egyezik meg két különböző blokkon belül, akkor az a két blokk összevonható lenne egybe is úgy, hogy ugyanaz a törpe és sapka legyen mindkét blokk kártyáin. Ugyanis ha a blokkok között nincs egyezés, akkor a két blokk egy blokkba olvasztásával sem lesz egyezés, és az eddig "diszjunkt" két blokkból pedig egy szabályos blokk lesz. Ezt az eljárást bármelyik tulajdonságpárra elvégezhetjük, így a blokkok számát a tulajdonságpárok száma felülről korlátozza, az pedig 3.

3. állítás: Ha egy blokk van, akkor legfeljebb 7 kártyát választhatunk ki.

Bizonyítás: Mivel két tulajdonság rögzített a blokkon belül, csak a harmadik változhat, és a tulajdonságok közül a törpéből van legtöbb, így legfeljebb 7 kartya lehet a blokkban.

4. állítás: Ha két blokk van, akkor legfeljebb 11 kártyát választhatunk ki.

Bizonyítás: Egy a törpékben különböző blokkban maximum 7 kártya lehet, de ha két blokk van és azok egyetlen tulajdonságban sem egyeznek meg, akkor egy törpét a másik blokk számára kell fenntartanunk, így a blokkban már csak 6 kártya lehet. Hasonló okoskodással a sapkában különböző blokkban csak 6 kártya lehetne, de abból is egyet a másik blokkban kell használnunk, úgy már csak 5 kártya lehet a blokkban, ez összesen 11 kártya. És ilyen kártya húzás lehetséges: 111, 211, 311, 411, 511, 611, 722, 732, 742, 752, 762.

5. állítás: Ha három blokk van, akkor legfeljebb 12 kártyát választhatunk ki.

Bizonyítás: A fenti okoskodást tovább gondolva a törpékben különböző blokkban legfeljebb 5 kártya lehet (két törpét "használunk el" a másik két blokkban), a sapkás blokkban 4 kártya lehet, a szerszámosban pedig 3. Ez összesen 12, és a programom megtalálta ezt a megoldást, de ez alapján akár fejben is megoldható lett volna a feladat. Nekem viszont kellett a számítógép által adott megoldásból származó sejtés... :)

Elnézést, hogy értetlenkedek, de ebből számomra még az sem derül ki, hogy a saroknégyzetbeli piros mezőknek két átellenes lapon kellene lenniük, nemhogy az, hogy a pirosaknak két átellenes lap átlójában kell lenniük. Lemaradtam valamiről, kihagytam valamit?

Lehet, hogy félreértettem, de a bejegyzésed azt sugallja, mintha nem lenne más lehetőség, mint hogy a bástyák egy körben vannak, vagy négy körben vannak. Csak a tisztázás kedvéért: a bástyák alkothatnak kettő vagy három kört is, könnyű ilyet konstruálni pl. úgy, hogy a főátló mentén megfelelő méretű négyzet alakú táblarészekben csinálunk egy-egy kört.