| [44] Káli gúla | 2024-07-16 16:55:56 |
 Érdemes úgy elképzelni, hogy (1) ez egy kétszemélyes játék, (2) a bank tudja, hogy milyen kártyák vannak a bácsi kezében, (3) a bank nem akar 30 ezernél több pénzt kifizetni. Lehet-e ebben a játékban nyerni a bankkal szemben?
|
|
| [43] Keresztvölgyi József | 2024-07-16 14:20:26 |
 A 7. kérdésre adott válaszom (34 ezer dollár) csak becslés. Lehet, hogy csak 33 ezer dollár.
Ha Dagobert bácsi mindegyik bankkártyájával 5 ezer dollárt igényel, akkor 30 ezret kap. Ugyanígy ha mindig 6 ezret igényel, akkor is 30 ezerhez juthat hozzá.
Viszont taktitázhat úgy, hogy a már megtörtént lehívásai összegeinek és sikerességeinek függvényében módosítgatja az igénylendő összeget. Ezáltal a 30 ezernél többhöz is hozzájuthat.
Véleményem szerint egy ügyes programozó tudna írni egy olyan programot, amely még elfogadható (polinomális) idő múlva megadná a választ.
|
| Előzmény: [41] Róka Sándor, 2024-07-14 22:22:50 |
|
|
| [41] Róka Sándor | 2024-07-14 22:22:50 |
 Két új kérdés.
6. kérdés: Legfeljebb hány királynő helyezhető el a sakktáblán úgy, hogy mindegyik legfeljebb egy másikat tartson ütés alatt?
7. kérdés: Dagobert bácsinak van 10 bankkártyája, melyeken 1, 2, 3, ..., 10 ezer dollár van. Szegény már elfelejtette, hogy ezek melyik kártyán vannak, csak a pénzösszegekre emlékszik. Mindegyik kártya csak egyszer használható. Dagobert bedughatja a kártyát az ATM-be, és kérhet valamilyen összeget. Ha van rá fedezet, az ATM kiadja a kért pénzösszeget, különben nem ad ki semmit. Sajnos az ATM nem mutatja meg, hogy mennyi pénz volt a kártyán. Mekkora az a legnagyobb összeg, amit Dagobert bácsi biztosan fel tud venni a kártyákról?
|
| Előzmény: [22] Róka Sándor, 2024-07-07 09:17:06 |
|
| [40] Makay Géza | 2024-07-14 19:01:17 |
 Most írom a 4. kérdésre a választ... :)
Az 5 bástya lefog 5 sort és 5 oszlopot a táblából. 3 sor és 3 oszlop marad szabad, ahová egyáltalán el lehet helyezni huszárt. Így legfeljebb 3×3=9 huszárt lehet elhelyezni, az pedig lehetséges is:
|
 |
| Előzmény: [22] Róka Sándor, 2024-07-07 09:17:06 |
|
|
| [38] Makay Géza | 2024-07-14 13:53:58 |
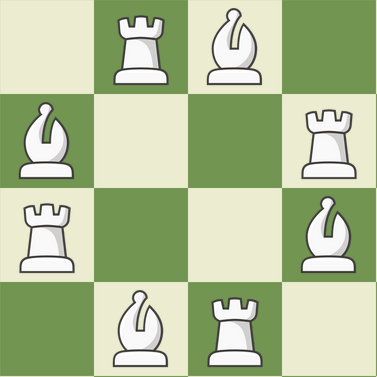
 4. kérdés. Mivel a bástya által ütött két futó nem lehet ugyanaz a két futó, ami üti a bástyát, ezért legalább 4 futó van. A szerepeket felcserélve is okoskodhatnánk, de mivel ugyanannyi bástya és futó van, ezért legalább négy bástyának is lennie kell. És erre itt egy lehetséges elhelyezés:
|
 |
| Előzmény: [22] Róka Sándor, 2024-07-07 09:17:06 |
|
| [37] Makay Géza | 2024-07-14 12:45:03 |
 Ez alapján 3 "szabad" rácspontunk van, amit nem muszáj lefednünk. Így nem lehet minden sarok üres, mert az 4 nem lefedett rácspontot jelentene. Nem lehet mind a 4 sarokban egymást átlósan ütő király-pár, mert az is 4 plusz rácspontot igényelne. 0 vagy 2 olyan király lehet, amelyik nem üt másikat, hiszen egy király önmagában 4 rácspontot foglal el. Ezek alapján kell legyen egy olyan sarok, amelyben két király oldalszomszédos mezőn áll. Forgatással és tükrözéssel megoldható, hogy ezek a bal felső sarokban az első sorban álljanak. Ha ehhez hozzávenném, hogy nyilvántartsam a "kihagyott" rácspontokat, akkor a program valószínűleg záros határidőn belül lefutna.
Másik ötlet a fentiek alapján, hogy a király-párokat igyekszem lerakni. Alapvetően nem sok eset lehet:
1. Minden pár oldalszomszédos: 3 rácspont marad ki.
2. Két egyedülálló király van (mint pl. a 27-es hozzászólásban), a többi oldalszomszédos: 1 rácspont marad ki.
3. Két egyedülálló király van, egy átlósan ütő pár, a többi oldalszomszédos: nincs kimaradó rácspont.
4. Egy, kettő vagy három átlósan ütő pár van, a többi oldalszomszédos: 2, 1 vagy 0 rácspont marad ki.
Mivel főleg király-párokat helyezünk el, a vizsgálandó esetek száma óriásit csökken, ez szerintem másodperceken belül meg kell adja az összes megoldást, bár leprogramozni bonyolultabb (valakinek nincs kedve megcsinálni? :) ). Amúgy szerintem a 3. pont és a 4. pontból az utolsó kettő nem fog előfordulni.
|
| Előzmény: [34] Róka Sándor, 2024-07-13 20:54:06 |
|
| [36] Makay Géza | 2024-07-14 12:06:32 |
 Kiszűrtem a forgatással/tükrözéssel egymásból megkapható megoldásokat és pár perc futás után találtam 156 megoldást. A programom nem nézte végig (valószínűleg ebben a formában nem is tudja végignézni) az összes lehetséges megoldást, így nem tudom, hogy ez mennyire van "közel" az összeshez...
|
| Előzmény: [29] sakkmath, 2024-07-12 22:14:03 |
|
|
| [34] Róka Sándor | 2024-07-13 20:54:06 |
 Miért nem lehet 26-nál több királyt elhelyezni a táblán?
Figyeljük az "elfoglalt" rácspontokat.
A sakktáblán a rácsegyenesek 9⋅9=81 pontban metszik egymást, 81 rácspont van.
2 egymást ütő király 6 vagy 7 rácspontot foglal el. Ha 2 másik ilyen királyt nézünk, azokhoz más rácspontok tartoznak. Ha a 26 király 13 párt alkot (az egy párban lévők ütik egymást), akkor ők legalább 13⋅6=78 rácspontot foglalnak el a 81-ből ...
|
| Előzmény: [24] Makay Géza, 2024-07-12 12:02:14 |
|
|
|
|
|
| [29] sakkmath | 2024-07-12 22:14:03 |
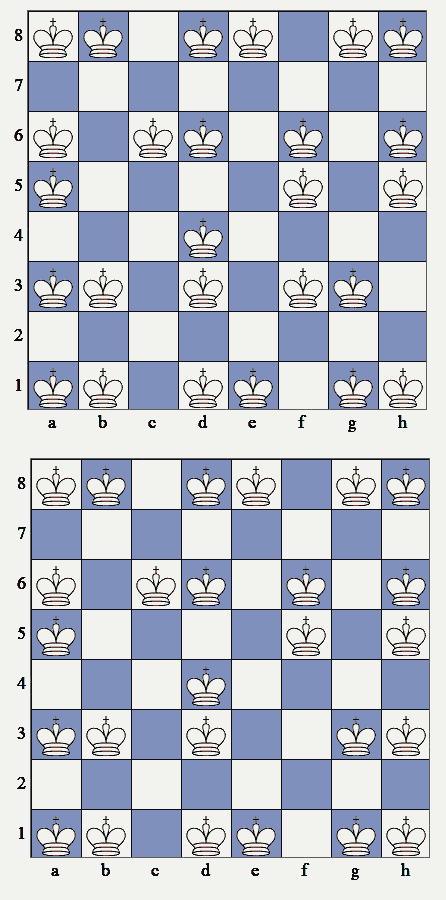
 Újabb két megoldás alul.
24/b. feladat:
Hány különböző megoldása van a feladatnak, ha eltekintünk a (tengelyes-, vagy középpontos) tükrözésekből adódó többletmegoldásoktól?
|
 |
| Előzmény: [28] Káli gúla, 2024-07-12 21:42:47 |
|
| [28] Káli gúla | 2024-07-12 21:42:47 |
 De talán ez a legjobb, mert a mintázat könnyen bővíthető minden 6k+2 oldalú táblára. Sőt, minden páros n-ről (n+6)-ra.
|
 |
|
|
| [26] S.Ákos | 2024-07-12 20:52:34 |
 Szerintem erre gondolt a kolto:
Ka1,Kb1,Kd1,Ke1,Kg1,Kh1,
Ka3,Kb3,Kd3,Ke3,Kg3,Kh3,
Ka5,Kb5,Kd5,Ke5,Kg5,Kh5,
Ka7,Ka8,Kc7,Kc8,Kf7,Kf8,Kh7,Kh8
|
 |
| Előzmény: [25] sakkmath, 2024-07-12 19:09:27 |
|
| [25] sakkmath | 2024-07-12 19:09:27 |
 Soraidból sajnos nem tudom egyértelműen beazonosítani a programod megoldását/megoldásait. Örülnék, ha ezt/ezeket vagy ábrán, vagy koordinátázva bemutatnád, vagy leírnád.
|
| Előzmény: [24] Makay Géza, 2024-07-12 12:02:14 |
|
|
| [23] Káli gúla | 2024-07-07 10:40:44 |
 A lövős analógia a futókra is használható. A sarkokat ferdén levágjuk, így lesz 28 falszakasz. A többi szélső mezőről (24) legalább 1 falszakasz látható, a többi mezőről már 4-felé lehet lőni, ami már bábunként 2-2 új falszakaszt jelent. És a 4 sarokfalat lehet is támadni 1-1 átlómezőről.
|
 |
| Előzmény: [21] Róka Sándor, 2024-07-06 20:40:30 |
|
| [22] Róka Sándor | 2024-07-07 09:17:06 |
 Újabb kérdések:
3. kérdés: Legfeljebb hány király állhat a sakktáblán, ha mindegyik legfeljebb egy másikat tart ütés alatt?
4. kérdés: A sakktáblán 5 bástya és néhány huszár áll úgy, hogy egyik bábu sem üti valamely másikat. Legfeljebb hány huszár van a táblán?
5. kérdés: Legkevesebb hány bástya és hány futó áll a sakktáblán, ha mindegyik bástya legalább két futót, illetve mindegyik futó legalább két bástyát támad, és ugyanannyi bástya van, mint futó?
|
| Előzmény: [3] Róka Sándor, 2024-07-02 14:04:12 |
|
| [21] Róka Sándor | 2024-07-06 20:40:30 |
 Emma kérdésére egy újabb megoldás.
Egy bástya 4 irányban „lő”, és a tábla széleit összesen legfeljebb 32 lövés éri. Legyen a bástyák száma x.
Ha minden bástya két másikat tart ütés alatt, akkor 2 „lövése” éri a falat, így 2x≤32 tehát a bástyák száma legfeljebb 16 lehet.
16 bástya elhelyezhető a táblán, lásd a 6. hozzászólást. A 16 bástyát elhelyezhetjük így is:
|
 |
| Előzmény: [7] UdvariTibor, 2024-07-02 18:23:50 |
|
| [20] Róka Sándor | 2024-07-05 17:40:24 |
 Köszönöm a fordulókhoz a linkeket, a feladatok/megoldások elérhetőségét.
Négy fordulóban is volt olyan feladat (9., 17., 24., 32. feladat), hogy bábukat pakolunk a sakktáblára, valamilyen szabályt betartva, minél többet. Ezek a sakktáblás feladatok segíthetnek új kérdéseket megfogalmazni. A 17-es meglepő módon azonos a gyomos feladattal (lásd F.3220, KöMaL), és ez egy különleges, érdekes feladat, feladatkör.
A 28-as feladathoz sokféle indoklás érkezett, szép ötletekkel, kisebb hiányosságokkal. Ezekről is lehetne itt a Fórumban beszélgetni. (Lásd még: F.2280, P.364, KöMaL)
A 23-asra érkezett egy káprázatos, 8 oldalas megoldás, ez cikk lehetne a KöMaL-ban. (Az általános eset vizsgálata közben bizonyítja az 1997-es IMO 6. feladatát.) Ebből a megoldásból sokat tanulhatunk, ..., ha láthatjuk. Ezt lehetővé teheti a Fórum.
Szándékunk, hogy a kitűzött feladatok megoldására egy érdeklődő tizenévesnek hasonló esélye legyen, mint egy nyugdíjas matematikatanárnak. (Vannak is beküldők mindkét csoportból.)
Évente négyszer jelenik meg új feladatsor, 2 hetes beküldési határidővel. A Fórum lehetőséget ad az aktivitásra a köztes időszakokban.
(Ha a Fórumban hosszabb ideig csend van, akkor követem a 2.hsz. tanácsát: "Javaslom, dobj be egy-egy konkrét feladatot, amit meg tudunk tárgyalni.")
|
| Előzmény: [19] Sinobi, 2024-07-05 11:20:33 |
|
